The New Turing Omnibus Chapter 5 Gödel's Theorem

We began by discussing the "Big Picture" from Tom's notes, focussing on the ideas of David Hilbert in 1920 to formulate mathematics on a solid and complete logical foundation.

With this context in mind, we discussed how Kurt Gödel proved Hilbert's program was impossible and the possible ramifications of this discovery. We wondered how this related to the halting problem and Bertrand Russell and Alfred North Whitehead's idea of logicism.
We were careful to first understand that Gödel's findings (and Hilbert's ideas) were specifically about formal systems and James walked us through an example system from Douglas Hofstadter's "Gödel, Escher, Bach: an Eternal Golden Braid":

We discussed what it means for a formal system to be sound and what it means to be complete, using the aforementioned example pq- system to solidify our understanding.

We revisited the Predicate Calculus chapter to view it as a formal system and how it is both complete and sound.
With this in place, we then looked at arithmetic as a formal system and walked through a proof that 1 + 1 = 2 using the axioms given in the chapter.
With less than an hour remaining, we attempted to walk through Gödel's theorem, first discussing how every string can be encoded as a Gödel number and can therefore be subject to arithmetic itself. Chris demonstrated his Gödel number encoder/decoder:
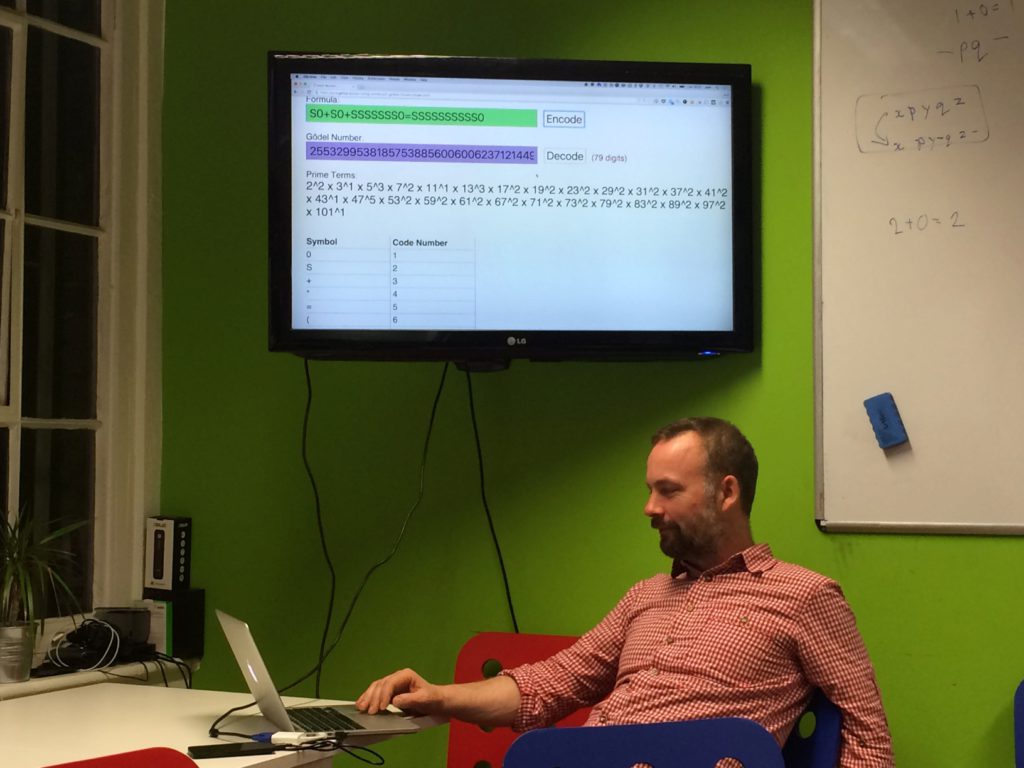
Joel uses Chris' Gödel number encoder/decoder
Finally: Tom led us through the rest of the theorem, explaining how any sufficiently powerful system (such as arithmetic) cannot be complete as it will always be able to express a string that cannot be proven but is true.
- There was general consensus that this was one of the most difficult chapters we've encountered so far and greatly appreciated Tom's preparation;
- We discussed the possibility that this topic might have been better spread over several meetings but how this was at odds with our desire to keep each meeting self-contained (in an effort to attract more attendees);
- There was concern that the difficulty of this subject matter (and amount of mathematics) would scare away potential attendees;
- We reiterated our preference for having meeting shepherds (viz. at least one member of the group having read the chapter and done some preparation);
- Once more, we encouraged using material outside the book to aid discussion and to have meetings that aren't about The New Turing Omnibus at all.
Thanks to Daniel and Geckoboard for hosting, to Tom Stuart for shepherding, to James for his examples on the whiteboard and to Chris for his Gödel number generator.
- Home
- Documentation
- Choosing a Topic
- Shows & Tells
- Miscellaneous
- Opt Art
- Reinforcement Learning: An Introduction
- 10 Technical Papers Every Programmer Should Read (At Least Twice)
- 7 More Languages in 7 Weeks
- Lua, Day 1: The Call to Adventure
- Lua, Day 2: Tables All the Way Down
- Lua, Day 3
- Factor, Day 1: Stack On, Stack Off
- Factor, Day 2: Painting the Fence
- Factor, Day 3: Balancing on a Boat
- Elm, Day 1: Handling the Basics
- Elm, Day 2: The Elm Architecture
- Elm, Day 3: The Elm Architecture
- Elixir, Day 1: Laying a Great Foundation
- Elixir, Day 2: Controlling Mutations
- Elixir, Day 3: Spawning and Respawning
- Julia, Day 1: Resistance Is Futile
- Julia, Day 2: Getting Assimilated
- Julia, Day 3: Become One With Julia
- Minikanren, Days 1-3
- Minikanren, Einstein's Puzzle
- Idris Days 1-2
- Types and Programming Languages
- Chapter 1: Introduction
- Chapter 2: Mathematical Preliminaries
- Chapter 3: Untyped Arithmetic Expressions
- Chapter 4: An ML Implementation of Arithmetic Expressions
- Chapter 5: The Untyped Lambda-Calculus
- Chapters 6 & 7: De Bruijn Indices and an ML Implementation of the Lambda-Calculus
- Chapter 8: Typed Arithmetic Expressions
- Chapter 9: The Simply-Typed Lambda Calculus
- Chapter 10: An ML Implementation of Simple Types
- Chapter 11: Simple Extensions
- Chapter 11 Redux: Simple Extensions
- Chapter 13: References
- Chapter 14: Exceptions
- Chapter 15: Subtyping – Part 1
- Chapter 15: Subtyping – Part 2
- Chapter 16: The Metatheory of Subtyping
- Chapter 16: Implementation
- Chapter 18: Case Study: Imperative Objects
- Chapter 19: Case Study: Featherweight Java
- The New Turing Omnibus
- Errata
- Chapter 11: Search Trees
- Chapter 8: Random Numbers
- Chapter 35: Sequential Sorting
- Chapter 58: Predicate Calculus
- Chapter 27: Perceptrons
- Chapter 9: Mathematical Research
- Chapter 16: Genetic Algorithms
- Chapter 37: Public Key Cryptography
- Chapter 6: Game Trees
- Chapter 5: Gödel's Theorem
- Chapter 34: Satisfiability (also featuring: Sentient)
- Chapter 44: Cellular Automata
- Chapter 47: Storing Images
- Chapter 12: Error-Correcting Codes
- Chapter 32: The Fast Fourier Transform
- Chapter 36: Neural Networks That Learn
- Chapter 41: NP-Completeness
- Chapter 55: Iteration and Recursion
- Chapter 19: Computer Vision
- Chapter 61: Searching Strings
- Chapter 66: Church's Thesis
- Chapter 52: Text Compression
- Chapter 22: Minimum spanning tree
- Chapter 64: Logic Programming
- Chapter 60: Computer Viruses
- Show & Tell
- Elements of Computing Systems
- Archived pages