Capsule net tensorflow A simple tensorflow implementation of Capsnet on Hitton paper Dynamic Routing Between Capsules In the paper, Geoffrey Hinton introduces Capsule for:
A capsule is a group of neurons whose activity vector represents the instantiation parameters of a specific type of entity such as an object or object part. We use the length of the activity vector to represent the probability that the entity exists and its orientation to represent the instantiation paramters. Active capsules at one level make predictions, via transformation matrices, for the instantiation parameters of higher-level capsules. When multiple predictions agree, a higher level capsule becomes active.
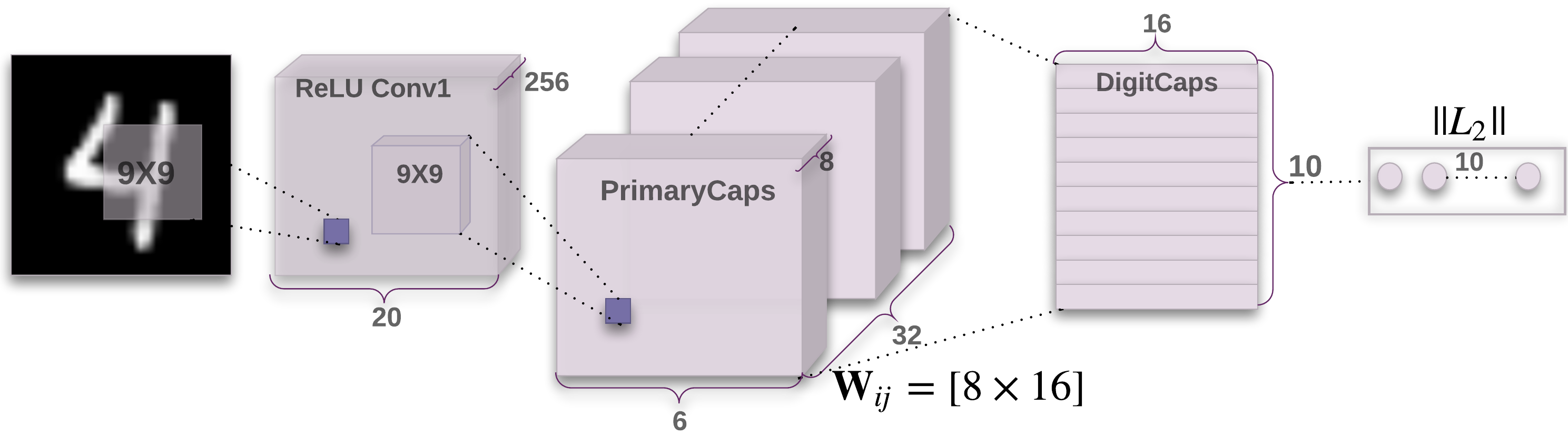 There are three key layer in capsnet.
There are three key layer in capsnet.
conv1 = tf.contrib.layers.conv2d(self.image, num_outputs=256, kernel_size=9, stride=1, padding='VALID')
input tensor size: [bathsize, 28, 28, 1], output tesnor size: [batchsize, 20, 20, 256]
input tensor size: [bathsize, 20, 20, 256], output tesnor size: [batchsize, 1152, 8, 1]
The detail of PrimaryCaps as follow:
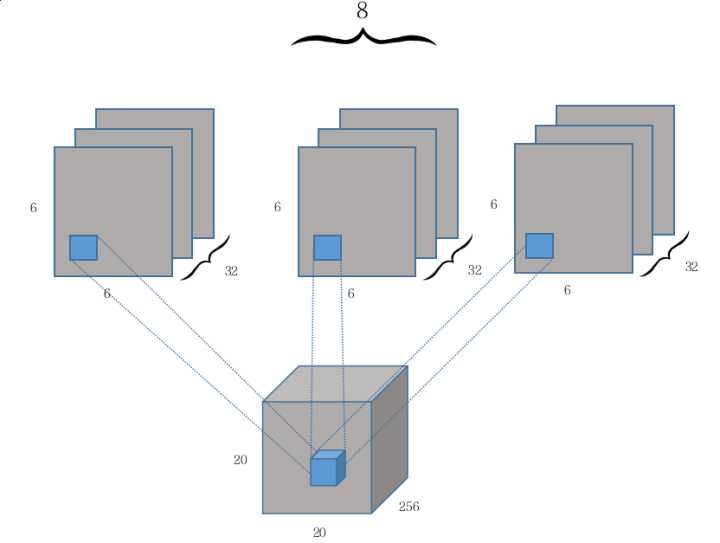
The primarycaps layer can be viewed as performing 8 Conv2d operations of different weights on an input
tensor of dimensions 20 x 20 x 256,
each time operation is a Conv2d with num_output=32, kernel_size=9, stride=2.
Since each convolution operation generates a 6 × 6 × 1 × 32 tensor and generates a total of 8 similar tensors,
the 8 tensors (that is, the 8 components of the Capsule input vector) combined dimensions become 6 × 6 × 8 × 32.
PrimaryCaps is equivalent to a normal depth of 32 convolution layer,
except that each layer from the previous scalar value into a length of 8 vector.
input tensor size: [batchsize, 1152, 8, 1], output tesnor size: [batch_size, 10, 16, 1]
The output of PrimaryCaps is 6x6x32=1152 Capsule units, and every Capasule unit is 8 length vector.
The DigitCaps has 10 standard Capsule units, each of the Capsule's output vectors has 16 elements.
In a word, DigitCaps rounting an updating based on the output vector of last layer.
The length of output vector is the probability of the class.
The length of the output vector of a capsule represents the probability that the entity represented by the capsule is present in the current input.
So its value must be between 0 and 1.
To achieve this compression and to complete the Capsule-level activation, Hinton used a non-linear function called "squashing."
This non-linear function ensures that the length of the short vector can be shortened to almost zero, while the length of the long vector is compressed to a value close to but not more than one.
The following is an expression of this non-linear function:

where v_j is the output vector of Capsule j, s_j is the weighted sum of all the Capsules output by the previous layer to the Capsule j of the current layer, simply saying that s_j is the input vector of Capsule j.
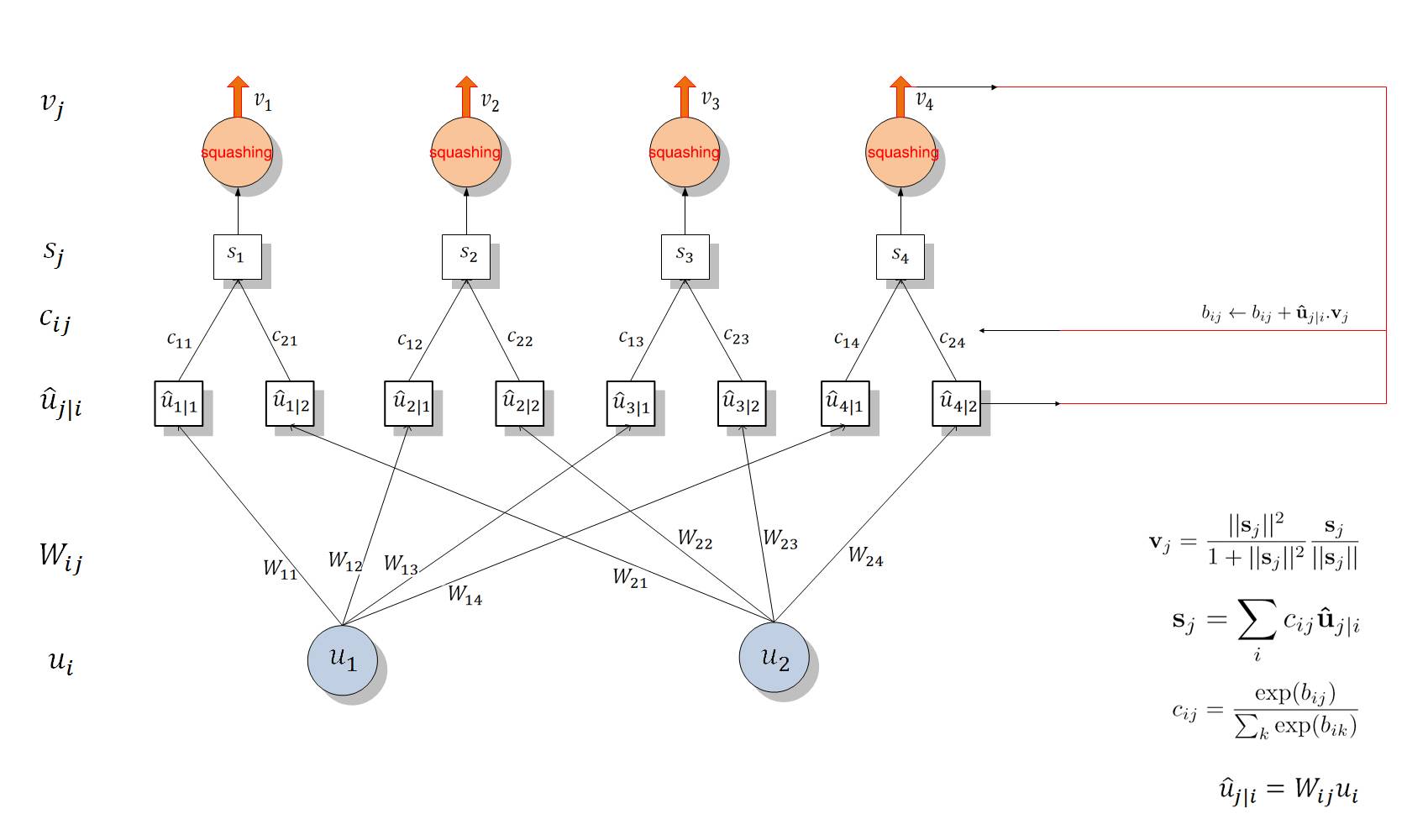
Since one Capsule unit is the 8D vector not like traditional scalar, how compute the vector inputs and outputs of capsule is the KEY.
Capsule's input vector is equivalent to the scalar input of a neuron in a classical neural network, which is equivalent to the propagation and connection between two Capsules.
The calculation of input vector is divided into two stages, namely linear combination and Routing, this process can be expressed by the following formula:

After determining u_ji hat, we need to use Routing to allocate the second stage to compute output node s_j, which involves iteratively updating c_ij using dynamic routing. Get the next level of Capsule's input s_j through Routing, and put s_j into the "Squashing" non-linear function to get the output of the next Capsule.
Routing algorithm as follow:

Therefore, the whole level of propagation and distribution can be divided into two parts, the first part is a linear combination of u_i and u_ji hat, the second part is the routing process between u_ji hat and s_j.
Dynamic routing is a kind of algorithm between the PrimaryCaps and DigitCaps to propagae "vevtor in vector output", propagation process as follow:
In the paper, the author used Margin loss which is commonly used in SVM. The expression of loss function is:
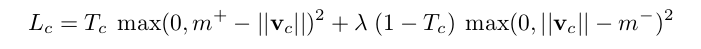
where T_c = 1 if a digit of class c is present and m_plus = 0.9 and m_minus = 0.1 and lambda = 0.5(suggest). The total loss is simply the sum of the losses of all digit capsules.
The paper used Reconstruction to regularization and improve accuracy.
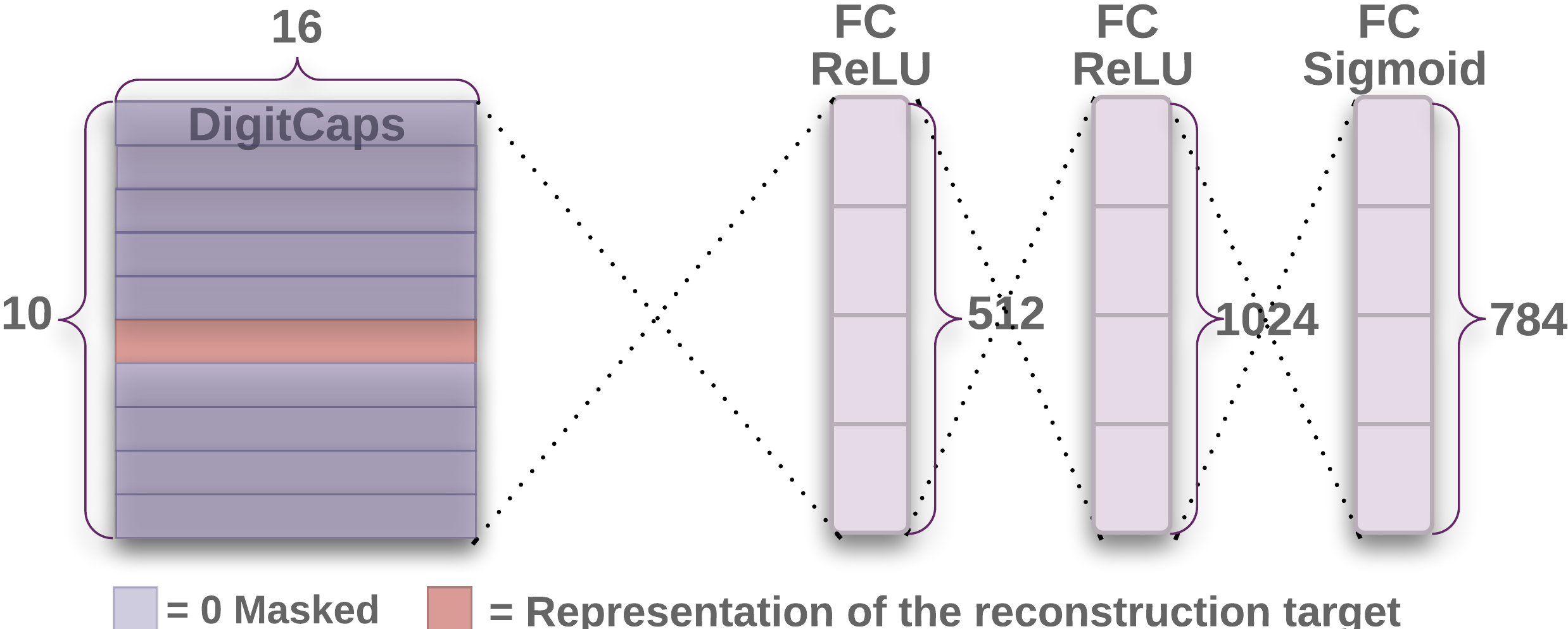
In addition to improving the accuracy of the model, Capsule's output vector reconstruction improve the interpretability of the model because we can modify the reconstruction of some or all of the components in the reconstructed vector and observe the reconstructed image changes which helps us to understand the output of the Capsule layer.
So, the total loss function is:
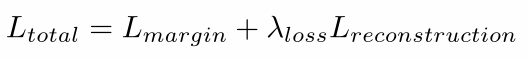
where, lambda_loss is 0.00005 so that it does not dominate the margin loss during training.
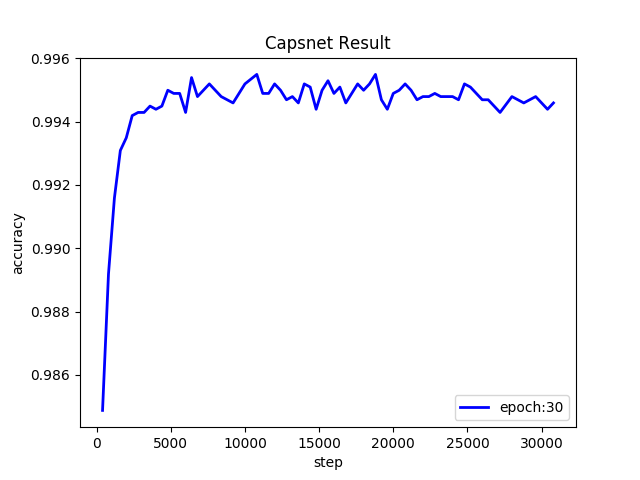
batchsize : 64
epoch: 30
train loss:
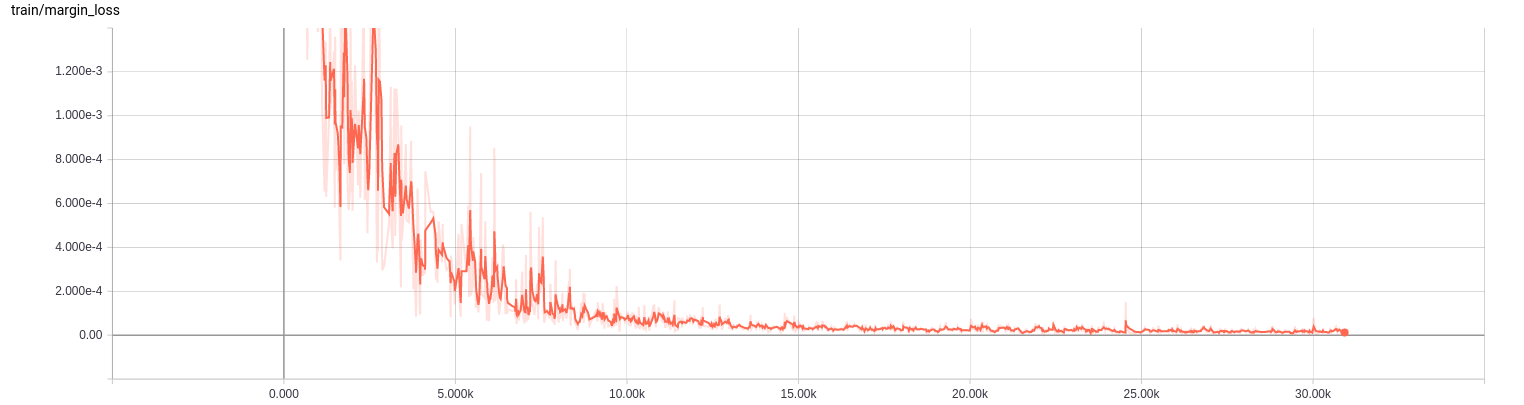

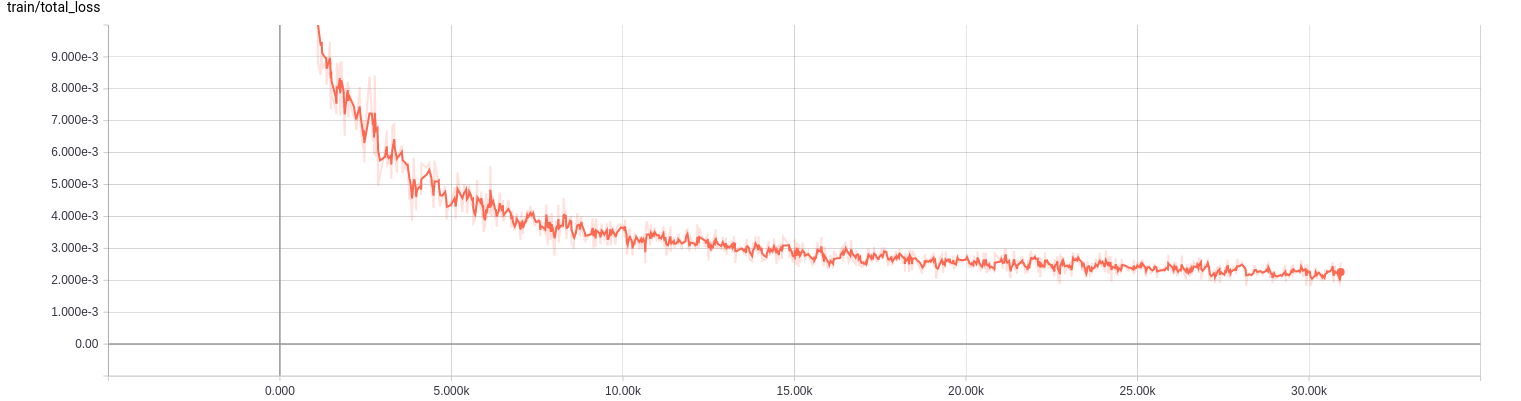
accuracy:
- Capsnet on fashion-mnist
- Capsnet on cifar10
- Modify network architecture
Reference:
https://www.jiqizhixin.com/articles/2017-11-05
https://github.com/naturomics/CapsNet-Tensorflow