I started this mainly for myself but for others to learn data structures and algorithms. We'll be diving in with Java, so sit back, enjoy, and feel free to follow along (you probably should).
Learning to code can be challenging. I remember feeling the need to know everything. You know what I mean - The Tutorial Hell Trap. And while a broad understanding is helpful, I often learned the most when diving into projects that intrigued me. However, it wasn't smooth sailing. In the beginning, I struggled because I didn't fully grasp the importance of DSA. Correction - I didn't know what DSA was. "Projects" after unfinished projects, I struggled to apply basic methods of programming.
Ever wondered about these situations?
- How do e-commerce applications quickly find a product by its ID? Could using hash tables be more efficient than arrays?
- Ever thought about how social networks like Facebook or LinkedIn manage user connections? What role do graph data structures and traversal algorithms play in finding mutual friends?
- Why do websites load faster on your second visit? Could this be due to efficient caching using doubly linked lists or hash maps?
You get the point. We'll explore various concepts, but remember, it's more about gradually mastering these concepts over time.
I guarantee making programs will be much more fun as you learn more concepts.
- Engage actively with the material. Don't just copy codes because that doesn't do ANYTHING for you; use ChatGPT / Google to challenge yourself with questions and ask for "real world" examples to apply DSA concepts. AI is a game-changer buddy.
- Remember, learning is a marathon, not a sprint. Set realistic goals and pace yourself. You'll be learning fast at first but don't expect to be learning 8 lessons a day. It's going to slow down so don't be disappointed. Even 1-2 concepts/day is FINE!
- Let's stop talking and start doing!
FYI: I'll be using VSCode on a Macbook (Apple Silicon chip).
- Introduction to Java
- Fundamentals of Data Structures
- Basic Algorithms
- Intermediate Data Structures
- Advanced Sorting Algorithms
- Advanced Concepts
I chose Java because of its unique balance between performance and usability. Unlike C, Java offers a more forgiving and intuitive programming environment, which is excellent for beginners. But honestly, I'm using Java because I wanna. You think it's a joke, huh?
- Download Java/JDK: Visit the Official Java Website to download the Java Development Kit (JDK).
Think of Java like the ABCs of computer language. It's what we use to tell the computer what to do. The JDK? That's your toolbox. It has all the tools (like a compiler and libraries) you need to start creating with Java.
-
Begin by confirming your current directory in Visual Studio Code. This can be done by opening the terminal (View > Terminal) and typing the command
pwdto display your current directory.>> pwd
-
If the displayed directory is where you want your Java file to be located, you can move to the next step.
-
If you want to change your directory, use the
cdcommand followed by the path to your preferred directory.>> cd ../../path-to-your-preferred-directory
-
-
In your directory, initiate a new Java file named
HelloWorld.java. You can use thecodecommand, which opens the file in a new Visual Studio Code tab.>> code HelloWorld.java -
Once
HelloWorld.javais opened, input the following Java code then save(Cmd + S):// This is how you create a comment // Class Definition (*** make sure HelloWorld matches your file name HelloWorld.java ***) public class HelloWorld { // Main Method public static void main(String[] args) { System.out.println("Hello, World!"); } }
public class HelloWorldas the main label or title of your Java program, similar to how you name a document. It's like the cover of a book, telling you what's inside. In Java, every bit of code lives inside a class, so this is like naming your project.public static void main(String[] arg)is a "special tool" you are making in your Java toolkit. It's labeledpublic, meaning anyone can use it, andstaticmeans you can use it immediately, no special preparation needed. Thevoidindicates it won't return anything, like a tool used for a job but not for producing a direct output.
-
To run this script, either:
-
Click on the "Run Java" button (top right, resembles a play button).
-
Or, if you prefer using shell commands (recommended), make sure to save the file before running it:
>> java HelloWorld.java
You should see the output "Hello, World!".
-
Visit Learn Java Online for more Java Basics since I'll be covering DSA here, instead.
Alright, let's now dive in.
Data structures are fundamental in programming, transcending language barriers. While we'll focus on Java, the concepts apply universally. Once you grasp data structures, you can easily adapt this knowledge to other programming languages.
- Language-Independent Logic: Understanding data structures in one language eases their implementation in others, boosting your flexibility in diverse programming environments.
- Organization of Data: Data structures allow for systematic data organization and management, crucial for clean and efficient coding.
- Efficiency: The selection of the correct data structure can significantly improve algorithm performance since different structures excel in different tasks.
- Problem Solving: Knowledge of data structures aides in framing problems better, leading to more intuitive and clear solutions.
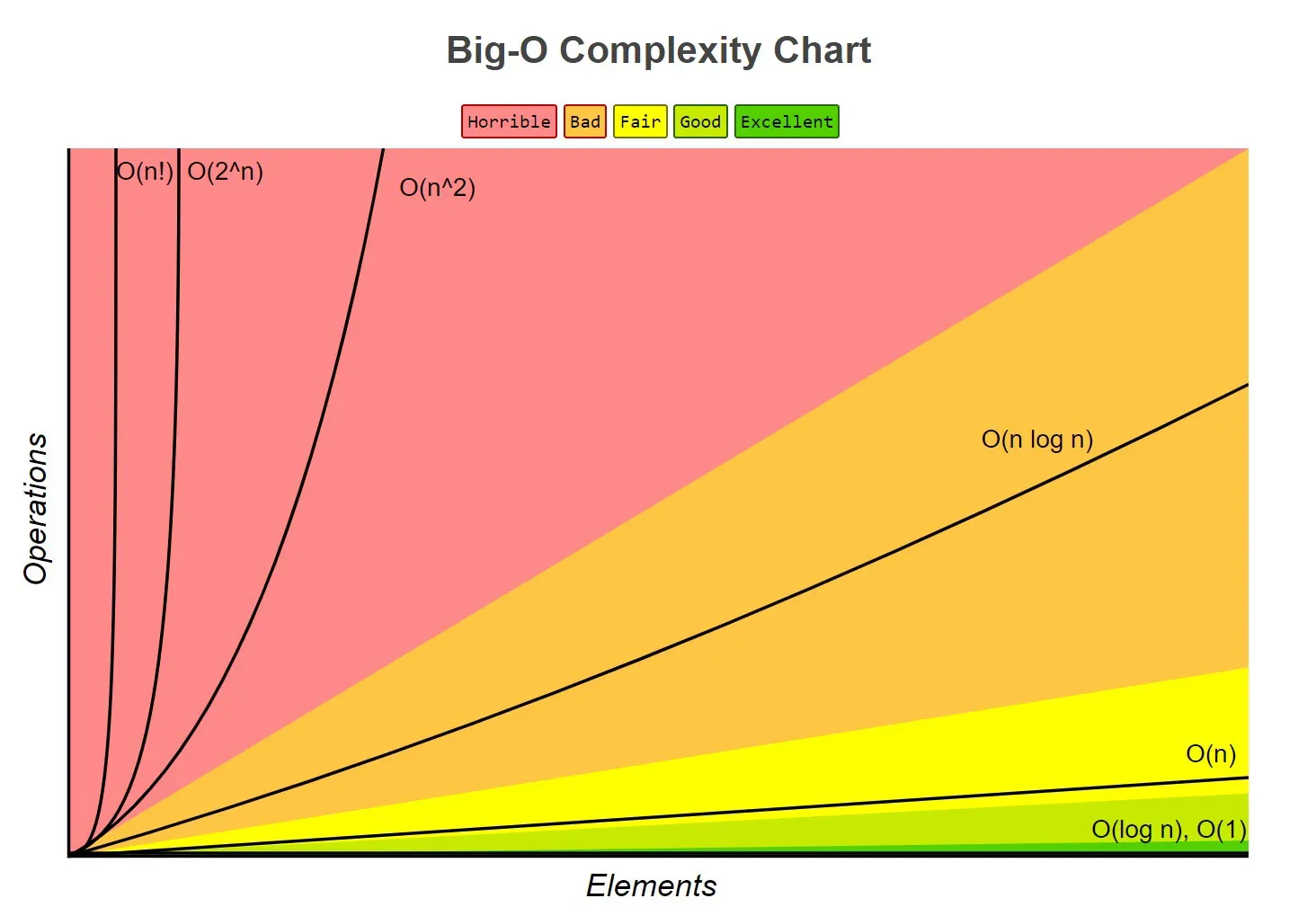
Before we dive into writing actual code, it's crucial for us to familiarize ourselves with Big O Notation. By understanding this concept, we can ensure that our codes are not only elegantly designed but also memory and processing efficient.
The efficiency of an algorithm often comes down to how its running time increases as we increase the input size, which is where the Big O notation comes into play. It gives us a high-level understanding of the time complexity of an algorithm.
Scenario 1: Nested Loop (O(n^2)) - A loop nested within another loop. This complexity suggests that the time taken doubles with each additional element.
Scenario 2: Two Separate Loops (O(n)) - Contrary to the first scenario, having two separate loops, each iterating over your data. This setup means that the runtime grows linearly and in direct proportion to the size of the input data set.
Quite clearly, using two separate loops would provide a faster runtime.
To summarize, here are different types of logical complexities represented by Big O notation:
- Logarithmic algorithm – O(log n): Runtime grows logarithmically with n.
- Linear algorithm – O(n): Runtime grows in direct proportion to n.
- Superlinear algorithm – O(n log n): Runtime grows in proportion to n but slightly faster due to the additional log n factor.
- Polynomial algorithm – O(n^c): Runtime grows at a rate of n raised to the power of any constant c.
- Exponential algorithm – O(c^n): Runtime grows exponentially with n, and doubles with each addition to the input data set.
- Factorial algorithm – O(n!): Runtime grows the fastest and can quickly become unusable for even small values of n.
Arrays in Java are a fundamental data structure characterized by the following key features:
- Contiguous Memory: Arrays store elements next to each other, allowing effective element access and manipulation.
- Fixed Size: The count of elements an array can store is set upon creation and can't change.
- Homogeneity: All elements in an array share the same data type.
- Direct Access: Arrays use indices to provide immediate access to elements, which speeds up read operations.
- Efficient Storage: Arrays are compact and suitable for storing large sets of similar data, optimizing memory use.
Here's an example:
class ArrayExample {
public static void main(String[] args) {
// Declare array of integers then allocate memory for 10 integers
int[] Array;
Array = new int[10];
// Initialize first element[0] then second element[1] and so on...
Array[0] = 100;
Array[1] = 200;
Array[2] = 300;
Array[3] = 400;
Array[4] = 500;
Array[5] = 600;
Array[6] = 700;
Array[7] = 800;
Array[8] = 900;
Array[9] = 1000;
// Print
System.out.println("Element at index 0: " + Array[0]);
System.out.println("Element at index 1: " + Array[1]);
System.out.println("Element at index 2: " + Array[2]);
System.out.println("Element at index 3: " + Array[3]);
System.out.println("Element at index 4: " + Array[4]);
System.out.println("Element at index 5: " + Array[5]);
System.out.println("Element at index 6: " + Array[6]);
System.out.println("Element at index 7: " + Array[7]);
System.out.println("Element at index 8: " + Array[8]);
System.out.println("Element at index 9: " + Array[9]);
}
}Output:
Element at index 0: 100
Element at index 1: 200
Element at index 2: 300
Element at index 3: 400
Element at index 4: 500
Element at index 5: 600
Element at index 6: 700
Element at index 7: 800
Element at index 8: 900
Element at index 9: 1000
However, this current code is a bit inefficient and unnecessarily cluttered. We could avoid wasting time and tidy up our code by refraining from writing repetitive lines. This brings us to our next valuable lesson - Loops.
Mastering loops is fundamental to efficient programming. They save time by handling repetitive tasks flexibly, eliminating the need for extensive, redundant code. We'll briefly explore two common types of loops here:
- For Loops: Efficient for iterating a known number of times.
- While Loops: Useful when the number of iterations is not predetermined.
Do some digging on loops when you get a chance; there's quite a few variations out there: Do-While Loops, Infinite Loops, Loops with 'else' clauses, Comprehension Loops, Iterator Loops, Generator Loops, Nested Loops, and more. The rabbit hole goes deep so have fun exploring.
Now, coming to the examples:
Make your 'ArrayExample' class and driver code. This will initialize and interact with an array. I've prepared an integer array with ten slots reserved, and in the commented section, 'Insert Loop codes here'.
public class ArrayExample {
public static void main(String[] args) {
int[] Array;
Array = new int[10];
// <Delete entire line; copy/paste loop here>
}
}// Initializes each element to a multiple of 100 and then print its index and value
for (int i = 0; i < Array.length; i++) {
Array[i] = (i + 1) * 100;
System.out.println("Element at index "+i+": "+Array[i]);
}// Populate each element with a multiple of 100 and display its index and value
int i = 0;
while (i < Array.length) {
Array[i] = (i+1) * 100;
System.out.println("Element at index "+i+": "+Array[i]);
i++;
}Both Outputs:
Element at index 0: 100
Element at index 1: 200
Element at index 2: 300
Element at index 3: 400
Element at index 4: 500
Element at index 5: 600
Element at index 6: 700
Element at index 7: 800
Element at index 8: 900
Element at index 9: 1000
Although arrays are powerful in their simplicity and direct access, they come with limitations, particularly in their fixed size and the complexity involved in inserting or deleting elements. To address these limitations, let's explore another fundamental data structure: Linked Lists.
Linked Lists, as dynamic data structures, differ significantly from arrays. Key highlights include:
- Dynamic Size: They can expand or contract, offering flexibility.
- Easy Modifications: Insertions and deletions are simpler, without needing to shift other elements.
- Non-Contiguous Storage: Elements ('nodes') are linked via pointers and can reside anywhere in memory.
On the flip side:
- Increased Memory: Nodes consume extra memory due to data and pointer storage.
- Sequential Access: Direct element access is not possible; traversal from the start is required.
So, we've looked at the characteristics of linked lists, but what does this all mean in practice? Imagine a toy train set.
Arrays are like a train with tightly coupled cars. Adding or removing cars (or elements) in the middle is a pain in the butt - you have to disconnect and move all subsequent cars. It's efficient when working with data en masse, but individual modifications can be taxing.
Before Insertion:
+---+---+---+---+
| A | B | C | D |
+---+---+---+---+
Inserting 'X' at index 2:
+---+---+---+---+---+
| A | B | X | C | D |
+---+---+---+---+---+
→
Elements shifted right
Before Deletion:
+---+---+---+---+
| A | B | C | D |
+---+---+---+---+
Deleting 'B':
+---+---+---+
| A | C | D |
+---+---+---+
←
Elements shifted left
Linked Lists, on the other hand, function like a train with easily detachable cars. Each car (or Node) hooks onto the next, allowing us to seamlessly insert or remove cars in the middle without disrupting the entire setup. This offers greater ease and efficiency when changing single elements, making Linked Lists a more flexible alternative for specific tasks.
Before Insertion:
+---+ +---+ +---+
| A | -> | B | -> | D |
+---+ +---+ +---+
Inserting 'C' after 'B':
+---+ +---+ +---+ +---+
| A | -> | B | -> | C | -> | D |
+---+ +---+ +---+ +---+
↑
Only pointers updated
Before Deletion:
+---+ +---+ +---+
| A | -> | B | -> | C |
+---+ +---+ +---+
Deleting 'B':
+---+ +---+
| A | ----------> | C |
+---+ +---+
↑
'B' is bypassed
This simplicity and flexibility are exactly why we use linked lists in programming when we expect to add or remove a lot of items.
So how do we create a linked list in Java? That's where Java's import java.util.* package comes in handy. It's like a toolbox full of helpful tools — and one of those tools is the LinkedList class. Instead of making your own gear, you just ask to use this. This saves you time, and you know it's going to work well because it’s been tried and tested.
I suggest you skimming through Package java.util to get a sense of the rich open-source resources at your disposal.
Anyways, let's get straight into Linked Lists:
// Skim, then practice. Make your own examples
// .add() = Add end
// .addFirst() = Add beginning
// .addLast() = Add last
// .add(2, "Pat") = Add specific
// .remove() = Remove first occurrence
// .remove(2) = Remove specific
// .removeFirst() = Remove first
// .removeLast() = Remove last
// .contains() = Contains an element
// .size() = Get size of list
// .isEmpty() = Check if empty
// .getFirst() = Get first non-empty element
import java.util.LinkedList;
public class LinkedListExample {
public static void main(String args[]) {
LinkedList<String> phoneBook = new LinkedList<String>();
phoneBook.add("Pat");
phoneBook.add("Charlie");
phoneBook.add("Sam");
phoneBook.addFirst("Alex");
phoneBook.addLast("Taylor");
phoneBook.add(4, "Pat");
System.out.println("List after additions: " + phoneBook);
phoneBook.remove("Pat");
phoneBook.remove(2);
phoneBook.removeFirst();
phoneBook.removeLast();
System.out.println("List after removals: " + phoneBook);
// More operations!!!
System.out.println("Contains Sam? " + phoneBook.contains("Sam"));
System.out.println("Get size of the list: " + phoneBook.size());
// First if statement practice
if (!phoneBook.isEmpty()) {
System.out.println("First in the list: " + phoneBook.getFirst());
}
phoneBook.clear();
System.out.println("List after clearing: " + phoneBook);
}
}Output in logical order:
List after additions: [Alex, Pat, Charlie, Sam, Pat, Taylor]
List after removals: [Charlie, Pat]
Contains Sam? false
Get size of the list: 2
First in the list: Charlie
List after clearing: []
Keep in mind, Linked Lists are good for implementing basic Searching Algorithms like Linear Search, but are not very efficient for Sorting Algorithms, since sorting algorithms require a lot of back-and-forth traversal and linked lists do not support indexing. However, linked lists are used in some recursive sorting algorithms like Merge Sort
Now let's move on.
Think of a stack like a stack of books. Books are added to the top and taken from the top. In computer science, we call this LIFO, Last In, First Out.
Here's what that looks like visually:
Initial Stack:
+---+
| D | <- Top
+---+
| C |
+---+
| B |
+---+
| A |
+---+
Bottom
When you add (push) a new book 'E' to the stack:
Stack.push("E"):
+---+
| E | <- Top (Newly added)
+---+
| D |
+---+
| C |
+---+
| B |
+---+
| A |
+---+
Bottom
When you take (pop) a plate off the stack:
Stack.pop("E")
+---+
| D | <- Top (Now at the top after 'E' was removed)
+---+
| C |
+---+
| B |
+---+
| A |
+---+
Bottom
Stacks are again part of the java.util package, similar to LinkedLists. Let's see how we code a Stack:
// Skim, then practice. Make your own examples
// .push() = Stack add
// .pop() = Stack remove
// .empty() = Check if Stack is empty
// .peek() = View top element of Stack
// .search(Object o) = Search element in Stack
// .size() = Get Stack size
import java.util.Stack;
public class StackExample {
public static void main(String[] args) {
Stack<String> stack = new Stack<>();
stack.push("First");
stack.push("Second");
stack.push("Third");
System.out.println("Stack: " + stack);
System.out.println("Top element (peek): " + stack.peek());
System.out.println("Is stack empty? " + stack.empty());
int secondElement = stack.search("Second");
System.out.println("Position of 'Second': " + secondElement);
System.out.println("Stack size: " + stack.size());
System.out.println("Element removed (pop): " + stack.pop());
System.out.println("Stack after pop: " + stack);
}
}Output:
Stack: [First, Second, Third]
Top element (peek): Third
Is stack empty? false
Position of 'Second': 2
Stack size: 3
Element removed (pop): Third
Stack after pop: [First, Second]
While linked lists are adept at handling basic Searching Algorithms like Linear Search and excel in recursive Sorting Algorithms such as Merge Sort, stacks are designed for a different function.
- Linked Lists: Comparable to a two-way street, offering the freedom to access elements at any point.
- Stacks: Similar to a straight path, governed by the Last In, First Out (LIFO) principle, limiting random access unlike linked lists.
- Managing function calls in recursion.
- Parsing expressions in compilers.
- Implementing Depth-First Search (DFS) in graph processing.
Queues operate on the First In, First Out (FIFO) principle. Think of a line of customers waiting to check out at a grocery store. You stand in line from the back and you go as you came. Let's walk through the primary operations of a queue with a simple example:
Imagine a queue starting with three elements: A, B, and C, with A being the first one in line (at the Front) and C the last (at the Back).
Initial Queue:
+---+ +---+ +---+
(<- Front) | A | -> | B | -> | C | (<- Back)
+---+ +---+ +---+
Next, we'll add 'D' to our queue. The enqueue operation adds 'D' to the back of the line, maintaining our order.
Enqueue 'D' (add 'D' - from back):
+---+ +---+ +---+ +---+
(<- Front) | A | -> | B | -> | C | -> | D | (<- Back)
+---+ +---+ +---+ +---+
Now, we'll remove the first element 'A' from the front of the queue. In our case, 'A' will leave the queue, making 'B' the new front element.
Dequeue (remove 'A' - first out) (NOT Deque):
+---+ +---+ +---+
(<- Front) | B | -> | C | -> | D | (<- Back)
+---+ +---+ +---+
This demonstrates the core functionality of a queue, showcasing how it manages elements in a sequential, orderly fashion. Think of customer service, traffic systems, print queues, and restaurant order management.
Keep in mind, we have to import LinkedList and Queue because we use LinkedList as an implementation of the Queue interface to demonstrate Queue functionality.
In simpler terms, this means that while Queue outlines the rules for how a queue should behave, LinkedList provides the actual mechanics and storage to make the queue work. LinkedList is particularly well-suited for this because it allows for efficient insertion and removal of elements at both ends, which is essential for maintaining the FIFO (First In, First Out) principle of queue operations.
So moving onto FIFO:
import java.util.LinkedList;
import java.util.Queue;
// Queue add = .offer()
// Queue remove = .poll()
public class QueueExample {
public static void main(String[] args) {
Queue<String> queue = new LinkedList<>();
// Enqueue: Add elements A, B, C, D
queue.offer("A");
queue.offer("B");
queue.offer("C");
queue.offer("D");
System.out.println("Queue after enqueues: " + queue);
// Dequeue: Removing the front element
String dequeuedElement = queue.poll();
System.out.println("Dequeued element: " + dequeuedElement);
System.out.println("Queue after dequeue: " + queue);
}
}Output:
Queue after enqueues: [A, B, C, D]
Dequeued element: A
Queue after dequeue: [B, C, D]
So, we've covered Arrays, Linked Lists, Stacks, and Queues. Now, it's time to dive into the world of algorithms. Understanding these data structures sets a solid foundation for us to explore how algorithms efficiently manipulate, search, and sort data.
When we talk about searching algorithms, we're diving into the methods of finding specific data within our structures.
Imagine a toolbox – we've got our tools (data structures), and now we need efficient ways to use them.
Searching algorithms are crucial because they dictate how quickly we can access or find data. Learning about arrays, linked lists, and the like was like learning to organize our toolbox; now, we're learning the best ways to use those tools.
If you're new to Java, it's crucial to understand the structure of your code. To jog our memory, let's revisit a snippet from Write Your First Java Program.
// Class Definition
public class HelloWorld {
// Main Method / Driver Code
public static void main(String[] args) {
System.out.println("Hello, World!");
}
}Up to this point, I've been guiding you through adding code just after what's known as the driver code, or the main method. But now, as we step into the world of more complex algorithms, I want to show you how to write your own specialized functions right within the Class Definition.
This way, we separate what the function does (its logic) from the data it works with (inputs and outputs). It's like sorting out our toolbox so that we can easily grab just the right tool—our custom function—whenever we need it.
// Class Definition
public class MyFunction {
// < Write your custom function here >
// Main Method
public static void main(String[] args) {
// < Gather your inputs here >
// < Call your custom function with those inputs and print >
}
}Linear searches are the most basic type of search algorithms, but they're quite straightforward.
Imagine you have an array with five numbers, ranging from 1 to 5, arranged in a random order. Your task is to locate the number 3.
In a linear search, you would:
- Start from the beginning
- Go down the line: If the current element doesn't match the number you're looking for, move to the next element in the array.
- Keep going until you find the target: Once you find an element that matches (in this case, the number 3), print out "Found Target!"
This method ensures that you check each element of the array, making it a reliable, though not necessarily the most efficient, search strategy.
Initial Array:
+---+---+---+---+---+
| 1 | 4 | 3 | 5 | 2 |
+---+---+---+---+---+
Target -> 3
Now let's search for target -> 3:
Check first element:
+---+---+---+---+---+
| 1 | | | | |
+---+---+---+---+---+
Not 3, move to next.
Check second element:
+---+---+---+---+---+
| | 4 | | | |
+---+---+---+---+---+
Not 3, move to next.
Check third element:
+---+---+---+---+---+
| | | 3 | | |
+---+---+---+---+---+
Found 3!
Now that we understood the logic, let's start writing up our code.
public class LinearSearch {
// Linear search method (int arr[] -> input array, int x -> target value)
// Searches each element in order of arr[] to find the target value, x
// If found, returns the index of x. Otherwise returns -1
public int linearSearch(int arr[], int x) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
// Driver code
// Let's look for 1st '10' element
// Ask your linearSearch function to find where your target is within the array
public static void main(String args[]) {
int arr[] = { 2, 3, 4, 10, 40, 10, 5, 10};
int x = 10;
int result = linearSearch(arr, x);
System.out.println("Target found at arr["+result+"]");
}
}Output:
Target found at arr[3]
Given our array int arr[] = { 2, 3, 4, 10, 40 }, it's important to remember that in Java, array indexing starts at 0. So, arr[3] is actually the fourth element in our array, not the third.
I know discussing time complexity might seem a bit dry, but it's crucial for understanding the efficiency of our programs. As we saw in our Big O Notation (MUST KNOW) section, recognizing which algorithms perform better under different conditions is key.
Time Complexity: Linear Search
- Best Case: If the key is at the first index. Complexity: O(1).
- Worst Case: If the key is at the last index, or the search starts from the opposite end. Complexity: O(N), where N is the list size.
- Average Case: O(N).
Now let's move on
If you have 100 million numbers and were told to find a target that was the last element by unforuntae luck, then a linear serach would take way too long.
What if there was a faster method? Assuming our array is sorted, we can cleverly cut down half of the elements in just one move.
- If our target is higher than the midpoint, we'll zoom in on the upper half.
- Conversely, if it's lower, we'll shift our focus to the lower half.
- Rinse and Repeat (but make sure to also check low, mid, and high values)
So how does this look visually?
Initial Array of 10 random numbers:
+---+---+---+---+---+---+---+---+---+---+
| 10| 4 | 3 | 5 | 2 | 9 | 7 | 6 | 8 | 1 |
+---+---+---+---+---+---+---+---+---+---+
Sort the array:
+---+---+---+---+---+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10|
+---+---+---+---+---+---+---+---+---+---+
Now that we have sorted our array, let's look for our target -> 3.
We apply the formula middle = low + (high - low) / 2 to determine the middle index. With 10 elements, our initial low is at index 0 and high is at index 9. Plugging in these values, we get:
middle = 0 + (9 - 0) / 2 = 4.5
Since array indices are integers, we round down to the nearest whole number, resulting in an index of 4 for our middle (which is '5').
We will keep doing this until we find our '3'.
Step 1 (Find the middle):
+---+---+---+---+---+---+---+---+---+---+
| L | | | | M | | | | | H |
+---+---+---+---+---+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10|
+---+---+---+---+---+---+---+---+---+---+
Step 2 (Take the first half and find new middle):
+---+---+---+---+---+---+
| L | | M | | | H |
+---+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 5 | |
+---+---+---+---+---+---+
Middle is 3, which is the target.
Target Found at index 2:
+---+---+---+---+---+---+---+---+---+---+
| | | X | | | | | | | |
+---+---+---+---+---+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10|
+---+---+---+---+---+---+---+---+---+---+
Notice how we didn't update the high value to be the middle value? That's because we've already checked the middle value.
If our target was at this position, we would have found it already! By setting high = middle - 1, we effectively narrow down the search range to the lower half, excluding the middle element which we know is not the target. This smart move cuts down our search time significantly.
Now let's see how this looks in code:
// Initialize low and high pointers
// Continue searching as long as low <= high
// If target equals middle, return its index
// If target is greater, move low to middle + 1
// If target is smaller, move high to middle - 1
// Return -1 if target is not found
public class BinarySearch {
// Binary search method
public int binarySearch(int arr[], int target) {
int low = 0, high = arr.length - 1;
while (low <= high) {
int middle = low + (high - low) / 2;
if (arr[middle] == target)
return middle;
if (arr[middle] < target)
low = middle + 1;
else
high = middle - 1;
}
return -1;
}
// Main method for testing binary search
public static void main(String args[]) {
int arr[] = { 2, 3, 4, 10, 40, 35, 36, 23 };
int target = 10;
// Create an instance of BinarySearch and call binarySearch
BinarySearch instance = new BinarySearch();
int result = instance.binarySearch(arr, target);
System.out.println("Element is present at index: arr["+result+"]");
}
}Output:
Target is present at index: arr[3]
Time Complexity: Binary Search
- Best Case: O(1) – Occurs when the target is at the middle of the array.
- Worst Case: O(log N) – In the worst case, the algorithm will have to split the array until only one element is left.
- Average Case: O(log N) – On average, the algorithm splits the array log N times.
After exploring basic search algorithms like Linear Search and Binary Search, it becomes clear that some search methods requires you to have sorted arrays. This leads us to the world of sorting algorithms, which are as varied and important as searching algorithms.
In the upcoming sections, we'll dive into a few fundamental sorting techniques:
- Bubble Sort
- Selection Sort
- Insertion Sort
Bubble Sort is a straightforward sorting algorithm, introducing you to the world of sorting. It works by repeatedly stepping through the list, comparing adjacent elements and swapping them if they are in the wrong order.
Key Point:
- It's not the most efficient for large datasets. It's more of a beginner's tool to get familiar with how sorting algorithms work.
Breaking it Down:
- Assume
j = 1. if arr[j - 1] > arr[j], then we swap, and continue until the array is sorted.
Let me show you a quick visualization of how a Bubble sort works in action:
Initial Array of 5 numbers:
+---+---+---+---+---+
| 10| 4 | 7 | 2 | 5 |
+---+---+---+---+---+
Now let's bubble sort them.
arr[j - 1] > arr[j]
10 > 4
True, so swap and go to next
Pass 1:
+---+---+---+---+---+
| 4 | 10| 7 | 2 | 5 |
+---+---+---+---+---+
↑ ↑
Swap
+---+---+---+---+---+
| 4 | 7 | 10| 2 | 5 |
+---+---+---+---+---+
↑ ↑
Swap
+---+---+---+---+---+
| 4 | 7 | 2 | 10| 5 |
+---+---+---+---+---+
↑ ↑
Swap
+---+---+---+---+---+
| 4 | 7 | 2 | 5 | 10|
+---+---+---+---+---+
↑ ↑
Swap
Pass 2:
+---+---+---+---+---+
| 4 | 7 | 2 | 5 | 10|
+---+---+---+---+---+
↑ ↑
No Swap
+---+---+---+---+---+
| 4 | 2 | 7 | 5 | 10|
+---+---+---+---+---+
↑ ↑
Swap
+---+---+---+---+---+
| 4 | 2 | 5 | 7 | 10|
+---+---+---+---+---+
↑ ↑
Swap
Pass 3:
+---+---+---+---+---+
| 2 | 4 | 5 | 7 | 10|
+---+---+---+---+---+
↑ ↑
Swap
+---+---+---+---+---+
| 2 | 4 | 5 | 7 | 10|
+---+---+---+---+---+
↑ ↑
No Swap
Pass 4:
+---+---+---+---+---+
| 2 | 4 | 5 | 7 | 10|
+---+---+---+---+---+
↑ ↑
No Swap
The array is now Bubble Sorted.
Now let's see this code in action.
Challenges:
- Learn to swap variables using a 3rd variable called
temp. However, more advnaced methods will require you to just stick with your two variables. - Try to write down your logic first before you code. Don't just dive in hoping things will work out.
The code will start to get more complex so let's divide our code up into 2 parts - Class definition & Driver Code - and let's piece it together at the very end.
Class Definition:
public class BubbleSort {
public void sort(int[] arr) {
int temp;
for (int i = 0; i < arr.length; i++) {
for (int j = 1; j < (arr.length - i); j++) {
if (arr[j - 1] > arr[j]) {
temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
}
}-
The Setup:
- We have a class
BubbleSortwith a methodsortthat takes an arrayarrto sort.
- We have a class
-
Temporary Storage (
temp):- Integer value called
temp.
- Integer value called
-
The Outer Loop (
i):for (int i = 0; i < arr.length; i++)- Think ofias a countdown. It tracks how many elements at the end of the array are sorted.
-
The Inner Loop (
j):for (int j = 1; j < (arr.length - i); j++)- Here,jlooks at each pair of numbers. It stops earlier each time(arr.length - i)because the biggest numbers are already sorted at the end.
-
Making the Swap:
if (arr[j - 1] > arr[j])- If number is bigger than the next one in line, swap them.
To swap:
1. Put `arr[j - 1]` in `temp`.
2. Move `arr[j]` to `arr[j - 1]`.
3. Move `temp` (old `arr[j - 1]`) to `arr[j]`.
* You will learn to swap without the temp variable over time
Now that we have created our Class defintion for BubbleSort, let's see how we can utilize this function in our Driver Code.
This one will be a bit more challenging because we want our output to look a certain way.
Let's write our driver that was similar to our Binary Search.
Driver Code:
public static void main(String[] args) {
int[] arr = {3, 60, 35, 2, 45, 320, 5};
BubbleSort instance = new BubbleSort();
instance.sort(arr);
System.out.print("Bubble Sorted: [");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
if (i < arr.length - 1) {
System.out.print(", ");
}
}
System.out.println("]");
}-
Creating BubbleSort Instance:
BubbleSort instance = new BubbleSort();
This line creates a newBubbleSortobject, like getting a helper for sorting.
-
Printing the Sorted Array with Commas:
for (int i = 0; i < arr.length; i++) { ... }
Starts a loop to go through each element of the sorted array.- Inside the loop:
System.out.print(arr[i]);
Prints the current element.if (i < arr.length - 1) { System.out.print(", "); }
Adds a comma and space after the element if it's not the last one.
-
Closing the Array Presentation:
System.out.println("]");
Closes the presentation with a ']' once all elements are printed.
public class BubbleSort {
public void sort(int[] arr) {
int temp;
for (int i = 0; i < arr.length; i++) {
for (int j = 1; j < (arr.length - i); j++) {
if (arr[j - 1] > arr[j]) {
// Swap elements
temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
}
public static void main(String[] args) {
int[] arr = {3, 60, 35, 2, 45, 320, 5};
BubbleSort instance = new BubbleSort();
instance.sort(arr);
System.out.print("Bubble Sorted: [");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
if (i < arr.length - 1) {
System.out.print(", ");
}
}
System.out.println("]");
}
}Output:
Bubble Sorted: [2, 3, 5, 35, 45, 60, 320]Time Complexity: Bubble Sort
- Best Case: O(n) – Occurs when the array is already sorted. The algorithm only needs to make one pass through the array to confirm it is sorted.
- Worst Case: O(n²) – In the worst case, when the array is sorted in reverse order, the algorithm performs the maximum number of comparisons and swaps.
- Average Case: O(n²) – On average, Bubble Sort compares each element to others in nested loops, leading to quadratic time complexity.
Keep in mind, I've spent a good chunk of time breaking down class definitions and driver codes step by step. Hopefully, you've picked up a lot along the way.
Now, it's your turn to take the wheel a bit. I'll still be unpacking the logic, but reading and understanding the code? Consider it a personal challenge
Selection Sort is a simple and intuitive algorithm that sorts an array by repeatedly finding the minimum element from the unsorted part and putting it at the beginning.
Key Point:
More swap-efficient than Bubble Sort. Ideal when minimizing the number of swaps is crucial.
Why Choose Selection Over Bubble:
Selection Sort minimizes swaps, which can be costly, making it more preferable in scenarios where write operations are significantly more expensive than reads, such as with certain types of memory or large records in databases.
Initial Array of 5 numbers:
+---+---+---+---+---+
| 7 | 1 | 4 | 2 | 3 |
+---+---+---+---+---+
Now let's selection sort them.
Find the minimum number in the array and swap with the first position.
PASS 1 (considering the whole array):
|+++++++++++++++++++|
+---+---+---+---+---+
| 7 | 1 | 4 | 2 | 3 |
+---+---+---+---+---+
↑
Minimum
Swap with first element
+---+---+---+---+---+
| 1 | 7 | 4 | 2 | 3 |
+---+---+---+---+---+
↑ ↑
Swap
PASS 2 (ignoring the first element):
|+++++++++++++++|
+---+---+---+---+---+
| 1 | 7 | 4 | 2 | 3 |
+---+---+---+---+---+
↑
Minimum
Swap with the first element of the unsorted part and repeat...
+---+---+---+---+---+
| 1 | 2 | 4 | 7 | 3 |
+---+---+---+---+---+
↑ ↑
Swap
PASS 3 (ignoring the first two elements):
|+++++++++++|
+---+---+---+---+---+
| 1 | 2 | 4 | 7 | 3 |
+---+---+---+---+---+
↑
Minimum
+---+---+---+---+---+
| 1 | 2 | 3 | 7 | 4 |
+---+---+---+---+---+
↑ ↑
Swap
PASS 4 (ignoring the first three elements):
|+++++++|
+---+---+---+---+---+
| 1 | 2 | 3 | 7 | 4 |
+---+---+---+---+---+
↑
Minimum
+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 7 |
+---+---+---+---+---+
↑ ↑
Swap
RESULT:
+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 7 |
+---+---+---+---+---+
The array is now Selection Sorted.
Initial Array of 5 numbers:
+---+---+---+---+---+
| 5 | 2 | 4 | 3 | 1 |
+---+---+---+---+---+
Now let's insertion sort them.
The array is now Insertion Sorted.
So let's go over the logic in code:
-
The Sorting Loop:
- Pick a
tempvalue:int temp = arr[i]. This is our hero, moving through the array. - Set
j = i - 1. Think ofjas temp's sidekick, always one step behind. - Start from the second element (
i = 1) because the first element alone is already 'sorted'. - Use a
whileloop for the action: As long asjis not at the array's start (j >= 0) andtempis smaller thanarr[j], keep the loop going.
- Pick a
-
Make Room:
- Inside the loop, if
arr[j]is bigger thantemp, shiftarr[j]to the right (arr[j + 1] = arr[j]). This creates space fortemp. - Decrement
juntil you can't swap anymore.j = j - 1can be turned intoj--for short.
- Once
jis less thantemp, or at the start, exit the loop.
- Inside the loop, if
-
Place
temp:- Put
tempin its rightful spot:arr[j + 1] = temp.
- Put
-
Repeat:
- Move to the next element, and repeat the process until the end of the array.
Result: You get a neatly sorted array, with each element finding its perfect place, step by step.
public class InsertionSort {
public void sort(int arr[]) {
for (int i = 1; i < arr.length; i++) {
int temp = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > temp) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = temp;
}
}...And now welcome to our next challenge: Making a second function within your class definition.
Instead of repeatedly tweaking our code in the main method to print arrays in a specific format, why not streamline the process? Let's introduce a dedicated function named PrintArray. This function will handle all our array printing needs, much like we've been doing in our driver code.
- Start with a Bracket:
- Begin the output with
"[", setting the stage for our array elements.
- Begin the output with
- Loop Through Elements:
- Iterate over each element in the already sorted array.
- Comma Management:
- If our element is NOT the last one, we shall add a
","
- If our element is NOT the last one, we shall add a
- Close with a Bracket:
- Once the last element is reached, conclude with
"]".
- Once the last element is reached, conclude with
static void PrintArray(int arr[]) {
System.out.print("[");
for (int i=0; i < arr.length; i++) {
System.out.print(arr[i]);
if (i < arr.length - 1) {
System.out.print(", ");
}
}
System.out.println("]");
}Make sure to end with println and not print if you want to make a new line. You will otherwise see % at the end of your results
public class InsertionSort {
// Sort method
public void sort(int arr[]) {
for (int i = 1; i < arr.length; i++) {
int temp = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > temp) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = temp;
}
}
// Print method
static void PrintArray(int arr[]) {
System.out.print("[");
for (int i=0; i < arr.length; i++) {
System.out.print(arr[i]);
if (i < arr.length - 1) {
System.out.print(", ");
}
}
System.out.println("]");
}
//Driver code
public static void main(String args[]) {
int[] arr = {47, 12, 85, 32, 79, 58, 91, 21, 43, 67, 13, 28, 56, 39, 74};
InsertionSort instance = new InsertionSort();
instance.sort(arr);
PrintArray(arr);
}
}Output:
[12, 13, 21, 28, 32, 39, 43, 47, 56, 58, 67, 74, 79, 85, 91]