myMatrix Source code

createMat

Matrix createMat(int _rows, int _cols);

parameter

int rows : rows of Matrix

int cols : rows of Matrix

Example code

Matrix A = createMat(2, 3);
Matrix A = createMat(5, 5);

printMat

void printMat(Matrix _A, const char* _name)

parameter

_A : printed Matrix

_name : title

Example code

printMat(matA, "matA");
printMat(matB, "matB");

mulScalar

Matrix mulScalar(Matrix _A, double B)

parameter

_A : subject Matrix A

_B : scalar number

Example code

Matrix X = mulScalar(matA, 2);
Matrix X = mulScalar(matB, 5);

mulMat

Matrix mulMat(Matrix _A, Matrix _B);

parameter

A : first Matrix

B : second Matrix

Example code

mulMat(matA, matB);

initMat

void	initMat(Matrix _A, double _val);

parameter

A : subject Matrix

B : initial value

Example code

initMat(matA, 1);

zeros

Matrix	zeros(int _rows, int _cols);

parameter

_rows : rows of Matrix

_cols : columns of Matrix

Example code

Matrix X = zeros(3, 4);

ones

create Matrix of all zeros

Matrix	ones(int _rows, int _cols);

parameter

_rows : rows of Matrix

_cols : columns of Matrix

Example code

Matrix X = ones(3, 3);

transpose

Matrix transpose(Matrix _A);

parameter

A : subject Matrix

Example code

transpose(matA);

copyMat

Matrix	copyMat(Matrix _A);

parameter

A : subject Matrix

Example code

matB = copyMat(matA);

copyVal

void copyVal(Matrix _A, Matrix _B);

parameter

_A : subject Matrix

_B : replicated Matrix

Example code

copyVal(matA, matB);

Practice

These functions are useful tools for making any function in Numerical Programming Class

Numerical Programming API

#include "myNP.h"

Non-Linear Solver

bisection()

select a, b
if f(a)*f(b) appear negative sign, there is a value
it selects (a+b)/2, a | if f((a+b)/2)*f(a)< 0 : b =x;

double bisection(double fn(double _x), double _a, double _b, double _tau)

parameter

fn : function
a : initial value 1
b : initial value 2
tau : error value

example code

double init_1 = -3;
double init_2 = 5;
double tau = 0.00001;

BS_result = bisection(function, init_1, init_2, tau);

NewtonRaphson()

select a
it finds roots as x-intercept of the straight line tangent to the curve at a

double newtonRaphson(double fn(double x), double dfn(double x), double _x0, double _tol)

parameter

fn : function
dfn : differential function
x0 : initial value
tol : tolerance error

example code

float tol = 0.00001;
double NR_result;
double x0 = 1;

NR_result = newtonRaphson(fn, dfn, x0, tol);

Secant()

double secant(double function(double _x), double _x0, double _x1, double _tau)

parameter

function : function
x0 : initial value 1
x1 : initial value 2
tau : error value

example code

float tau = 0.00001;
double SC_result;
double x0 = 1;
double x1 = 3;

SC_result = secant(fn, x0, x1, tau);

NewtonRoots()

Matrix newtonRoots(Matrix X0, Matrix myJacob(Matrix X), Matrix myFunc(Matrix X), float tol)

parameter

X0 : initial value Matrix
myJacob : Jacobian Matrix
myFunc : Function Matrix
tol : tolerance error

example code

Matrix X= zeros(2, 1);
X.at[0][0] = 2.5;
X.at[1][0] = 2;
float tol = 1e-9;

newtonRoots(X, myJacob, myFunc, tol);

Numerical Differentiation

gradient1D()

Differential operation based on data array

void gradient1D(double x[], double y[], double dydx[], int m)

parameter

x[] : x data
y[] : y data
dydx[] : differential coefficient array to return
m : array

example code

int m = 21;
double t[21] = { 0 };
for (int i = 0; i < m; i++) t[i] = 0.2 * i;
double x[] = { -5.87, -4.23, -2.55, -0.89, 0.67, 2.09, 3.31, 4.31, 5.06, 5.55, 5.78, 5.77, 5.52, 5.08, 4.46, 3.72, 2.88, 2.00, 1.10, 0.23, -0.59 };
double  dxdt[21] = { 0 };

gradient1D(t, x, dxdt, m); //m : 데이터 갯수 dxdt : 업데이트할 변수
printVec(dxdt, m);

gradientFunc()

Differential operation based on function

void gradientFunc(double func(const double x), double x[], double dydx[], int m)

parameter

func : function
x[] : x data
dydx[] : differential coefficient array to return
m : array size

example code

double xin = -5.87;
double y = myFunc(xin);
double dydx[21];

gradientFunc(myFunc, t, dydx, m);
printVec(dydx, m);

acceleration()

double Derivative operation based on function

void acceleration(double x[], double y[], double d2ydx2[], int m)

parameter

x[] : x data
y[] : y data
dy2dx2[] : double derivative coefficient array to return
m : array size

example code

int m = 21;
double t[21] = { 0 };
for (int i = 0; i < m; i++) t[i] = 0.2 * i;
double x[] = { -5.87, -4.23, -2.55, -0.89, 0.67, 2.09, 3.31, 4.31, 5.06, 5.55, 5.78, 5.77, 5.52, 5.08, 4.46, 3.72, 2.88, 2.00, 1.10, 0.23, -0.59 };
double  dx2dt2[21] = { 0 };

acceleration(t, x, dx2dt2, m);
printVec(dx2dt2, m);

Integarion

IntegrateRect()

Integration using Rectangular method for discrete data inputs

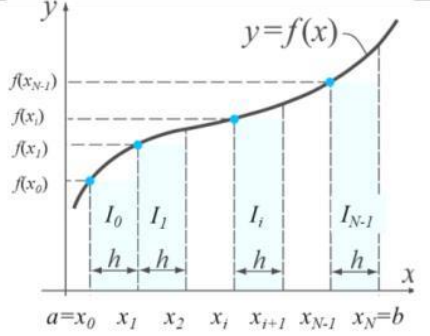
double IntegrateRect(double x[], double y[], int m)

parameter

x[] : x data
y[] : y data
m : array size

example code

double x[] = { 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 };
double y[] = { 0, 3, 8, 20, 33, 42, 40, 48, 60, 12, 8, 4, 3 };
int M = sizeof(x) / sizeof(x[0]);

double I_rect = IntegrateRect(x, y, M);
printf("I_rect = %f\n\n", I_rect);

Trapezode()

Integration using Trapezoidal method for discrete data inputs

double trapz(double x[], double y[], int m)

parameter

x[] : x data
y[] : y data
m : array size

example code

double x[] = { 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 };
double y[] = { 0, 3, 8, 20, 33, 42, 40, 48, 60, 12, 8, 4, 3 };
int M = sizeof(x) / sizeof(x[0]);

double I_trapz = trapz(x, y, M);
printf("I_trapz = %f\n\n", I_trapz);

Simpson13()

Integration using Simpson 1/3 method for discrete data inputs

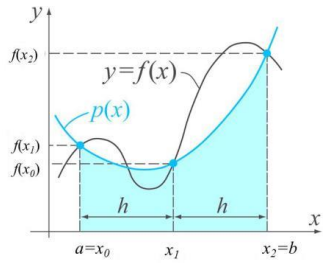
double simpson13(double x[], double y[], int m) {

parameter

x[] : x data
y[] : y data
m : array size

example code

double x[] = { -3, -2.25, -1.5, -0.75, 0, 0.75, 1.5, 2.25, 3 };
double y[] = { 0, 2.1875, 3.75, 4.6875, 5, 4.6875, 3.75, 2.1875, 0 };
int M = sizeof(x) / sizeof(x[0]);

double I_simpson = simpson13(x, y, M);
	printf("I_simpson13  = %f\n\n", I_simpson);

Simpson38()

Integration using Simpson 3/8 method for discrete data inputs

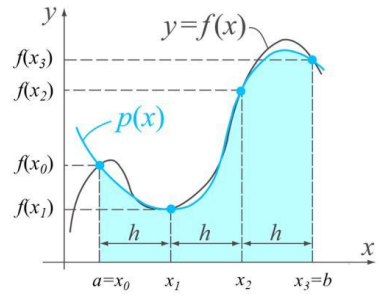
double simpson38(double x[], double y[], int m) {

parameter

x[] : x data
y[] : y data
m : array size

example code

double x[] = { -3, -2.25, -1.5, -0.75, 0, 0.75, 1.5, 2.25, 3 };
double y[] = { 0, 2.1875, 3.75, 4.6875, 5, 4.6875, 3.75, 2.1875, 0 };
int M = sizeof(x) / sizeof(x[0]);

double I_simpson = simpson38(x, y, M);
	printf("I_simpson38  = %f\n\n", I_simpson);

Function integration()

Integration using Simpson 1/3 method for function inputs

double integral(double func(const double _x), double a, double b, int n)

parameter

func : function
a : initial value 1
b : initial value 2
n : array size

example code

int a = -1;
int b = 1;
int n = 12;

double Integrals = integral(myFunc, a, b, n);
printf("func_simpson13  = %f\n\n", Integrals);

Linear Solver

gaussElim()

solves for vector x from Ax=b, a linear system problem Using Gauss Elimination

gaussElim(Matrix A, Matrix vecb, Matrix U, Matrix d, Matrix P)

parameter

A : Matrix A in structure Matrix form. Should be (nxn) square
vecb : vector vecb in structure Matrix form. Should be (nx1)
U : Matrix U in structure Matrix form. Should be (nxn) square
d : vector d in structure Matrix form. Should be (nx1)
P : Partial Pivoting P in structrue Matrix form. Should be (nxn)

example code

Matirx A and vecb data is already filled in notepad

Matrix matA = txt2Mat(path, "prob1_matA");
Matrix vecb = txt2Mat(path, "prob1_vecb");
Matrix matU = copyMat(Q1_matA);
Matrix d = zeros(vecb.rows, 1);
Matrix P = eye(matA.rows, matA.cols);

gaussElim(A, vecb, U, d, P);

LUdecomp()

factors a matrix as the product of a lower triangular matrix and upper triangular matrix

void LUdecomp(Matrix A, Matrix L, Matrix U, Matrix P)

parameter

A : Matrix A in structure Matrix form. Should be (nxn) square
L : Matrix U in structure Matrix form. Should be (nxn) square
U : Matrix U in structure Matrix form. Should be (nxn) square
P : Partial Pivoting P in structrue Matrix form. Should be (nxn)

example code

Matirx A and vecb data is already filled in notepad

Matrix matA = txt2Mat(path, "prob1_matA");
Matrix vecb = txt2Mat(path, "prob1_vecb");
Matrix matU = copyMat(Q1_matA);
Matrix matL = createMat(Q1_matA.rows, Q1_matA.cols);
Matrix P = eye(matA.rows, matA.cols);

LUdecomp(matA, matL, matU, P);

fwdsub()

find y using forward substitution

void fwdsub(Matrix L, Matrix b, Matrix y)

parameter

b : vector b in structure Matrix form. Should be (nx1)
y : vector y in structure Matrix form. Should be (nx1)
L : Matrix L in structure Matrix form. Should be (nxn) square

example code

exsit LUdecomp before

fwdsub(L, vecb, y);

backsub()

find x using back substitution

void backsub(Matrix U, Matrix y, Matrix x)

parameter

x : vector x in structure Matrix form. Should be (nx1)
y : vector y in structure Matrix form. Should be (nx1)
U : Matrix U in structure Matrix form. Should be (nxn) square

example code

exsit LUdecomp before

backsub(matU, y, x);

solveLU()

find x forward substitution, backward substitution

void solveLU(Matrix L, Matrix U, Matrix P, Matrix b, Matrix x)

parameter

L : Matrix U in structure Matrix form. Should be (nxn) square
U : Matrix U in structure Matrix form. Should be (nxn) square
P : Partial Pivoting P in structrue Matrix form. Should be (nxn)
b : vector b in structure Matrix form. Should be (nx1)
x : vector x in structure Matrix form. Should be (nx1)

example code

exsit LUdecomp before

Matrix matL = createMat(matA.rows, matA.cols);
Matrix matU = copyMat(matA);
Matrix P = eye(Q1_matA.rows, Q1_matA.cols);
Matrix vecb = txt2Mat(path, "prob1_vecb");
Matrix x = zeros(vecb.rows, 1);

void solveLU(matL, matU, P, vecb, x);

invMat()

inverse Matrix

double invMat(Matrix A, Matrix Ainv)

parameter

A : Matrix A in structure Matrix form. Should be (nxn) square
Ainv : Matrix Ainv in structure Matrix form. Should be (nxn) square

example code

invMat using LUdecomp, forward substitution, backward substitution

Matrix matA = txt2Mat(path, "prob1_matA");
Matrix matAinv = copyMat(matA);

invMat(matA, matAinv);

Eigenvalue & Eigenvector

QRHousehold()

QR factorization

void QRHousehold(Matrix A, Matrix Q, Matrix R)

parameter

A : Matrix A in structure Matrix form. Should be (nxn) square
Q : Matrix Q in structure Matrix form. Should be (nxn) square
R : Matrix R in structure Matrix form. Should be (nxn) square

example code

Matrix matA = txt2Mat(path, "prob_matA");
Matrix matQ = copyMat(matA);
Matrix matR = copyMat(matA);

QRHousehold(matA, matQ, matR);

eig()

eigenvalue

Matrix eig(Matrix A)

parameter

A : Matrix A in structure Matrix form. Should be (nxn) square

example code

apply QRHousehold internal

Matrix matA = txt2Mat(path, "prob_matA");

eigenvalue = eig(matA);

eigvec()

eigenvector

Matrix eigvec(Matrix A)

parameter

A : Matrix A in structure Matrix form. Should be (nxn) square

example code

apply invMat internal

Matrix matA = txt2Mat(path, "prob_matA");

eigenvector = eigvec(matA);

ODE-IVP

odeEU()

solve ordinary differential equation using Euler explicit method ordinary

void odeEU(double myfunc(const double t, const double y), double y[], double t0, double tf, double h, double y0)

odeEM()

solve ordinary differential equation using Euler Modified method ordinary

void odeEM(double myfunc(const double t, const double y), double y[], double t0, double tf, double h, double y0)

odeRK2()

solve ordinary differential equation using Runge-Kutta second method ordinary

void odeRK2(double myfunc(const double t, const double y), double y[], double t0, double tf, double h, double y0)

odeRK3()

solve ordinary differential equation using Runge-Kutta third method ordinary

void odeRK3(double myfunc(const double t, const double y), double y[], double t0, double tf, double h, double y0)

parameter

myfunc : function with t, y
y[] : allocated array y
t0 : initial time value
tf : final time value
h : interval value
y0 : initial y value

example code

double  t0 = 0; double tf = 0.1;
double h = 0.001;
double N = (tf - t0) / h + 1;
double t = 0;
double* y = (double*)malloc(sizeof(double) * N);
double y0 = 0;

/*double myfunc(const double t, const double y)
{
	int i = 0;
	double tau = 1;
	double T = 1 / tau;
	double f = 10;
	double Vm = 1;
	double w = 2 * PI * f * t;
	double funcx = -T * y + 1 * Vm * cos(w);
	return funcx;
}*/

odeEU(myfunc, y, t0, tf, h, y0);
odeEM(myfunc, y, t0, tf, h, y0);
odeRK2(myfunc, y, t0, tf, h, y0);
odeRK3(myfunc, y, t0, tf, h, y0);

sys2RK2()

solve secondary differential equation using Runge-Kutta second method ordinary

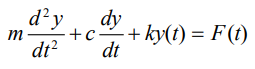
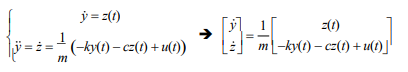
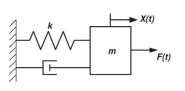
void sys2RK2(void mckfunc(const double t, const double Y[], double dYdt[]), double y1[], double y2[], double t0, double tf, double h, double y1_init, double y2_init)

parameter

mckfunc : function with t, y, dydt
y1[] : y, ex) y[0] = y, y[1] = dy/dt
y2[] : z, ex) z[0] = dy/dt, z[1] = d2y/dt2
t0 : initial time value
tf : final time value
h : interval value
y1 : initial y value
y2 : initial dy/dt value

example code

double t0 = 0; double tf = 1;
double h = 0.01;
double N = (tf - t0) / h + 1;
double t = 0;
double* y1 = (double*)malloc(sizeof(double) * N); //y함수
double* y2 = (double*)malloc(sizeof(double) * N); //z함수
double y1_init = 0;
double y2_init = 0.2;

/*
void mckfunc(const double t, const double Y[], double dYdt[])
{
	double m = 1; double c = 7; double k = 6.9; double f = 5;
	double Fin = 2 * cos(2 * PI * f * t); 
	dYdt[0] = Y[1]; //1번째 풀어야 할 미방식


	// EXERCISE: MODIFY HERE
	dYdt[1] = -Y[1] * c / m - Y[0] * k / m + Fin / m; //z값
}
*/

sys2RK2(mckfunc, y1, y2, t0, tf, h, y1_init, y2_init);

Linear Regression

linearRegression()

straight line that fits the data

Matrix	linearRegression(Matrix _x, Matrix _y)

parameter

x : x data array Matrix. should be (nx1)
y : y data array Matrix. should be (nx1)

example code

int M = 6; //number of data
double T_array[] = { 30, 40, 50, 60, 70, 80 };
double P_array[] = { 1.05, 1.07, 1.09, 1.14, 1.17, 1.21 };
Matrix T = arr2Mat(T_array, M, 1);
Matrix P = arr2Mat(P_array, M, 1);

Matrix z = linearRegression(T, P);
double answer = z.at[0][0] * 100 + z.at[1][0]; //particular y-point at x-point

printMat(T, "T");
printMat(P, "P");
printMat(z, "z");
printf("answer = %lf \n", answer);

polyfit()

curve that fits the data

void polyfit(Matrix _x, Matrix _y, Matrix _z, int n)

parameter

x : x data array Matrix. should be (nx1)
y : y data array Matrix. should be (nx1)
z : coefficient Matrix. should be ((n+1)x1)
n : curve function order

example code

int n = 4; // curve function order
double strain[] = { 0, 0.4, 0.8, 1.2, 1.6, 2.0, 2.4, 2.8, 3.2, 3.6, 4.0, 4.4, 4.8, 5.2, 5.6, 6.0 };
double stress[] = {0, 3, 4.5, 5.8, 5.9, 5.8, 6.2, 7.4, 9.6, 15.6, 20.7, 26.7, 31.1, 35.6, 39.3, 41.5};

Matrix Strain = arr2Mat(strain, N, 1);
Matrix Stress = arr2Mat(stress, N, 1);
Matrix a = zeros(n+1, 1); //function coefficient

polyfit(Strain, Stress, a, n);
printMat(a, "a");

Name		Name	Last commit message	Last commit date
Latest commit History 10 Commits
ODE Programming		ODE Programming
.gitattributes		.gitattributes
.gitignore		.gitignore
ODE Programming.sln		ODE Programming.sln
README.md		README.md
SECURITY.md		SECURITY.md

dlsrkss/ODE-Programming

Folders and files

Latest commit

History

Repository files navigation

myMatrix Source code

createMat

printMat

mulScalar

mulMat

initMat

zeros

ones

transpose

copyMat

copyVal

Practice

Numerical Programming API

Non-Linear Solver

bisection()

parameter

example code

NewtonRaphson()

parameter

example code

Secant()

parameter

example code

NewtonRoots()

parameter

example code

Numerical Differentiation

gradient1D()

parameter

example code

gradientFunc()

parameter

example code

acceleration()

parameter

example code

Integarion

IntegrateRect()

parameter

example code

Trapezode()

parameter

example code

Simpson13()

parameter

example code

Simpson38()

parameter

example code

Function integration()

parameter

example code

Linear Solver

gaussElim()

parameter

example code

LUdecomp()

parameter

example code

fwdsub()

parameter

example code

backsub()

parameter

example code

solveLU()

parameter

example code

invMat()

parameter

example code

Eigenvalue & Eigenvector

QRHousehold()

parameter

example code

Packages