Clash Royale Season 35 Analysis

This is a data analysis for my Clash Royale Season 35 battles, as a log bait player (except for one X-Bow battle by mistake). The goals of the current analysis are:

Part I: Exploratory Data Analysis:

• Explore patterns of win/defeat and investigate my own win rate of the current season.
• Investigate the trophy change distribution (+ve/-ve) after each battle.
• Explore patterns of win/defeat streaks.
• Finding out the most common cards in my opponents decks.

Part II: Inference:

• Build a Bayesian model to infer distributions for: win rate, positive trophy change and negative trophy change.
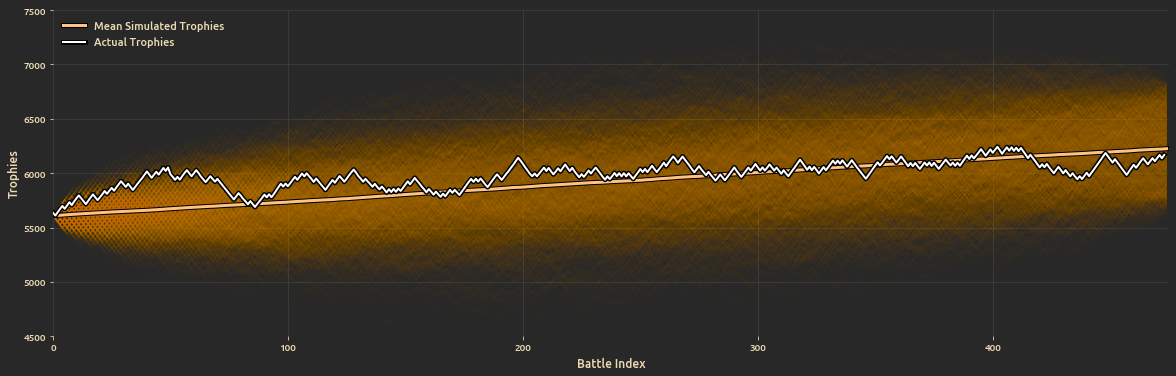
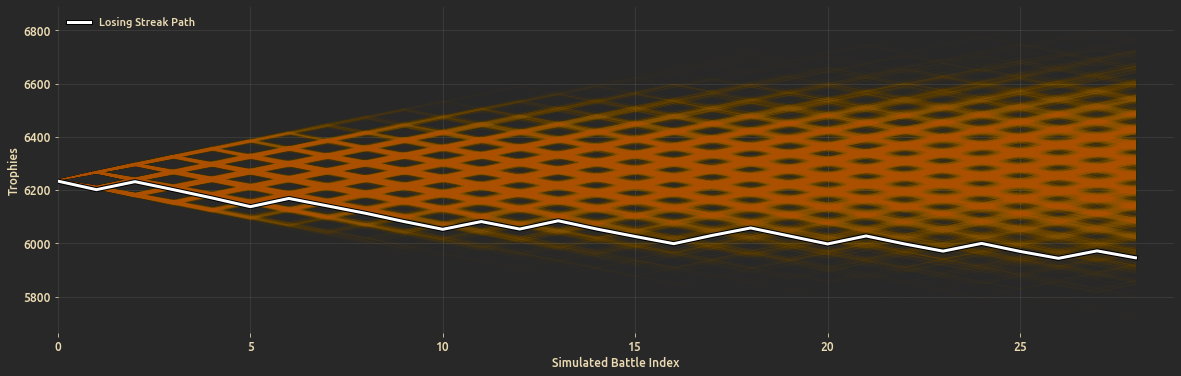
• Simulate random walk battles to compare actual progression vs. the simulated battles.
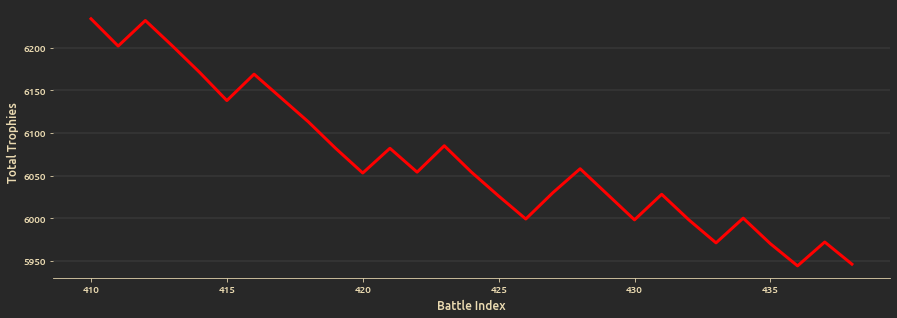
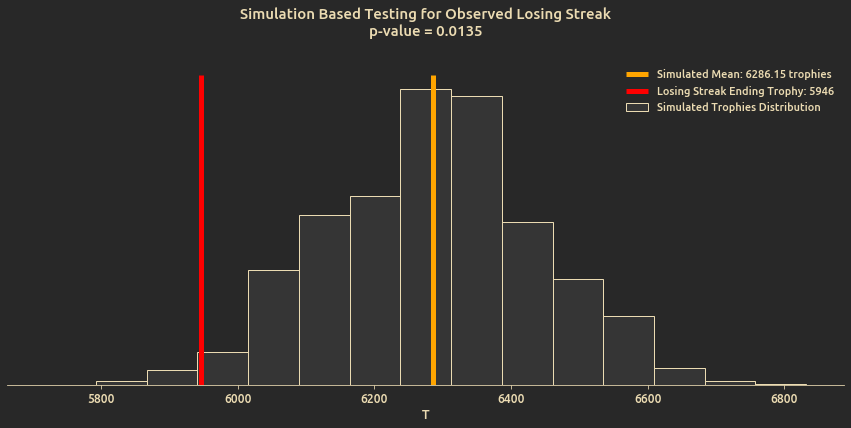
• Test a particular observed lose streak and calculate the probability of its occurence by simulating a random battle walks.
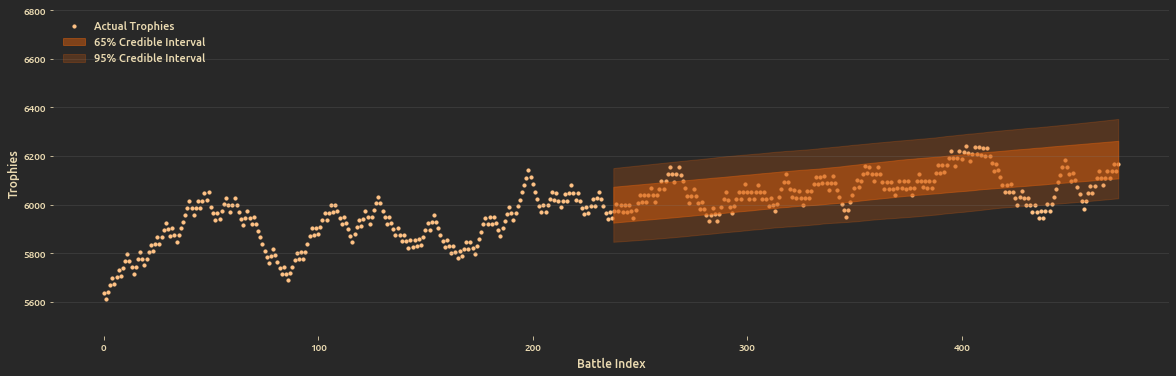
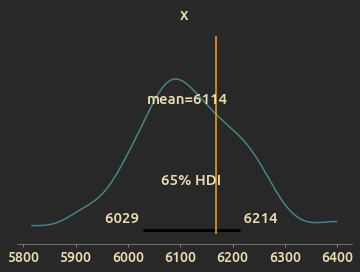
• Build a Bayesian linear regression model to predict the season ending trophies.

Part I: Exploratory Data Analysis

Data have been collected on a daily basis using miner.py, and in data.csv we have 474 battles, with the following summary statistics:

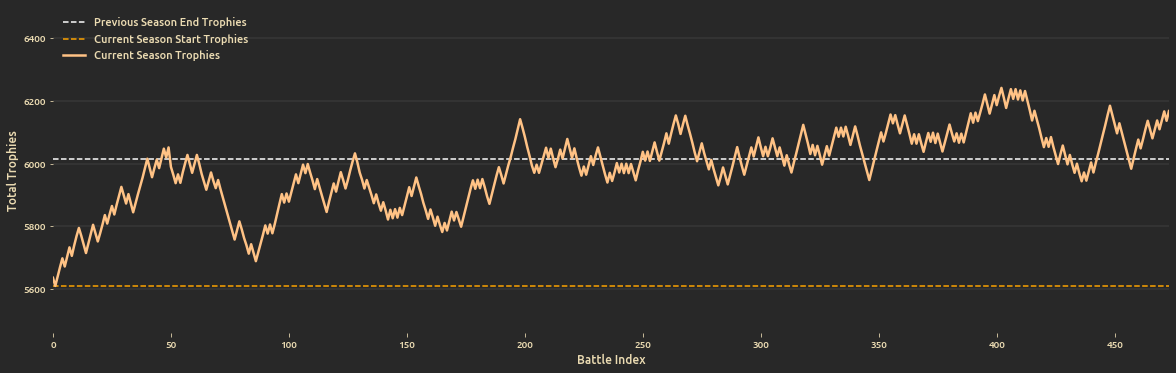
Season Starting Trophies = 5609 trophies
Season Ending Trophies = 6168 trophies
Overall Observed Win rate = 51.27%
Total Trophy Change since season start = 650 trophies
Total number of battles = 474 battles
Active playing days = 32 days
Avg. rate of trophy increase = 20.31 trophies/day

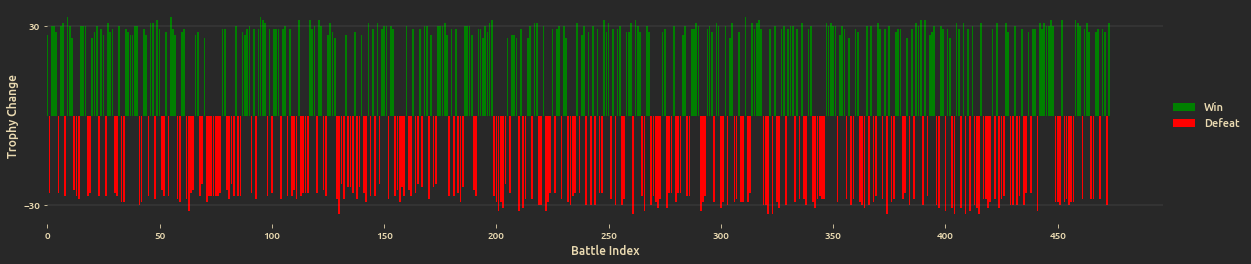
Let's visualize battles outcome (win/defeat), coupled with trophy gain/loss:

And progression of trophies since season start until the final battle:

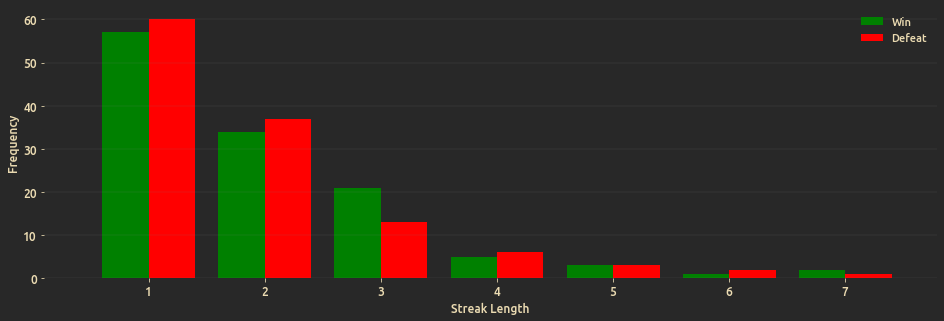
How often did win/defeat streaks occur?

What are our opponents most common cards?

Note: this does not sum to 100% because one opponent can have a mix of most common card in their deck, the following plot shows the percentage of having a specific card in all decks I have faced.

Part II - Bayesian Inference and Simulation

Win Rate Distribution

We don't treat the win rate as just the observed fixed value, but as a random variable. We assume that our data $\mathcal{D} = \{ 1, 0, 1, 1, 0 ,\dots \}$ (each battle outcome) is independent and identically distributed ( $\text{i.i.d.}$ ) (I believe that this is not a valid assumption, but we will test how plausible this assumption is), we also assume a prior uniform distribution of the win rate, and we try to infer the win rate posterior distribution under the assumption of a Bernoulli likelihood.

Prior:

$$ p(\alpha) = \text{Uniform}(0,1) $$

Likelihood:

$$ p(\mathcal{D} \mid \alpha) = \prod p(\text{win} = 1 \mid \alpha) = \text{Bernoulli}(\alpha)$$

Posterior:

$$ p(\alpha \mid \mathcal{D}) \propto p(\mathcal{D} \mid \alpha) \ p(\alpha)$$

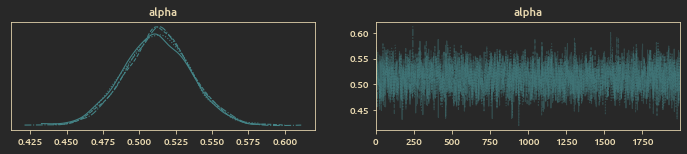
Win rate trace plot:

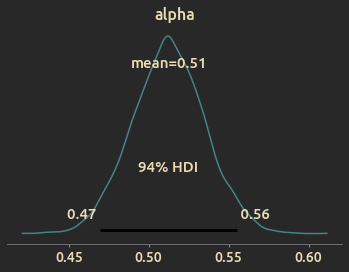
Posterior distribution of win rate $\alpha$:

Trophy Change Distribution

How much trophies do we expect to win/lose after each battle? to answer this we model the observed trophy change (27, 29, 29, 30, .., 33) as a Categorical distribution with a Drichlet prior, for both the positive and negative change.

Prior: $$p_+ \sim \text{Dirichlet}([1, \dots, 1])$$ $$p_- \sim \text{Dirichlet}([1, \dots, 1])$$

Likelihood: $$T_+ \sim \text{Categorical} (p_+)$$ $$T_- \sim \text{Categorical} (p_-)$$

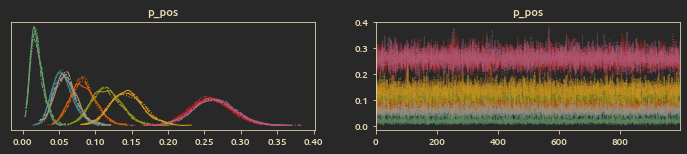
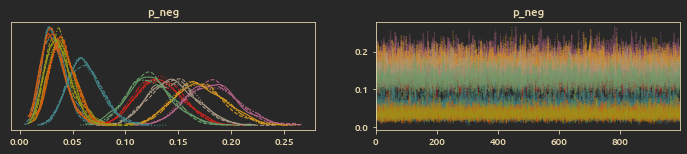
Trace plots for $p_+$ and $p_-$:

Distribution plot of positive and negative trophy change (at posterior mean values):

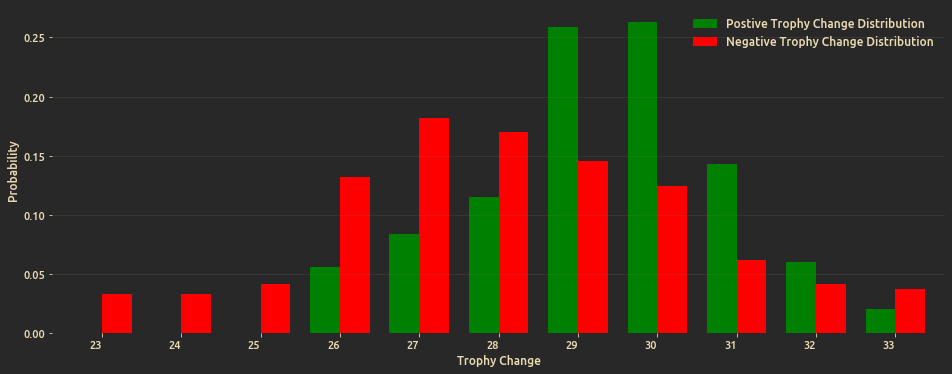
One can conclude that for me the game was on average more rewarding than it was punishing. I was able to win more trophies than I lost, mode of positive trophy change is 30 while for negative trophy change it's 27, so despite the low win rate, the game on average is rewarding.

How valid is the assumption that battle outcomes are independent?

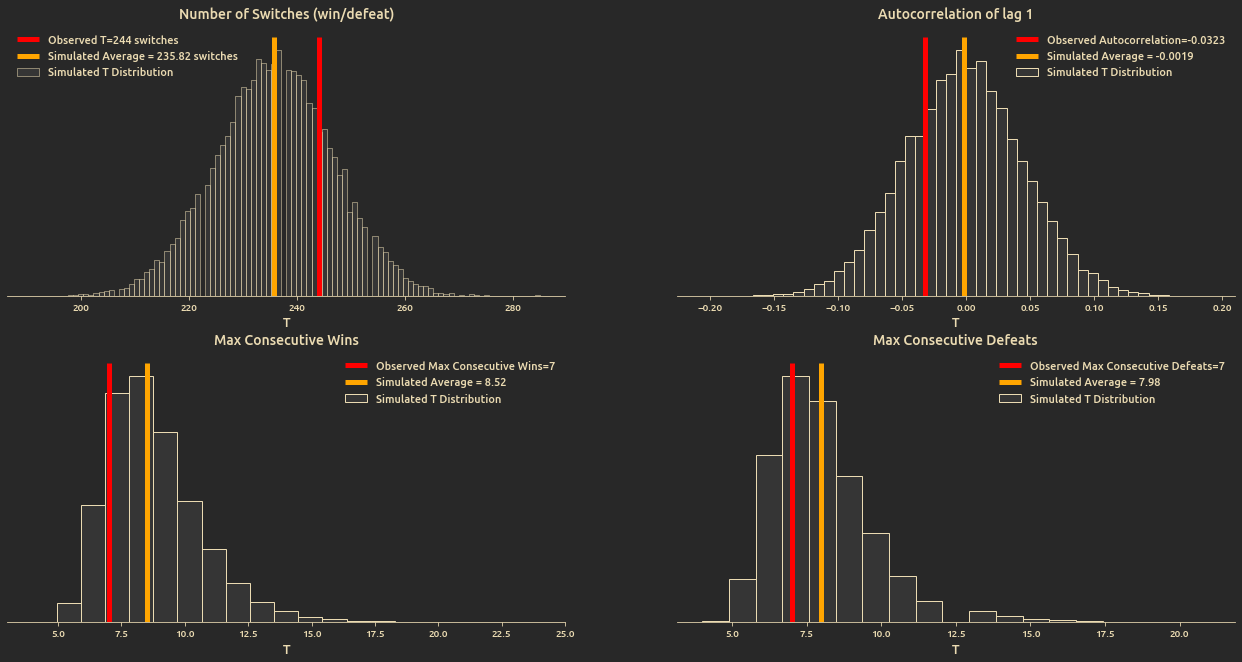
I don't think each battle outcome is independent, but if we proceeded anyway to assume that, and given the data we have, is this a valid assumption? In order to test this we define a 4 Test statistics:

1. The number of switches between wins and defeats.
2. Autocorrelation of lag 1
3. Maximum consecutive wins (consecutive ones)
4. Maximum consecutive defeats (consecutive zeroes)

We draw large enough samples from posterior predictive distribution and find the distribution of each test statistic $T$ and compare against the observed value of $T$.

Yet, we found no significant difference from the mean:

Simulate random walk battles, since season start

TODO: Add model formulation, results and summary

Predict season ending trophy, based on half season battles

TODO: Add model formulation, results and summary

Linear regression model parameters trace plot:

Testing the probability of a particular observed losing streak

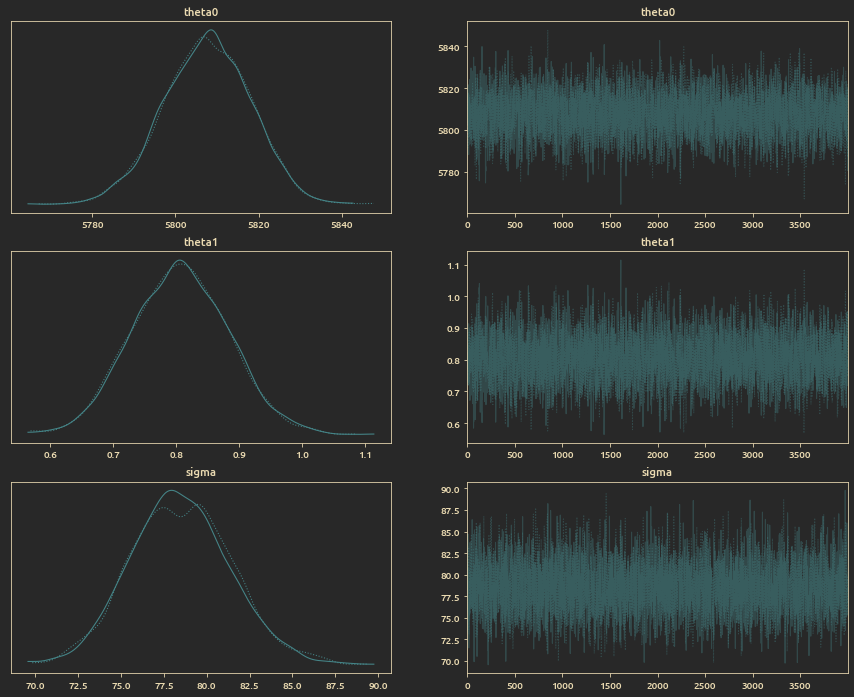
TODO: Explain the need for this and add model forumlation, results and summary.