-
-
Notifications
You must be signed in to change notification settings - Fork 740
Description
There are some trees, where each tree is represented by (x,y) coordinate in a two-dimensional garden. Your job is to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Your task is to help find the coordinates of trees which are exactly located on the fence perimeter.
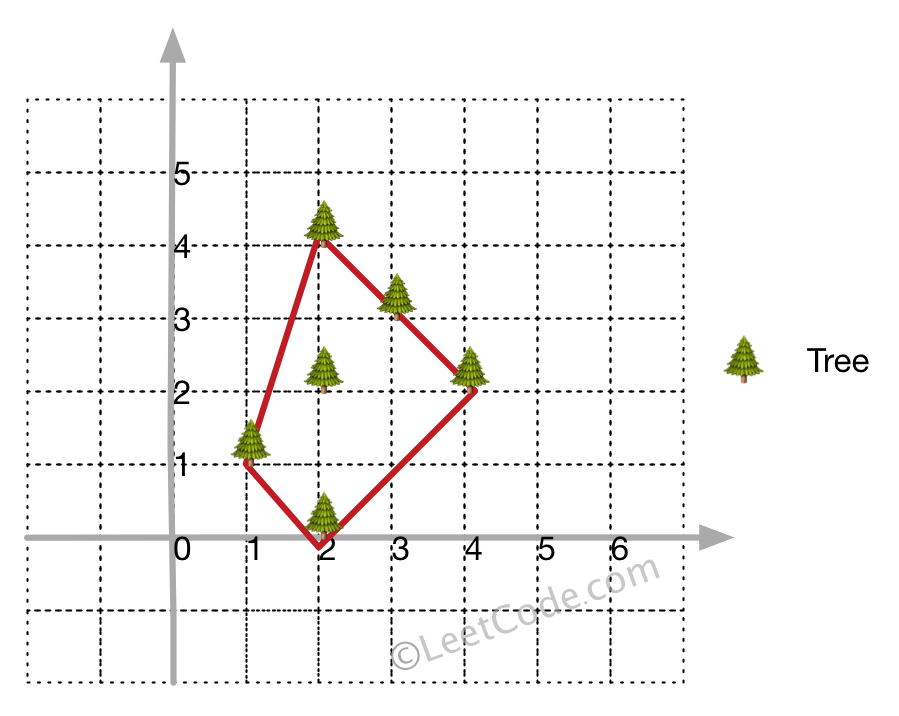
Example 1:
**Input:** [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
**Output:** [[1,1],[2,0],[4,2],[3,3],[2,4]]
**Explanation:**
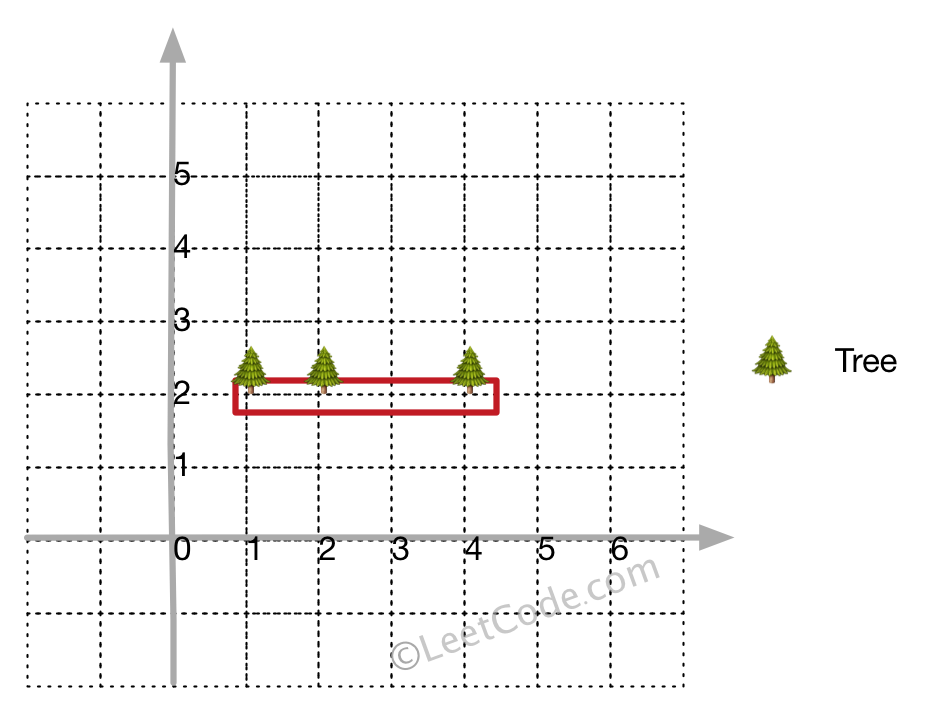
Example 2:
**Input:** [[1,2],[2,2],[4,2]]
**Output:** [[1,2],[2,2],[4,2]]
**Explanation:**
Even you only have trees in a line, you need to use rope to enclose them.
Note:
- All trees should be enclosed together. You cannot cut the rope to enclose trees that will separate them in more than one group.
- All input integers will range from 0 to 100.
- The garden has at least one tree.
- All coordinates are distinct.
- Input points have NO order. No order required for output.
这道题给了我们一些树,每个树都有其特定的坐标,让我们用最少的栅栏将其全部包住,让我们找出在栅栏边上的树。其实这道题是凸包问题,就是平面上给了一堆点,让我们找出一个多边形,正好包括了所有的点。凸包问题的算法有很多,常见的有八种,参见wiki上的这个帖子。我们来看一种比较常见的算法,卷包裹Gift wrapping算法,又叫Jarvis march算法。这种算法的核心像一种卷包裹的操作,比如说我们把每个点当成墙上的钉子,然后我们有一个皮筋,我们直接将皮筋撑的老大,然后套在所有钉子上松手,其自动形成的形状就是要求的凸包,也是凸多边形。脑海中有没有产生这个画面?撑起皮筋的边缘点就是我们要求的关键的结点,形象的图文讲解可以参见这个帖子。
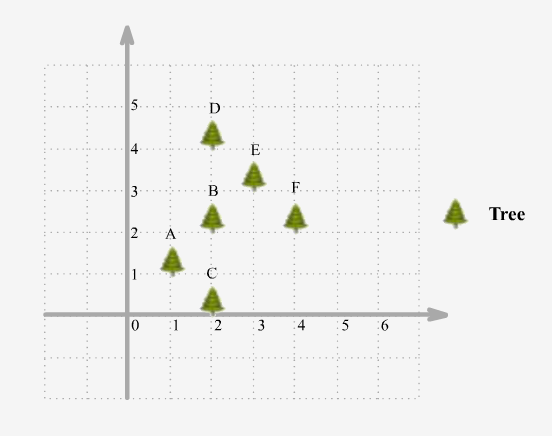
我们的目标是找到这些点,做法是先找到一个边缘点,然后按一个方向转一圈,找到所有的边缘点,当再次找到起始的边缘点时结束循环。起始点的选择方法是找横坐标最小的点,即最左边的点,如果有多个横坐标相同且最小的点也没有关系,其中任意一个都可以当作起始点。因为某个点的横坐标或纵坐标任意一个是最小或最大时,该点一定是边缘上的点。我们把这个起始点标记为first,其坐标标记为firstIdx,然后我们建立一个当前点遍历cur,初始化为first,当前点坐标curIdx,初始化为firstIdx。然后我们进行循环,我们目标是找到下一个边缘点next,初始化其为数组中的第一个点,在例子1中,起始点也是数组中的第一个点,这样cur和next重合了,不过没有关系,这是个初始化而已。好,现在两个点已经确定了,我们还需要一个点,这样三个点就可以利用叉积来求出向量间的夹角,从而根据正负来判断是否为边缘点。第三个点的选择就从数组中的第二个点开始遍历,如果遍历到了cur点,直接跳过。然后此时我们算三个点之间的叉积Cross Product,不太了解叉积的菊苣们可以google一些帖子看一看,简单的来说,就是比如有三个点A,B和C,那么叉积就是求和向量BA,BC都垂直的一个向量,等于两个向量的长度乘以夹角的正弦值。在之前那道Convex Polygon中,我们就是根据叉积来判断是否是凸多边形,要保持凸多边形,那么每三个点的叉积要同正或同负。这有什么用呢,别急,一会再说。先来说之前的cur和next重合了的情况,根据叉积的计算方法,只要有两个点重合,那么叉积就为0。比如当cur和next都是A,points[i]是B时,cross是0,此时我们判断如果points[i]到cur的距离大于next到cur的距离的话,将next移动到points[i]。为啥要判断距离呢,我们假设现在有种情况,cur是D,next是E,points[i]是F,此时的cross算出是0,而且FD的距离大于ED的距离,则将next移动到F点,是正确的。但假如此cur是D,next是F,pionts[i]是E,此时cross算出来也是0,但是ED的距离小于FD的距离,所以不用讲next移动到E,这也make sense。
好,还有两种情况也需要移动next,一种是当next点和cur点相同的时候直接移动next到points[i],其实这种情况已经在上面的分析中cover了,所以这个判断有没有都一样,有的话能省几步距离的计算吧。还有一种情况是cross大于0的时候,要找凸多边形,cross必须同正负,如果我们设定cross大于0移动next,那么就是逆时针来找边缘点。当我们算出来了next后,如果不存在三点共线的情况,我们可以直接将next存入结果res中,但是有共线点的话,我们只能遍历所有的点,再次计算cross,如果为0的话,说明共线,则加入结果res中。在大神的帖子中用的是Set可以自动取出重复,C++版本的应该使用指针的Point,这样才能让set的插入函数work,不加指针的话就不能用set了,那只能手动去重复了,写个去重复的子函数来filter一下吧,参见代码如下:
class Solution {
public:
vector<Point> outerTrees(vector<Point>& points) {
vector<Point> res;
Point first = points[0];
int firstIdx = 0, n = points.size();
for (int i = 1; i < n; ++i) {
if (points[i].x < first.x) {
first = points[i];
firstIdx = i;
}
}
res.push_back(first);
Point cur = first;
int curIdx = firstIdx;
while (true) {
Point next = points[0];
int nextIdx = 0;
for (int i = 1; i < n; ++i) {
if (i == curIdx) continue;
int cross = crossProduct(cur, points[i], next);
if (nextIdx == curIdx || cross > 0 || (cross == 0 && dist(points[i], cur) > dist(next, cur))) {
next = points[i];
nextIdx = i;
}
}
for (int i = 0; i < n; ++i) {
if (i == curIdx) continue;
int cross = crossProduct(cur, points[i], next);
if (cross == 0) {
if (check(res, points[i])) res.push_back(points[i]);
}
}
cur = next;
curIdx = nextIdx;
if (curIdx == firstIdx) break;
}
return res;
}
int crossProduct(Point A, Point B, Point C) {
int BAx = A.x - B.x;
int BAy = A.y - B.y;
int BCx = C.x - B.x;
int BCy = C.y - B.y;
return BAx * BCy - BAy * BCx;
}
int dist(Point A, Point B) {
return (A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y);
}
bool check(vector<Point>& res, Point p) {
for (Point r : res) {
if (r.x == p.x && r.y == p.y) return false;
}
return true;
}
};
类似题目:
参考资料:
https://en.wikipedia.org/wiki/Convex_hull_algorithms
http://www.cnblogs.com/Booble/archive/2011/02/28/1967179.html
https://discuss.leetcode.com/topic/89340/quickhull-c-solution-29ms
https://discuss.leetcode.com/topic/89745/c-and-python-easy-wiki-solution