Newton - Modeling and simulation of planetary motion in C

This code was written in the mid 90s, for pure fun and as just an exercise.

The main idea is, having a set of N bodies of a given mass, to integrate the gravitational forces exerted over each body into velocity and then into position, following an Euler scheme. For further details please check the full article I wrote in my github.io page regarding this problem.

Running the example

Just compile the code and run it

$ make
$ ./newton

For Debian users, you can install the SDL dependencies as:

sudo apt-get install libsdl1.2-dev

Code Details

The code is platform-dependent, as it uses some basic graphic routines. It was originally written for MS-DOS, using the protected mode and the Mode 13h, compiling with the DJGPP programming platform under RHIDE. As this platform is from the past, you can either run it under an emulator like DOSBox, or compile it using the SDL 1.2 wrapper you'll find in the code.

This SDL wrapper, only tested under GNU/Linux, is the only platform-dependent code, and is implemented in files mode13h.h and mode13h.c. In order to switch between a native MS-DOS platform and SDL you must use the DOS symbol (when present, it assumes a native MS-DOS platform, otherwise it will use SDL).

The main algorithm is coded in file newton.c, and it just computes the force exerted over each body, and then velocity and position.

A body is modelled with the struct body_t, which considers the position and velocity. Before starting the integration algorithm, you must create the bodies with the createBody() function, providing initial position, initial velocity and mass.

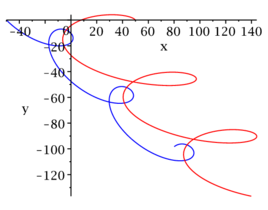
Also, you can specify whether or not the body is fixed at its position, to simulate fictitious situations, suitable to being validated against Keppler's laws (you can visually check how the two first laws hold when only two bodies interact). Another way to do this with real cases is by using the bodyref variable: when this variable is not null, the camera will follow the selected body.

Other useful parameters are scale_factor, to fit the required space in the screen, and calculations_per_plot, that allows you to enable frame dropping, computing with enough accuracy without having to plot all the solutions.

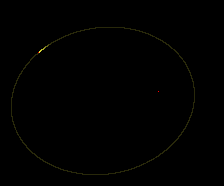
The source code includes an example of an Earth-Moon system, where you can check that, given realistic data for the initial values and masses, some other parameters like the orbital period match the empirical values.

Resources

• Algorithm explanation in my github.io page
• Example video running under DOSBox.