Graph Algorithms for Technical Interviews - Full Course

⭐️ Course Contents ⭐️

Youtube Video 📺

⌨️ (0:00:00) course introduction

⌨️ (0:02:23) graph basics

⌨️ (0:07:10) depth first and breadth first traversal

⌨️ (0:29:13) has path

⌨️ (0:42:11) undirected path

⌨️ (1:00:44) connected components count

⌨️ (1:13:29) largest component

⌨️ (1:24:03) shortest path

⌨️ (1:39:36) island count

⌨️ (1:58:52) minimum island

⌨️ (2:12:05) outro

Graphs Introduction

• Graphs = Nodes+Edges

• Type of Graphs

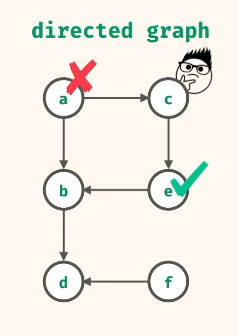
In directed graphs, we have to obey the directions of the arrowheads, ie., If we move from A to C, we can only head to E and not back to A.

• Terminologies

Any node accessible through an edge is called Neighbour node.

• Representing a Graph Data Structure

We would use a hashmap/dictionary to represent graphs as an adjacency list

In this key-value pair, we have the neighbours associated with each node as a key.

Graph Based Algorithms

1. Doing Traversal - Depth First and Breadth First

• Depth First Traversal

We start from a node A and move deep through the nodes till we read deadend. ie., A -> B -> D

Now we move to C. ie., A -> C -> E -> B -> D

We can see some double traversal as well.

• Breadth First Traversal

We start from Node A and move to B, then A move to C

NOTE: DFT is unidirectional and runs till endpoint is reached before switching directions. BFT is uniform traversal and it runs evenly spread out from the starting node.

❓ Implementing in code

DFT - Steps [STACK]

1. We start with A and check its neighbours - C, B; We push C and then B to the stack; Print A
2. Now we pop the stack, we use B as the Current node and check its neighbours - D; Push D to the Stack ; Print B
3. Now we pop stack, we use D as the Current node and check its neighbours - F; Push F to the stack; Print D
4. Pop the stack, F has no neighbours; Print F
5. We have C in the stack, we use C and get its neighbours - E; Push E to stack; Print C
6. Pop the stack finally, we have just E left; Print E.

BFT - Steps [QUEUE]

1. Start with A, Push A to Queue; pop the Queue, A is the Current node; Print A
2. Push B and then C to the Queue, if we want to travel to B first then C; Queue has B and then C in it; pop the queue; B is the Current node; Check the neighbours of B - we have D; Print B
3. In the queue - C and then D; Pop the queue; C is the Current node; C has the neighbours - E; Push it to back of Queue; Print C
4. In the queue - D and then E; Pop the queue; D is the Current node; D has neighbours - F; Push it to back if the Queue; Print D
5. In the queue - E and then F; Pop the queue; E is the Current node; E and F both have no neighbours so we print E and then F

Problem 1 - Has Path

Write a function, hasPath, that takes in an object representing the adjacency list of a directed acyclic graph and two nodes (src, dst). The function should return a boolean indicating whether or not there exists a directed path between the source and destination nodes.

NOTE:

Cyclic vs Acyclic graph - If I start with a node and end up back in it, its cyclic else its not.

Test cases -

# Test case 1

const graph = {
  f: ['g', 'i'],
  g: ['h'],
  h: [],
  i: ['g', 'k'],
  j: ['i'],
  k: []
};

hasPath(graph, 'f', 'k'); // true

# Test Case 2

const graph = {
  f: ['g', 'i'],
  g: ['h'],
  h: [],
  i: ['g', 'k'],
  j: ['i'],
  k: []
};

hasPath(graph, 'f', 'j'); // false

Test Case 1 Image:

Problem 2 - Undirected Path

Write a function, undirectedPath, that takes in an array of edges for an undirected graph and two nodes (nodeA, nodeB). The function should return a boolean indicating whether or not there exists a path between nodeA and nodeB.

Test Cases

# test case 1

const edges = [
  ['i', 'j'],
  ['k', 'i'],
  ['m', 'k'],
  ['k', 'l'],
  ['o', 'n']
];

undirectedPath(edges, 'j', 'm'); // -> true

# test case 2

const edges = [
  ['i', 'j'],
  ['k', 'i'],
  ['m', 'k'],
  ['k', 'l'],
  ['o', 'n']
];

undirectedPath(edges, 'k', 'o'); // -> false