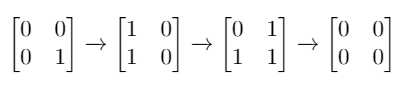Weekly Contest 166

[lihe]

5279. Subtract the Product and Sum of Digits of an Integer

Easy

Given an integer number n, return the difference between the product of its digits and the sum of its digits.

Example 1:

Input: n = 234
Output: 15 
Explanation: 
Product of digits = 2 * 3 * 4 = 24 
Sum of digits = 2 + 3 + 4 = 9 
Result = 24 - 9 = 15

Example 2:

Input: n = 4421
Output: 21
Explanation: 
Product of digits = 4 * 4 * 2 * 1 = 32 
Sum of digits = 4 + 4 + 2 + 1 = 11 
Result = 32 - 11 = 21

Constraints:

• 1 <= n <= 10^5

class Solution {
    public int subtractProductAndSum(int n) {
        int sum = 0, mum = 1;
        while(n != 0){
            sum += n % 10;
            mum *= n % 10;

            n /= 10;
        }
        return mum - sum;
    }
}

5280. Group the People Given the Group Size They Belong To

Medium

There are n people whose IDs go from 0 to n - 1 and each person belongs exactly to one group. Given the array groupSizes of length n telling the group size each person belongs to, return the groups there are and the people's IDs each group includes.

You can return any solution in any order and the same applies for IDs. Also, it is guaranteed that there exists at least one solution.

Example 1:

Input: groupSizes = [3,3,3,3,3,1,3]
Output: [[5],[0,1,2],[3,4,6]]
Explanation: 
Other possible solutions are [[2,1,6],[5],[0,4,3]] and [[5],[0,6,2],[4,3,1]].

Example 2:

Input: groupSizes = [2,1,3,3,3,2]
Output: [[1],[0,5],[2,3,4]]

Constraints:

• groupSizes.length == n
• 1 <= n <= 500
• 1 <= groupSizes[i] <= n

class Solution{
    public List<List<Integer>> groupThePeople(int[] groupSizes){
        Map<Integer, List<Integer>> map = new HashMap<>();
        List<List<Integer>> result = new ArrayList<>();
        
        for(int i = 0; i < groupSizes.length; i++){
            int flag = groupSizes[i];
            if(! map.containsKey(flag))
                map.put(flag, new ArrayList<>());
            
            map.get(flag).add(i);
            
            if(map.get(flag).size() == flag){
                result.add(map.get(flag));
                map.remove(flag);
            }
        }
        return result;
    }
}

5281. Find the Smallest Divisor Given a Threshold

Medium

Given an array of integers nums and an integer threshold, we will choose a positive integer divisor and divide all the array by it and sum the result of the division. Find the smallest divisor such that the result mentioned above is less than or equal to threshold.

Each result of division is rounded to the nearest integer greater than or equal to that element. (For example: 7/3 = 3 and 10/2 = 5).

It is guaranteed that there will be an answer.

Example 1:

Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1. 
If the divisor is 4 we can get a sum to 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2). 

Example 2:

Input: nums = [2,3,5,7,11], threshold = 11
Output: 3

Example 3:

Input: nums = [19], threshold = 5
Output: 4

Constraints:

• 1 <= nums.length <= 5 * 10^4
• 1 <= nums[i] <= 10^6
• nums.length <= threshold <= 10^6

class Solution{
    public int smallestDivisor(int[] nums, int threshold){
        int lo = 1, hi = 1000000;

        while (lo < hi){
            int mid = (lo + hi) / 2;

            int result = cal(nums, mid);
            
            if(result > threshold)
                lo = mid + 1;
            else
                hi = mid;
        }
        return lo;
    }
    
    private int cal(int[] nums, int div){
        int sum = 0;
        for(int n : nums){
            sum += Math.ceil((double)n / (double)div);
            //if(n % div != 0) sum += 1;
        }
        return (int)sum;
    }
}

5282. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

Hard

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbours of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighboors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

Binary matrix is a matrix with all cells equal to 0 or 1 only.

Zero matrix is a matrix with all cells equal to 0.

Example 1:

Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We don't need to change it.

Example 3:

Input: mat = [[1,1,1],[1,0,1],[0,0,0]]
Output: 6

Example 4:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix can't be a zero matrix

Constraints:

• m == mat.length
• n == mat[0].length
• 1 <= m <= 3
• 1 <= n <= 3
• mat[i][j] is 0 or 1.