Your friendly python module
for scientific analysis and visualization of 3d objects.
pip install vedoadditional installation details [click to expand]
- To install the latest dev version of
vedo:
pip install -U git+https://github.com/marcomusy/vedo.git- To install from the conda-forge channel:
conda install -c conda-forge vedoThe webpage of the library with documentation is available here.
📌 Need help? Have a question, or wish to ask for a missing feature? Do not hesitate to ask any questions on the image.sc forum or by opening a github issue.
The library includes a large set of working examples for a wide range of functionalities
working with polygonal meshes and point clouds [click to expand]
- Import meshes from VTK format, STL, Wavefront OBJ, 3DS, Dolfin-XML, Neutral, GMSH, OFF, PCD (PointCloud),
- Export meshes as ASCII or binary to VTK, STL, OBJ, PLY ... formats.
- Analysis tools like Moving Least Squares, mesh morphing and more..
- Tools to visualize and edit meshes (cutting a mesh with another mesh, slicing, normalizing, moving vertex positions, etc..).
- Split mesh based on surface connectivity. Extract the largest connected area.
- Calculate areas, volumes, center of mass, average sizes etc.
- Calculate vertex and face normals, curvatures, feature edges. Fill mesh holes.
- Subdivide faces of a mesh, increasing the number of vertex points. Mesh simplification.
- Coloring and thresholding of meshes based on associated scalar or vectorial data.
- Point-surface operations: find nearest points, determine if a point lies inside or outside of a mesh.
- Create primitive shapes: spheres, arrows, cubes, torus, ellipsoids...
- Generate glyphs (associate a mesh to every vertex of a source mesh).
- Create animations easily by just setting the position of the displayed objects in the 3D scene. Add trailing lines and shadows to moving objects is supported.
- Straightforward support for multiple sync-ed or independent renderers in the same window.
- Registration (alignment) of meshes with different techniques.
- Mesh smoothing.
- Delaunay triangulation in 2D and 3D.
- Generate meshes by joining nearby lines in space.
- Find the closest path from one point to another, traveling along the edges of a mesh.
- Find the intersection of a mesh with lines, planes or other meshes.
- Interpolate scalar and vectorial fields with Radial Basis Functions and Thin Plate Splines.
- Add sliders and buttons to interact with the scene and the individual objects.
- Visualization of tensors.
- Analysis of Point Clouds
- Moving Least Squares smoothing of 2D, 3D and 4D clouds
- Fit lines, planes, spheres and ellipsoids in space
- Identify outliers in a distribution of points
- Decimate a cloud to a uniform distribution.
working with volumetric data and tetrahedral meshes
- Import data from VTK format volumetric TIFF stacks, DICOM, SLC, MHD and more
- Import 2D images as PNG, JPEG, BMP
- Isosurfacing of volumes
- Composite and maximum projection volumetric rendering
- Generate volumetric signed-distance data from an input surface mesh
- Probe volumes with lines and planes
- Generate stream-lines and stream-tubes from vectorial fields
- Slice and crop volumes
- Support for other volumetric structures (structured and grid data)
plotting and histogramming in 2D and 3D
- Polygonal 3D text rendering with Latex-like syntax and unicode characters, with 30 different fonts.
- Fully customizable axis styles
- donut plots and pie charts
- Scatter plots in 2D and 3D
- Surface function plotting
- 1D customizable histograms
- 2D hexagonal histograms
- Polar plots, spherical plots and histogramming
- Draw latex-formatted formulas in the rendering window.
- Quiver, violin, whisker and stream-line plots
- Graphical markers analogous to matplotlib
integration with other libraries
- Integration with the Qt5 framework.
- Support for FEniCS/Dolfin platform for visualization of PDE/FEM solutions.
- Interoperability with the trimesh, pyvista and pymeshlab libraries.
- Export 3D scenes and embed them into a web page.
- Embed 3D scenes in jupyter notebooks with K3D (can export an interactive 3D-snapshot page here).
Visualize a polygonal mesh or a volume from a terminal window simply with:
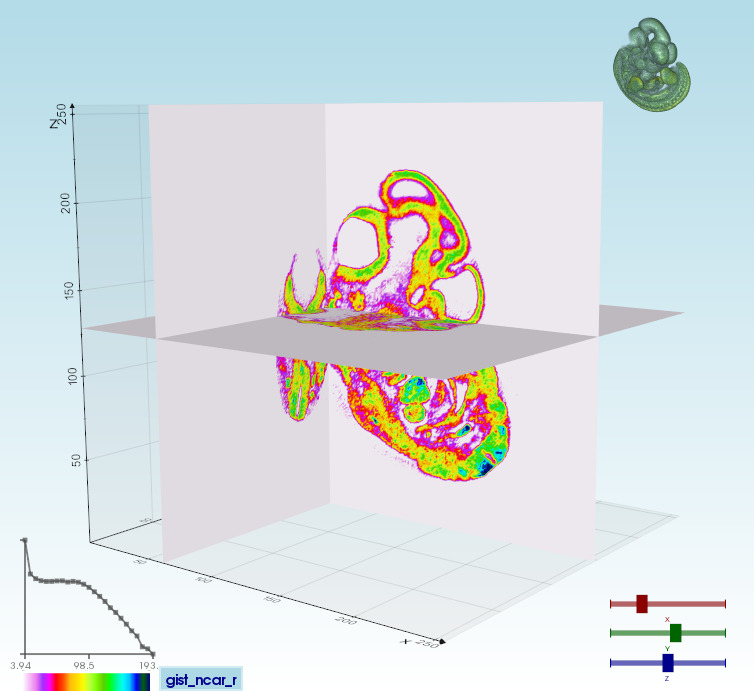
vedo https://vedo.embl.es/examples/data/embryo.tifvolumetric files (slc, tiff, DICOM...) can be visualized in different modes [click to expand]
Volume 3D slicingvedo --slicer embryo.slc |
Ray-castingvedo -g |
2D slicingvedo --slicer2d |
|---|---|---|
 |
 |
 |
Type vedo -h for the complete list of options.
vedo currently includes 300+ working examples and notebooks.
Run any of the built-in examples. In a terminal type: vedo -r warp2
Check out the example galleries organized by subject here:

Any contributions are greatly appreciated! If you have a suggestion that would make this better, please fork the repo and create a pull request. You can also simply open an issue with the tag "enhancement".
Scientific publications leveraging vedo:
- X. Diego et al.: "Key features of Turing systems are determined purely by network topology", Phys. Rev. X 8, 021071, DOI.
- M. Musy, K. Flaherty et al.: "A Quantitative Method for Staging Mouse Limb Embryos based on Limb Morphometry", Development (2018) 145 (7): dev154856, DOI.
- F. Claudi, A. L. Tyson, T. Branco, "Brainrender. A python based software for visualisation of neuroanatomical and morphological data.", eLife 2021;10:e65751, DOI.
- J. S. Bennett, D. Sijacki, "Resolving shocks and filaments in galaxy formation simulations: effects on gas properties and star formation in the circumgalactic medium", Monthly Notices of the Royal Astronomical Society, Volume 499, Issue 1, DOI.
- J.D.P. Deshapriya et al., "Spectral analysis of craters on (101955) Bennu". Icarus 2020, DOI.
- A. Pollack et al., "Stochastic inversion of gravity, magnetic, tracer, lithology, and fault data for geologically realistic structural models: Patua Geothermal Field case study", Geothermics, Volume 95, September 2021, DOI.
- X. Lu et al., "3D electromagnetic modeling of graphitic faults in the Athabasca Basin using a finite-volume time-domain approach with unstructured grids", Geophysics, DOI.
- M. Deepa Maheshvare et al., "A Graph-Based Framework for Multiscale Modeling of Physiological Transport", Front. Netw. Physiol. 1:802881, DOI.
- F. Claudi, T. Branco, "Differential geometry methods for constructing manifold-targeted recurrent neural networks", bioRxiv 2021.10.07.463479, DOI.
- J. Klatzow, G. Dalmasso, N. Martínez-Abadías, J. Sharpe, V. Uhlmann, "µMatch: 3D shape correspondence for microscopy data", Front. Comput. Sci., 15 February 2022. DOI
- G. Dalmasso et al., "4D reconstruction of murine developmental trajectories using spherical harmonics", Developmental Cell 57, 1–11 September 2022, DOI.
- D.J.E Waibel et al., "Capturing Shape Information with Multi-scale Topological Loss Terms for 3D Reconstruction", Lecture Notes in Computer Science, vol 13434. Springer, Cham. DOI.
- N. Lamb et al., "DeepJoin: Learning a Joint Occupancy, Signed Distance, and Normal Field Function for Shape Repair", ACM Transactions on Graphics (TOG), vol 41, 6, 2022. DOI
- J. Cotterell et al., "Cell 3D Positioning by Optical encoding (C3PO) and its application to spatial transcriptomics", bioRxiv 2024.03.12.584578; DOI
Have you found this software useful for your research? Star ✨ the project and cite it as:
M. Musy et al.,
"vedo, a python module for scientific analysis and visualization of 3D objects and point clouds",
Zenodo, 2021, doi: 10.5281/zenodo.7019968.



