This is a Java library that implements Principal Component Analysis (PCA) data transformation. It operates on data matrices where each row corresponds to a single real vector and each column corresponds to a single dimension.
The main use case of the library is to create a PCA transformation based on training data and then to apply it on test data. The library can perform two transformations on the test data:
- Rotation -- the data matrix is transformed to get a diagonal covariance matrix. This transformation is sometimes simply called PCA.
- Whitening -- the data matrix is transformed to get the unit covariance matrix.
The method deals with situations where some columns in the data matrix are linearly dependent or when there are more columns than rows in the data matrix i.e. there are more dimensions than samples in the data set. In such cases, the method discards some output space dimensions, or in other words a transformation is generated where the output vectors have fewer dimensions than the input ones. To handle situations where the columns are almost linearly dependent, we use a threshold parameter to discard dimensions with almost zero standard deviation; it set to a default value (tol = sqrt(.Machine$double.eps)) introduced in the help page of the prcomp function from the R statistical environment (see the part of the help page where the tol parameter is described). The .Machine$double.eps is the floating-point number machine precision from the R statistical environment (normally equal to 2.220446e-16)
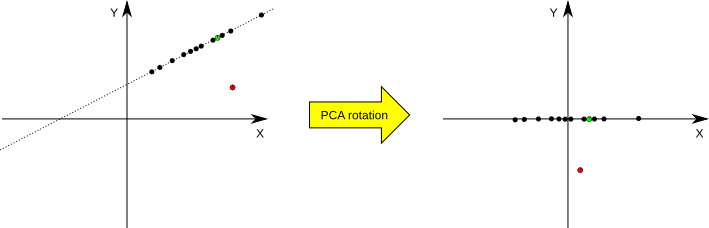
The library can be also used to check if given test point lies in the PCA-generated subspace. If it does not, it means that it does not belong to the transformation domain and can be treated as an outlier (see Fig.1 for an illustration). Here, we use the following practical rule to decide if a vector belongs to the domain. If the vector belongs to the domain space, its non-significant components (those with standard deviation equal 0) should be zeroed by the matrix transformation; if they are not, we assume that the vector is an outlier. We use a somewhat ad-hoc threshold to check if the values are different from zero (if the absolute value is smaller than the threshold, it is assumed to be zero). The threshold is equal to 3 * sqrt(.Machine$double.eps) * sd(PC1), where sqrt(.Machine$double.eps) is a value mentioned in the previous paragraph and sd(PC1) is a standard deviation of the first principal component.
Fig.1: An example of dimensionality reduction and outliers detection in PCA. On the left we have a situation before and on the right after the PCA transformation. The black dots correspond to two-dimensional samples from the training data set (situated on a single line) which are used to set the transformation parameters. The red point is an outlier point from the testing set, and the green point is a non-outlier point from the testing set. It can be seen that the two-dimensional samples from the training set are reduced to one-dimensional samples by the rotation transformation -- they all lay on the X axis now (their Y coordinate equals 0). The same goes for the green non-outlier point from the testing set. The red outlier point, on the other hand, does not have its Y coordinate equal 0.
Two methods of obtaining the transformation matrix are implemented. The first is based on the SVD and the second is based on the eigenvalue decomposition. The first one as the one more numerically stable is used by default.
The default SVD-based version of the algorithm is checked to return the same results as the implementation of the PCA from the R statistical environment -- the prcomp function (see the unit tests in the source code). Some columns of the transformed testing data matrix might be multiplied by -1 when compared with data returned by the R's prcomp. This is nothing to be worried about since both versions of the matrix are correct outputs of the PCA transformation and both are essentially equivalent as far as data processing applications are concerned.
Here is an example usage from one of the library's source files (src/main/java/com/mkobos/pca_transform/SampleRun.java):
package com.mkobos.pca_transform;
import Jama.Matrix;
/** An example program using the library */
public class SampleRun {
public static void main(String[] args){
System.out.println("Running a demonstration program on some sample data ...");
/** Training data matrix with each row corresponding to data point and
* each column corresponding to dimension. */
Matrix trainingData = new Matrix(new double[][] {
{1, 2, 3, 4, 5, 6},
{6, 5, 4, 3, 2, 1},
{2, 2, 2, 2, 2, 2}});
PCA pca = new PCA(trainingData);
/** Test data to be transformed. The same convention of representing
* data points as in the training data matrix is used. */
Matrix testData = new Matrix(new double[][] {
{1, 2, 3, 4, 5, 6},
{1, 2, 1, 2, 1, 2}});
/** The transformed test data. */
Matrix transformedData =
pca.transform(testData, PCA.TransformationType.WHITENING);
System.out.println("Transformed data (each row corresponding to transformed data point):");
for(int r = 0; r < transformedData.getRowDimension(); r++){
for(int c = 0; c < transformedData.getColumnDimension(); c++){
System.out.print(transformedData.get(r, c));
if (c == transformedData.getColumnDimension()-1) continue;
System.out.print(", ");
}
System.out.println("");
}
}
}
This results in the following output:
Running a demonstration program on some sample data ...
Transformed data (each row corresponding to transformed data point):
-0.9999999999999998, -0.5773502691896268
-0.08571428571428596, 1.732050807568878
This demonstration program can be run by executing the library's JAR file from the binary distribution package.
Since the library is deployed in Maven's Central Repository, if you use Maven build system, you can start using the library in your project after simply adding a dependency in your Maven POM file of the form of
<dependency>
<groupId>com.mkobos</groupId>
<artifactId>pca_transform</artifactId>
<version>XXX</version>
</dependency>
You can find the most current binary, source, and javadoc distributions of the library in Maven's Central Repository.
The source can be also retrieved straight from the Git repository: git clone git@github.com:mkobos/pca_transform.git.
The library is available under permissive MIT license (see file MIT-LICENSE.txt file for the text of the license).