Chebyshev polynomial of the second kind #78293
Conversation
[XLA hash update] update the pinned xla hash
🔗 Helpful links
✅ No Failures (0 Pending)As of commit d04bd3c (more details on the Dr. CI page): Expand to see more💚 💚 Looks good so far! There are no failures yet. 💚 💚 This comment was automatically generated by Dr. CI (expand for details).Please report bugs/suggestions to the (internal) Dr. CI Users group. |
0x00b1
requested review from
mruberry,
ngimel,
bdhirsh,
albanD,
anjali411 and
soulitzer
as code owners
|
heads up: prefer not to add ciflow/all, as it runs things that we are generally quite capacity constrained on. If you want to get signal on things that will be the cause of reverts, ciflow/trunk is sufficient |
|
Thanks @suo! I apologize for wasting resources. I will use trunk in the future. |
0x00b1
added
ciflow/trunk
|
@suo Should I be concerned about these failures? They don't appear to be relevant to this pull request. |
0x00b1
force-pushed
the
chebyshev-polynomial-u
branch
from
7f1c459 to
c6693e9
Compare
0x00b1
force-pushed
the
chebyshev-polynomial-u
branch
from
fcf3fe8 to
d04bd3c
Compare
|
@pytorchbot merge this please! |
|
Hey @0x00b1. |
Summary:
Adds:
```Python
chebyshev_polynomial_u(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the second kind $U_{n}(\text{input})$.
If $n = 0$, $1$ is returned. If $n = 1$, $2 \times \text{input}$ is returned. If $n < 6$ or $|\text{input}| > 1$ the recursion:
$$T_{n + 1}(\text{input}) = 2 \times \text{input} \times T_{n}(\text{input}) - T_{n - 1}(\text{input})$$
is evaluated. Otherwise, the explicit trigonometric formula:
$$\frac{\text{sin}((n + 1) \times \text{arccos}(\text{input}))}{\text{sin}(\text{arccos}(\text{input}))}$$
is evaluated.
## Derivatives
Recommended first derivative formula with respect to $\text{input}$:
$$\frac{(-1 - n)\times U_{-1 + n}(\text{input}) + n \times \text{input} \times U_{n}(x)}{-1 + \text{input}^{2}}.$$
Recommended $k$-derivative formula with respect to $\text{n}$:
$$\frac{\text{arccos}(\text{input})^{k} \times \text{sin}(\frac{k \times \pi}{2} + (1 + n) \times \text{arccos}(\text{input}))}{\sqrt{1 - \text{input}^{2}}}.$$
## Example
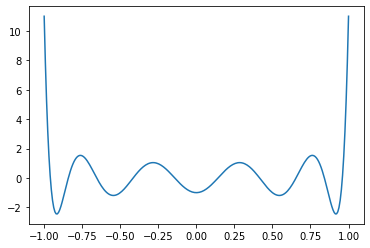
```Python
x = torch.linspace(-1.0, 1.0, 256)
matplotlib.pyplot.plot(x, torch.special.chebyshev_polynomial_u(x, 10))
```
Pull Request resolved: #78293
Approved by: https://github.com/mruberry
Test Plan: contbuild & OSS CI, see https://hud.pytorch.org/commit/pytorch/pytorch/40a6cc6cc640e6914b8160aea1399e4bb530213a
Reviewed By: seemethere
Differential Revision: D36783570
Pulled By: 0x00b1
fbshipit-source-id: d00ee06dadc0039166cc183768725833bbfb71e4
Adds:
Chebyshev polynomial of the second kind$U_{n}(\text{input})$ .
If$n = 0$ , $1$ is returned. If $n = 1$ , $2 \times \text{input}$ is returned. If $n < 6$ or $|\text{input}| > 1$ the recursion:
is evaluated. Otherwise, the explicit trigonometric formula:
is evaluated.
Derivatives
Recommended first derivative formula with respect to$\text{input}$ :
Recommended$k$ -derivative formula with respect to $\text{n}$ :
Example