This is an adaptation of Ninety-Nine Scala Problems by Phil Gold which itself is an adaptation of the Ninety-Nine Prolog Problems written by Werner Hett at the Berne University of Applied Sciences in Berne, Switzerland. Some problems have been altered to be more amenable to programming in Kotlin.
You might want to do these problems if you want to learn Kotlin, are interested in the problems described below, or both. The main reason to prefer this to using websites like hackerrank.com and codewars.com is that there is no vendor lock-in and no hidden agenda pursued by the website owner.
The suggested workflow is to solve a problem yourself and then compare solution to the one provided.
Solutions are available by clicking on the link at the beginning of the problem description.
Your goal should be to find the most elegant solution to the given problems.
Efficiency is important, but clarity is even more crucial.
Some of the (easy) problems can be trivially solved using built-in functions.
However, in these cases, you can learn more if you try to find your own solution.
The problems have different levels of difficulty.
Those marked with a single asterisk * are easy.
If you have successfully solved the preceding problems, you might be able to solve them within a few (say 15) minutes.
Problems marked with two asterisks ** are of intermediate difficulty and might take about 30-90 minutes to solve.
Problems marked with three asterisks *** are more difficult. You may need more time (i.e. a few hours or more) to find a good solution.
Please note that levels of difficulty is just a guess and assumes you are somewhat familiar with the problem domain.
It is perfectly ok if some of them take longer. Overall, the goal is to learn, not to finish "on time".
You might notice that there are less than 99 problems. This is because numbering of original problems was wrong. It was kept here for consistency with 99 problems in other programming languages.
The first 50 or so problems are easy. If this is boring for you, feel free to jump to Binary Trees.
All contributions are welcome (including alternative solutions for problems which already have a solution).
P01 (*) Find the last element of a list.
Example:
> last(listOf(1, 1, 2, 3, 5, 8))
8P02 (*) Find the last but one element of a list.
Example:
> penultimate(listOf(1, 1, 2, 3, 5, 8))
5P03 (*) Find the Nth element of a list.
By convention, the first element in the list is element 0.
Example:
> nth(2, listOf(1, 1, 2, 3, 5, 8))
2P04 (*) Find the number of elements of a list.
Example:
> length(listOf(1, 1, 2, 3, 5, 8))
6P05 (*) Reverse a list.
Example:
> reverse(listOf(1, 1, 2, 3, 5, 8))
[8, 5, 3, 2, 1, 1]P06 (*) Find out whether a list is a palindrome.
Example:
> isPalindrome(listOf(1, 2, 3, 2, 1))
trueP07 (*) Flatten a nested list structure.
Example:
> flatten(listOf(listOf(1, 1), 2, listOf(3, listOf(5, 8))))
[1, 1, 2, 3, 5, 8]P08 (*) Eliminate consecutive duplicates of list elements.
If a list contains repeated elements, they should be replaced with a single copy of the element. The order of the elements should not be changed. Example:
> compress("aaaabccaadeeee".toList())
[a, b, c, a, d, e]P09 (*) Pack consecutive duplicates of list elements into sublists.
If a list contains repeated elements, they should be placed in separate sublists. Example:
> pack("aaaabccaadeeee".toList())
[[a, a, a, a], [b], [c, c], [a, a], [d], [e, e, e, e]]P10 (*) Run-length encoding of a list.
Use the result of problem P09 to implement the so-called run-length encoding data compression method. Consecutive duplicates of elements are encoded as tuples (N, E) where N is the number of duplicates of the element E. Example:
> encode("aaaabccaadeeee".toList())
[(4, a), (1, b), (2, c), (2, a), (1, d), (4, e)]P11 (*) Modified run-length encoding.
Modify the result of problem P10 in such a way that if an element has no duplicates it is simply copied into the result list. Only elements with duplicates are transferred as (N, E) terms. Example:
> encodeModified("aaaabccaadeeee".toList())
[(4, a), b, (2, c), (2, a), d, (4, e)]P12 (*) Decode a run-length encoded list.
Given a run-length code list generated as specified in the problem P10, construct its uncompressed version. Example:
> decode(List((4, 'a), (1, 'b), (2, 'c), (2, 'a), (1, 'd), (4, 'e)))
[a, a, a, a, b, c, c, a, a, d, e, e, e, e]P13 (*) Run-length encoding of a list (direct solution).
Implement the so-called run-length encoding data compression method directly. I.e. don't use other methods you've written (like P09's pack); do all the work directly. Example:
> encodeDirect("aaaabccaadeeee".toList())
[(4, a), (1, b), (2, c), (2, a), (1, d), (4, e)]P14 (*) Duplicate the elements of a list.
Example:
> duplicate("abccd".toList())
[a, a, b, b, c, c, c, c, d, d]P15 (*) Duplicate the elements of a list a given number of times.
Example:
> duplicateN(3, "abccd".toList())
[a, a, a, b, b, b, c, c, c, c, c, c, d, d, d]P16 (*) Drop every Nth element from a list.
Example:
> drop(3, "abcdefghijk".toList())
[a, b, d, e, g, h, j, k]P17 (*) Split a list into two parts.
The length of the first part is given. Use a Pair for your result.
Example:
> split(3, "abcdefghijk".toList())
([a, b, c], [d, e, f, g, h, i, j, k])P18 (*) Extract a slice from a list.
Given two indices, I and K, the slice is the list containing the elements from and including the Ith element up to but not including the Kth element of the original list. Start counting the elements with 0. Example:
> slice(3, 7, "abcdefghijk".toList())
[d, e, f, g]P19 (*) Rotate a list N places to the left.
Examples:
> rotate(3, "abcdefghijk".toList())
[d, e, f, g, h, i, j, k, a, b, c]
> rotate(-2, "abcdefghijk".toList())
[j, k, a, b, c, d, e, f, g, h, i]P20 (*) Remove the Kth element from a list.
Return the list and the removed element in a Tuple. Elements are numbered from 0. Example:
> removeAt(1, "abcd".toList())
([a, c, d], b)P21 (*) Insert an element at a given position into a list.
Example:
> insertAt('X', 1, "abcd".toList())
[a, X, b, c, d]P22 (*) Create a list containing all integers within a given range.
Example:
> range(4, 9)
[4, 5, 6, 7, 8, 9]P23 (*) Extract a given number of randomly selected elements from a list.
Make sure there is a way to produce deterministic results. Example:
> randomSelect(3, "abcdefgh".toList())
[c, h, f]P24 (*) Lotto: Draw N different random numbers from the set 1..M.
Make sure there is a way to produce deterministic results. Example:
> lotto(3, 49)
[32, 28, 8]P25 (*) Generate a random permutation of the elements of a list.
Make sure there is a way to produce deterministic results. Hint: Use the solution of problem P23. Example:
> randomPermute("abcdef".toList())
[d, b, e, f, a, c]P26 (**) Generate the combinations of K distinct objects chosen from the N elements of a list.
In how many ways can a committee of 3 be chosen from a group of 12 people?
There are C(12,3) = 220 possibilities, where C(N,K) denotes binomial coefficient.
For pure mathematicians, this result may be great. But we want to really generate all the possibilities.
Example:
> combinations(3, "abcde".toList())
[[c, b, a], [d, b, a], [e, b, a], [d, c, a], [e, c, a], [e, d, a], [d, c, b], [e, c, b], [e, d, b], [e, d, c]]P27 (**) Group the elements of a set into disjoint subsets.
a) In how many ways can a group of 9 people work in 3 disjoint subgroups of 2, 3 and 4 persons? Write a function that generates all the possibilities. Example:
> group3(listOf("Aldo", "Beat", "Carla", "David", "Evi", "Flip", "Gary", "Hugo", "Ida"))
[[["Ida", "Hugo", "Gary", "Flip"], ["Evi", "David", "Carla"], ["Beat", "Aldo"]], ...b) Generalize the above predicate in a way that we can specify a list of group sizes and the predicate will return a list of groups. Example:
> group(listOf(2, 2, 5), listOf("Aldo", "Beat", "Carla", "David", "Evi", "Flip", "Gary", "Hugo", "Ida"))
[[["Ida", "Hugo", "Gary", "Flip", "Evi"], ["David", "Carla"], ["Beat", "Aldo"]], ...Note that we do not want permutations of the group members, i.e. [[Aldo, Beat], ...]] is the same solution as [[Beat, Aldo], ...].
However, [[Aldo, Beat], [Carla, David], ...] and [[Carla, David], [Aldo, Beat], ...] are considered to be different solutions.
You may find more about this combinatorial problem in a good book on discrete mathematics under the term multinomial coefficients.
P28 (*) Sorting a list of lists according to length of sublists.
a) We suppose that a list contains elements that are lists themselves. The objective is to sort elements of the list according to their length. E.g. short lists first, longer lists later, or vice versa. Example:
> lengthSort(listOf("abc".toList(), "de".toList(), "fgh".toList(), "de".toList(), "ijkl".toList(), "mn".toList(), "o".toList()))
[[o], [d, e], [d, e], [m, n], [a, b, c], [f, g, h], [i, j, k, l]]b) Again, we suppose that a list contains elements that are lists themselves. But this time the objective is to sort elements according to their length frequency; i.e. lists with rare lengths are placed first, others with more frequent lengths come later. Example:
> lengthFreqSort(listOf("abc".toList(), "de".toList(), "fgh".toList(), "de".toList(), "ijkl".toList(), "mn".toList(), "o".toList()))
[[i, j, k, l], [o], [a, b, c], [f, g, h], [d, e], [d, e], [m, n]]Note that in the above example, the first two lists in the result have length 4 and 1 and both lengths appear just once. The third and fourth lists have length 3 and there are two list of this length. Finally, the last three lists have length 2. This is the most frequent length.
> 7.isPrime()
trueP32 (*) Determine the greatest common divisor of two positive integer numbers.
Use Euclid's algorithm.
> gcd(36, 63)
9Two numbers are coprime if their greatest common divisor equals 1.
> 35.isCoprimeTo(64)
trueP34 (*) Calculate Euler's totient function phi(m).
Euler's so-called totient function phi(m) is defined as the number of positive integers r (1 <= r <= m) that are coprime to m.
> 10.totient()
4P35 (*) Determine prime factors of a given positive integer.
Construct a list containing prime factors in ascending order.
> 315.primeFactors()
[3, 3, 5, 7]P36 (*) Determine the prime factors of a given positive integer (2).
Construct a list containing prime factors and their multiplicity.
> 315.primeFactorMultiplicity()
[(3, 2), (5, 1), (7, 1)]P37 (*) Calculate Euler's totient function phi(m) (improved).
See problem P34 for the definition of Euler's totient function.
If the list of the prime factors of a number m is known in the form of problem P36,
then the function phi(m) can be efficiently calculated as follows:
Let [[p1, m1], [p2, m2], [p3, m3], ...] be the list of prime factors (and their multiplicities) of a given number m.
Then phi(m) can be calculated with the following formula:
phi(m) = (p1-1)*p1^(m1-1) * (p2-1)*p2^(m2-1) * (p3-1)*p3^(m3-1) * ...
P38 (*) Compare the two methods of calculating Euler's totient function.
Omitted. The assumption is that you already did the comparison, e.g. as unit test assertions.
P39 (*) A list of prime numbers.
Given a range of integers by its lower and upper limit, construct a list of all prime numbers in that range.
> listPrimesInRange(7..31)
[7, 11, 13, 17, 19, 23, 29, 31]P40 (*) Goldbach's conjecture.
Goldbach's conjecture
says that every positive even number greater than 2 is the sum of two prime numbers.
E.g. 28 = 5 + 23. It is one of the most famous facts in number theory that has not been proved to be correct
in the general case. It has been numerically confirmed up to very large numbers (much larger than Kotlin's Int can represent).
Write a function to find the two prime numbers that sum up to a given even integer.
> 28.goldbach()
(5, 23)P41 (*) A list of Goldbach compositions.
Given a range of integers by its lower and upper limit, print a list of all even numbers and their Goldbach composition.
> printGoldbachList(9..20)
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17In most cases, if an even number is written as the sum of two prime numbers, one of them is very small. Very rarely, the primes are both bigger than, say, 50. Example (minimum value of 50 for the primes):
> printGoldbachListLimited(2..3000, 50)
992 = 73 + 919
1382 = 61 + 1321
1856 = 67 + 1789
...P46 (*) Truth tables for logical expressions.
Define functions and_, or_, nand_, nor_, xor_, impl_, and equ_ (for logical equivalence)
which return true or false according to the result of their respective operations.
> true.and_(true)
true
> true.xor_(true)
falseWrite a function called printTruthTable which prints the truth table of a given logical expression.
> printTruthTable{ a, b -> a.and_(a.or_(b.not_())) }
a b result
true true true
true false true
false true false
false false falseFor Scala the task was to use implicit conversion. This is much simpler in Kotlin so the task omitted assuming it was done in the previous problem.
P48 (*) Truth tables for logical expressions (3).
Generalize problem 46 in such a way that the logical expression may contain any number of logical variables. Example:
> true.xor_(true, false, true)
trueP49 (*) Gray code.
An n-bit Gray code is a sequence of n-bit strings constructed according to certain rules. Find out the construction rules and write a function to generate Gray codes. For example:
> grayCodes(bits = 1)
[0, 1]
> grayCodes(bits = 2)
[00, 01, 11, 10]
> grayCodes(bits = 3)
[000, 001, 011, 010, 110, 111, 101, 100]P50 (**) Huffman code.
If you are not familiar with Huffman coding, consult internet (or a good book).
a) Given characters with their frequencies, e.g. {a=25, b=21, c=18, d=14, e=9, f=7, g=6}.
Our objective is to construct a Map, where key is character and value is the Huffman code for it.
> createEncoding(linkedMapOf(Pair('a', 25), Pair('b', 21), Pair('c', 18), Pair('d', 14), Pair('e', 9), Pair('f', 7), Pair('g', 6)))
{a=10, b=00, c=111, d=110, e=010, f=0111, g=0110}b) Write encode and decode functions for conversion between String and encoded String with zeroes and ones.
For example:
"this is a sentence".encode(encoding)
"00110000101011100101011101001110101111011001111011000111"
"00110000101011100101011101001110101111011001111011000111".decode(encoding)
"this is a sentence"A binary tree is either empty or it is composed of a root element and two successors, which are binary trees themselves.
We will use the following classes to represent binary trees (see Tree.kt).
An End is equivalent to an empty tree. A Node has a value, and two child trees.
The toString() functions are relatively arbitrary and were written to produce minimal readable output.
Note the usage of variance annotation
out T which makes classes covariant; it will be able to hold subtypes of whatever type it's created for.
End is declared as value because data classes
must have at least one constructor parameter.
End has type parameter of Nothing which is a subtype of every other type.
interface Tree<out T>
data class Node<out T>(val value: T, val left: Tree<T> = End, val right: Tree<T> = End) : Tree<T> {
override fun toString(): String {
val children = if (left == End && right == End) "" else " $left $right"
return "T($value$children)"
}
}
val End = object : Tree<Nothing>{
override fun toString() = "."
}The example of tree above can be written as:
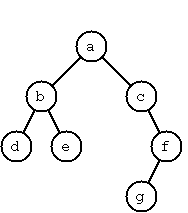
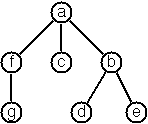
Node('a',
Node('b',
Node('d'),
Node('e')),
Node('c', End,
Node('f', Node('g'),
End)))A tree with only a root node would be Node('a') and an empty tree would be End.
Score one for static typing.
P55 (*) Construct completely balanced binary trees.
In a completely balanced binary tree, the following property holds for every node.
The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal,
which means their difference is not greater than one.
Define an object named Tree. Write a function balancedTrees to construct completely balanced binary trees for a given number of nodes.
The function should generate all solutions. The function should take as parameters the number of nodes and a single value to put in all of them.
> balancedTrees(4, "x")
[T(x T(x) T(x . T(x))), T(x T(x . T(x)) T(x)), T(x T(x) T(x T(x) .)), T(x T(x T(x) .) T(x))]P56 (*) Symmetric binary trees.
Let us call a binary tree symmetric if you can draw a vertical line through the root node and
then the right subtree is the mirror image of the left subtree.
Add an isSymmetric method to the Tree to check whether a given binary tree is symmetric.
Hint: Write isMirrorOf method first to check whether one tree is the mirror image of another.
We are only interested in the structure, not in the contents of the nodes.
> Node("a", Node("b"), Node("c")).isSymmetric()
trueP57 (*) Binary search trees (dictionaries).
Write a function to add an element to a binary search tree.
> End.add(2)
T(2)
> res0.add(3)
T(2 . T(3))
> res1.add(0)
T(2 T(0) T(3))Note that definition of add should have T : Comparable<T> type constraint
to allows us to use the < operator on the values in the tree.
Use that function to construct a binary tree from a list of integers.
> listOf(3, 2, 5, 7, 1).toTree()
T(3 T(2 T(1) .) T(5 . T(7)))Finally, use isSymmetric() from P56 to check conversion to tree.
> listOf(5, 3, 18, 1, 4, 12, 21).toTree().isSymmetric()
true
> listOf(3, 2, 5, 7, 4).toTree().isSymmetric()
falseP58 (*) Generate-and-test paradigm.
Apply the generate-and-test paradigm to construct all symmetric, completely balanced binary trees with a given number of nodes.
> symmetricBalancedTrees(5, "x")
[T(x T(x . T(x)) T(x T(x) .)), T(x T(x T(x) .) T(x . T(x)))]P59 (**) Construct height-balanced binary trees.
In a height-balanced binary tree, the following property holds for every node:
The height of its left subtree and the height of its right subtree are almost equal, which means their difference is not greater than one.
Write a method heightBalancedTrees to construct height-balanced binary trees for a given height with a supplied value for the nodes.
The function should generate all solutions.
> heightBalancedTrees(3, "x")
[T(x T(x T(x) T(x)) T(x T(x) T(x))), T(x T(x T(x) T(x)) T(x T(x) .)), ...]P60 (**) Construct height-balanced binary trees with a given number of nodes.
Consider a height-balanced binary tree of height H.
The maximum number of nodes it can contain is MaxN = 2**H - 1.
However, what is the minimum number MinN? This question is more difficult.
Try to find a recursive statement and turn it into a function minNodeAmountInHBTree that takes a height and returns MinN.
> minNodeAmountInHBTree(height = 3)
4On the other hand, we might ask: what is the maximum height H a height-balanced binary tree with N nodes can have?
Write a maxHeightOfHBTree function.
> maxHeightOfHBTree(nodeAmount = 4)
3Now, we can attack the main problem: construct all the height-balanced binary trees with a given number of nodes.
> allHBTreesWithNodeAmount(4, "x")
[T(x T(x T(x) .) T(x)), T(x T(x . T(x)) T(x)), ...]Find out how many height-balanced trees exist for N = 15.
P61 (*) Leaves and internal nodes of a binary tree.
A leaf is a node with no successors.
Write a method leafCount to count them.
> Node("x", Node("x"), End).leafCount()
1Write a method leafValues to collect leaf values into a list.
> Node("a", Node("b"), Node("c", Node("d"), Node("e"))).leafValues()
[b, d, e]An internal node of a binary tree has either one or two non-empty successors.
Write a method internalValues to collect their values into a list.
> Node("a", Node("b"), Node("c", Node("d"), Node("e"))).internalValues()
[a, c]P62 (*) Collect nodes at a given level in a list.
A node of a binary tree is at level N if the path from the root to the node has length N-1.
The root node is at level 1. Write a method valuesAtLevel to collect all node values at a given level into a list.
> Node('a', Node('b'), Node('c', Node('d'), Node('e'))).valuesAtLevel(2)
[b, c]Using valuesAtLevel it is easy to construct a method to create the level-order sequence of the nodes.
However, there are more efficient ways to do that.
P63 (*) Construct a complete binary tree.
A complete binary tree with height H is defined as follows:
The levels 1,2,3,...,H-1 contain the maximum number of nodes, i.e 2(i-1) nodes at the level i (note that we start counting the levels from 1 at the root).
At level H, which may contain less than the maximum possible number of nodes, all the nodes are "left-adjusted".
This means that in a level-order tree traversal all internal nodes come first, the leaves come second,
and empty successors (the Ends which are not really nodes) come last.
Particularly, complete binary trees are used as data structures (or addressing schemes) for heaps.
We can assign an address number to each node in a complete binary tree by enumerating the nodes in level order,
starting at the root with number 1. In doing so, we realize that for every node X with address A the following property holds:
The address of X's left and right children are 2*A and 2*A+1 (assuming the children exist).
This fact can be used to elegantly construct a complete binary tree structure.
Write a method completeBinaryTree that takes as parameters the number of nodes and the value to put in each node.
> completeBinaryTree(6, "x")
T(x T(x T(x) T(x)) T(x T(x) .))P64 (**) Layout a binary tree (1).
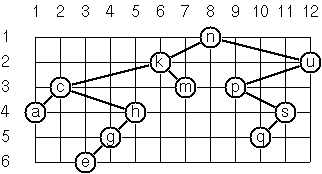
As a preparation for drawing a tree, a layout algorithm is required to determine the position of each node in a rectangular grid.
Several layout methods are conceivable, one of them is shown in the illustration below.
This tree can be constructed with "nkmcahgeupsq".toList().toTree().
In this layout strategy, the position of a node v is obtained by the following two rules:
x(v)is equal to the position of the nodevin the in-order sequencey(v)is equal to the depth of the nodevin the tree In order to store the position of the nodes, we add a new data classes with the additional information.
data class Point(val x: Int, val y: Int)
data class Positioned<out T>(val value: T, val point: Point) {
constructor (value: T, x: Int, y: Int) : this(value, Point(x, y))
override fun toString(): String =
"[" + point.x.toString() + "," + point.y.toString() + "] " + value.toString()
}Write a method layout that turns a tree of normal Nodes into a tree with positions Tree<Positioned<T>>.
> Node("a", Node("b", End, Node("c")), Node("d")).layout()
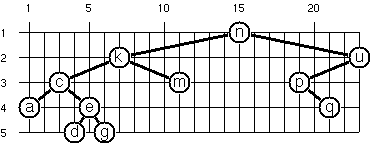
T([3,1] a T([1,2] b . T([2,3] c)) T([4,2] d))P65 (**) Layout a binary tree (2).
An alternative layout method is depicted in the illustration below
(note that it is not the same tree as in the previous problem).
This tree can be constructed with "nkmcaedgupq".toList().toTree().
Find out the rules and write the corresponding method. Hint: On a given level, the horizontal distance between neighboring nodes is constant. Use the same conventions as in the problem P64.
> Node("a", Node("b", End, Node("c")), Node("d")).layout2()
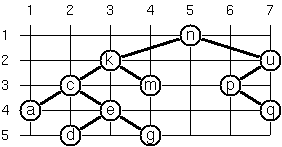
T[3,1]('a T[1,2]('b . T[2,3]('c . .)) T[5,2]('d . .))P66 (***) Layout a binary tree (3).
Yet another layout strategy is shown in the illustration below.
This tree can be constructed with "nkmcaedgupq".toList().toTree().
The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding method. Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree? Use the same conventions as in problem P64 and P65. Note: This is a difficult problem. Don't give up too early!
> Node('a', Node('b', End, Node('c')), Node('d')).layoutBinaryTree3()
T[2,1]('a T[1,2]('b . T[2,3]('c . .)) T[3,2]('d . .))Which layout do you like most?
P67 (**) A string representation of binary trees.
Binary trees can be represented as strings of the following type:
a(b(d,e),c(,f(g,))).
Write a method which generates this string representation given tree as Nodes and Ends.
And a method which does this inverse, i.e. given the string representation, construct the tree in the usual form.
> Node("a", Node("b", Node("d"), Node("e")), Node("c", End, Node("f", Node("g"), End))).convertToString()
a(b(d,e),c(,f(g,)))
> "a(b(d,e),c(,f(g,)))".convertToTree()
T(a T(b T(d) T(e)) T(c . T(f T(g) .)))P68 (**) Preorder and inorder sequences of binary trees.
a) Write methods preorder and inorder that construct the pre-order and in-order sequence of a given binary tree, respectively.
The results should be lists, e.g. ["a","b","d","e","c","f","g"] for the preorder sequence of the example in problem
P67.
> "a(b(d,e),c(,f(g,)))".convertToTree().preorder()
[a, b, d, e, c, f, g]
> "a(b(d,e),c(,f(g,)))".convertToTree().inorder()
[d, b, e, a, c, g, f]b) If both the preorder sequence and the in-order sequence of the nodes of a binary tree are given,
then the tree is determined unambiguously. Write a method createTree that does the job.
> createTree(preorder = listOf("a", "b", "d", "e", "c", "f", "g"), inorder = listOf("d", "b", "e", "a", "c", "g", "f"))
a(b(d,e),c(,f(g,)))What happens if the same character appears in more than one node? Try, for instance:
createTree(preorder = listOf("a", "b", "a"), inorder = listOf("b", "a", "a"))P69 (*) Dot-string representation of binary trees.
Binary tree in which leaves contain only single characters can be represented by the preorder sequence of its nodes
in which dots . are inserted where an empty subtree End is encountered during tree traversal.
For example, the tree shown in problem P67 is represented as abd..e..c.fg....
First, try to establish a syntax (BNF or syntax diagrams)
and then write two methods, toDotString and fromDotString, which do the conversion in both directions.
> "a(b(d,e),c(,f(g,)))".convertToTree().toDotString()
abd..e..c.fg...
> "abd..e..c.fg...".fromDotString()
a(b(d,e),c(,f(g,)))A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.
The code to represent multiway-trees is somewhat simpler than the code for binary trees, partly because we don't separate classes for nodes and terminators, and partly because we don't need the restriction for the value type to be ordered.
data class MTree<out T>(val value: T, val children: List<MTree<T>> = emptyList()) {
constructor(value: T, vararg children: MTree<T>): this(value, children.toList())
override fun toString(): String =
if (children.isEmpty()) value.toString()
else value.toString() + " {" + children.joinToString(", "){ it.toString() } + "}"
} The example tree is, thus:
MTree("a",
MTree("f",
MTree("g")),
MTree("c"),
MTree("b",
MTree("d"), MTree("e"))
))
The starting code for this section is in MTree.kt.
P70A (*) Count the nodes of a multiway tree.
Write a method nodeCount which counts the nodes of a given multiway tree.
> MTree("a", MTree("f")).nodeCount()
2P70B (*) Tree construction from a node string.
Suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes,
a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level.
By this rule, the tree in the following figure is represented as: afg^^c^bd^e^^^.
Define the syntax of the string and write a function convertToMTree to construct an MTree from a String.
Write the reverse convertToString function.
> MTree('a', MTree('f', MTree('g')), MTree('c'), MTree('b', MTree('d'), MTree('e'))).toString()
afg^^c^bd^e^^^P71 (*) Determine the internal path length of a tree.
We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree.
By this definition, the tree in the figure of problem P70B
has an internal path length of 9. Write a method internalPathLength to return that sum.
> "afg^^c^bd^e^^^".convertToMTree().internalPathLength()
9P72 (*) Construct the postorder sequence of the tree nodes.
Write a method postorder which constructs the postorder sequence of the node values of a multiway tree.
The result should be a List.
> "afg^^c^bd^e^^^".convertToMTree().postorder()
[g, f, c, d, e, b, a]P73 (**) Lisp-like tree representation.
Lisp is a prominent functional programming language.
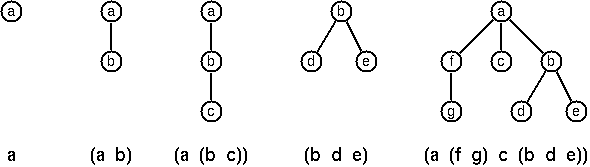
In Lisp almost everything is a list. Our example tree would be represented in Lisp as (a (f g) c (b d e)).
The following pictures give some more examples.
Note that in the Lisp notation a node with successors (children) in the tree is always the first element in a list, followed by its children.
The "lispy" representation of a multiway tree is a sequence of atoms and parentheses ( and ), with the atoms separated by spaces.
a) Write a method toLispString which constructs a "lispy" String from an MTree.
> MTree("a", MTree("b", MTree("c"))).toLispString()
(a (b c))b) As a second, even more interesting, exercise try to write a method that takes a "lispy" string and turns it into a multiway tree.
> "(a (f g) c (b d e))".fromLispString()
a {f {g}, c, b {d, e}}(Warning! The introductory text below is quite long. If you are familiar with graphs, you might just look at source code in Graph.kt.)
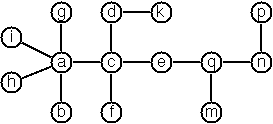
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of nodes.
The class to represent a graph is mutable, which isn't in keeping with pure functional programming, but a pure functional data structure would make things much, much more complicated. Pure functional graphs with cycles require laziness; Kotlin can probably handle it, but I think that would add too much of a barrier to the following questions.
Our graphs use an incidence list internally. Each has a list of nodes and a list of edges. Each node also has a list of edges that connect it to other nodes. In a directed graph, nodes, that are the target of arcs, do not have references to those arcs in their adjacency list.
class Graph<T, U> {
val nodes: MutableMap<T, Node<T, U>> = HashMap()
val edges: MutableList<Edge<T, U>> = ArrayList()
fun addNode(value: T): Node<T, U> {
val node = Node<T, U>(value)
nodes.put(value, node)
return node
}
fun addUndirectedEdge(n1: T, n2: T, label: U?) {
if (!nodes.contains(n1) || !nodes.contains(n2)) {
throw IllegalStateException("Expected '$n1' and '$n2' nodes to exist in graph")
}
val edge = UndirectedEdge(nodes[n1]!!, nodes[n2]!!, label)
if (edges.all{ !it.equivalentTo(edge) }) {
edges.add(edge)
nodes[n1]!!.edges.add(edge)
nodes[n2]!!.edges.add(edge)
}
}
fun addDirectedEdge(source: T, dest: T, label: U?) {
val edge = DirectedEdge(nodes[source]!!, nodes[dest]!!, label)
if (!edges.contains(edge)) {
edges.add(edge)
nodes[source]!!.edges.add(edge)
}
}
data class Node<T, U>(val value: T) {
val edges: MutableList<Edge<T, U>> = ArrayList()
fun neighbors(): List<Node<T, U>> = edges.map{ edge -> edge.target(this)!! }
override fun toString() = value.toString()
}
interface Edge<T, U> {
val n1: Node<T, U>
val n2: Node<T, U>
val label: U?
fun target(node: Node<T, U>): Node<T, U>?
fun equivalentTo(other: Edge<T, U>) =
(n1 == other.n1 && n2 == other.n2) || (n1 == other.n2 && n2 == other.n1)
}
data class UndirectedEdge<T, U>(override val n1: Node<T, U>, override val n2: Node<T, U>, override val label: U?) : Edge<T, U> {
override fun target(node: Node<T, U>) = if (n1 == node) n2 else if (n2 == node) n1 else null
override fun toString() = n1.toString() + "-" + n2 + (if (label == null) "" else "/" + label.toString())
}
data class DirectedEdge<T, U>(override val n1: Node<T, U>, override val n2: Node<T, U>, override val label: U?) : Edge<T, U> {
override fun target(node: Node<T, U>) = if (n1 == node) n2 else null
override fun toString() = n1.toString() + ">" + n2 + (if (label == null) "" else "/" + label.toString())
}
}
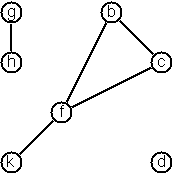
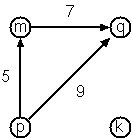
There are a few ways to create a graph from primitives. The graph-term form lists the nodes and edges separately:
Graph.terms(TermForm(
nodes = listOf("b", "c", "d", "f", "g", "h", "k"),
edges = listOf(Term("b", "c"), Term("b", "f"), Term("c", "f"), Term("f", "k"), Term("g", "h"))))The adjacency-list form associates each node with its adjacent nodes. In an undirected graph, care must be taken to ensure
that all links are symmetric, i.e. if b is adjacent to c, c must also be adjacent to b.
Graph.adjacent(AdjacencyList(
Entry("b", links("c", "f")),
Entry("c", links("b", "f")),
Entry("d"),
Entry("f", links("b", "c", "k")),
Entry("g", links("h")),
Entry("h", links("g")),
Entry("k", links("f"))))The representations we introduced so far are bound to our implementation and therefore well suited for automated processing,
but their syntax is not very user-friendly. Typing the terms by hand is cumbersome and error-prone.
We can define a more compact and "human-friendly" notation as follows:
A graph is represented by a string of terms of the type X or Y-Z separated by commas.
The standalone terms stand for isolated nodes, the Y-Z terms describe edges.
If an X appears as an endpoint of an edge, it is automatically defined as a node.
Our example could be written as:
[b-c, f-c, g-h, f-b, k-f, h-g, d]
We call this the human-friendly form. As the example shows, the list does not have to be sorted
and may even contain the same edge multiple times. Notice the isolated node d.
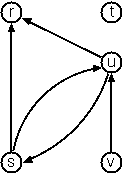
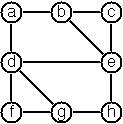
Directed graph is a graph where edges have direction. To represent a directed graph, the forms discussed above are slightly modified. The example graph is represented as follows:
In graph-term form:
Graph.directedTerms(TermForm(
listOf("r", "s", "t", "u", "v"),
listOf(Term("s", "r"), Term("s", "u"), Term("u", "r"), Term("u", "s"), Term("v", "u"))))In adjacency-list form (note that the adjacency-list form is the same for graphs and digraphs):
Graph.directedAdjacent(AdjacencyList(
Entry("r"),
Entry("s", links("r", "u")),
Entry("t"),
Entry("u", links("r", "s")),
Entry("v", links("u"))))Human-friendly form:
[s>r, s>u, u>r, u>s, v>u, t]
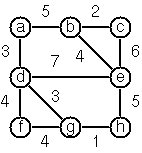
Finally, graphs with additional information attached to edges are called labeled graphs.
Graph-term form:
Graph.labeledTerms(TermForm(
listOf("k", "m", "p", "q"),
listOf(Term("m", "q", 7), Term("p", "m", 5), Term("p", "q", 9))))Adjacency-list form:
Graph.labeledDirectedAdjacent(AdjacencyList(
Entry("k"),
Entry("m", Link("q", 7)),
Entry("p", Link("m", 5), Link("q", 9)),
Entry("q")))Human-friendly form:
[m-q/7, p-m/5, p-q/9, k]
The notation for labeled graphs can also be used for so-called multi-graphs, where more than one edge is allowed between two given nodes.
P80 (*) Conversions.
Write String.toGraph() and String.toLabeledGraph() functions to create graphs from strings
(you can detect if graph is labeled or unlabeled based on input string format).
Write functions toTermForm and toAdjacencyList to generate the graph-term and adjacency-list forms of a Graph.
> "[b-c, b-f, c-f, f-k, g-h, d]".toGraph().toTermForm()
TermForm(nodes=[f, g, d, b, c, k, h], edges=[Term(b, c), Term(b, f), Term(c, f), Term(f, k), Term(g, h)])
> "[m>q/7, p>m/5, p>q/9, k]".toLabeledGraph().toAdjacencyList()
AdjacencyList(Entry("q"), Entry("p", listOf(Link("q", 9), Link("m", 5))), Entry("m", listOf(Link("q", 7))), Entry("k"))P81 (***) Path between nodes.
a) Write method findAllPaths to find acyclic paths from one node to another in a graph.
The method should return all paths.
> "[p>q/9, m>q/7, k, p>m/5]".toLabeledGraph().findAllPaths("p", "q")
[[p, q], [p, m, q]]
> "[p>q/9, m>q/7, k, p>m/5]".toLabeledGraph().findAllPaths("p", "k")
[]b) Write method findShortestPath to find shortest path between two nodes.
Hint: use Dijkstra or A* algorithm.
"[a-b/1, b-c/1, a-c/3]".toLabeledGraph().findShortestPath("a", "c")
[a, b, c]P82 (*) Cycles from a node.
Write a method named findCycles to find closed paths (cycles) starting at a given node in a graph.
The method should return all cycles. (Note that single edge doesn't count as a cycle.)
> "[a-b]".toGraph().findCycles("a")
[]
> "[b-c, b-f, c-f, f-k, g-h, d]".toGraph().findCycles("f")
[[f, c, b, f], [f, b, c, f]]P83 (**) Spanning trees.
Write a method spanningTrees to construct all spanning trees of a given graph.
When you have a correct solution for the spanningTrees method,
use it to define two other useful methods: Graph.isTree and Graph.isConnected.
> "[a-b, b-c, a-c]".toGraph().spanningTrees()
[[a-b, b-c], [a-b, c-a], [b-c, c-a]]
> "[a-b, b-c, a-c]".toGraph().isTree()
false
> "[a-b, b-c, a-c]".toGraph().isConnected()
trueFind out how many spanning trees there are for the graph depicted below.
"[a-b, a-d, b-c, b-e, c-e, d-e, d-f, d-g, e-h, f-g, g-h]".toGraph()P84 (**) Minimum spanning tree.
Write a method minSpanningTree to construct the minimum spanning tree
of a given labeled graph. Hint: Use Prim's Algorithm.
> "[a-b/1, b-c/2, a-c/3]".toLabeledGraph().minSpanningTree()
[a-b/1, b-c/2]Find minimum spanning tree for the graph below:
"[a-b/5, a-d/3, b-c/2, b-e/4, c-e/6, d-e/7, d-f/4, d-g/3, e-h/5, f-g/4, g-h/1]".toLabeledGraph()P85 (**) Graph isomorphism.
Two graphs G1(N1,E1) and G2(N2,E2) are isomorphic
if there is a bijection f: N1 → N2
such that for any nodes X,Y of N1, X and Y are adjacent if and only if f(X) and f(Y) are adjacent.
Write a method that determines whether two graphs are isomorphic.
> "[a-b]".toGraph().isIsomorphicTo("[5-7]".toGraph())
true
> "[a-b, b-c]".toGraph().isIsomorphicTo("[1-2, 3]".toGraph())
false
> "[a-b, b-c, c-d, d-a]".toGraph().isIsomorphicTo("[1-2, 2-3, 3-4, 4-1]".toGraph()
trueP86 (**) Node degree and graph coloration.
a) Write a method Node.degree that determines the degree
of a given node in an undirected graph.
> "[a-b, b-c, a-c, a-d]".toGraph().nodes["a"].degree()
3b) Use Welsh-Powell's algorithm
to paint the nodes of an undirected graph in such a way that adjacent nodes have different colors.
Write a method colorNodes that returns a list of tuples, each of which contains a node and an integer representing its color.
> "[a-b, b-c, a-c, a-d]".toGraph().colorNodes()
[(a,1), (b,2), (c,3), (d,2)]P87 (**) Depth-first order graph traversal.
a) Write a method that generates a depth-first order graph traversal sequence. The starting point should be specified, and the output should be a list of nodes that are reachable from this starting point (in depth-first order).
> "[a-b, b-c, c-d, d-e]".toGraph().nodesByDepthFrom("c")
[c, b, a, d, e]b) Write similar method for breadth-first graph traversal.
> "[a-b, b-c, c-d, d-e]".toGraph().nodesByBreadthFrom("c")
[c, b, d, a, e]P88 (*) Connected components.
Write a function that splits a graph into its connected components.
> "[a-b, c-d]".toGraph().components()
[[a-b], [c-d]]P89 (**) Bipartite graphs.
Write a function that determines whether a given graph is bipartite.
> "[a-b, b-c]".toGraph().isBipartite()
true
> "[a-b, b-c, c-a]".toGraph().isBipartite()
false
> "[a-b, b-c, d]".toGraph().isBipartite()
true
> "[a-b, b-c, d, e-f, f-g, g-e, h]".toGraph().isBipartite()
false
> "[a>b, c>a, d>b]".toGraph().isBipartite()
trueP90 (**) Eight queens.
This is a classical problem in computer science. The objective is to place eight queens on a chessboard so that no two queens are attacking each other, i.e. no two queens are in the same row, column or diagonal.
Hint: it might be easier to represent positions of the queens as a list of numbers 1..N.
For example, listOf(4, 2, 7, 3, 6, 8, 5, 1) meaning that queen in the first column is in row 4,
the queen in the second column is in row 2, etc. Otherwise, feel free to use a data class for queen position.
P91 (**) Knight's tour.
This is another classical problem in computer science.
How can a knight jump on an N×N chessboard in such a way that it visits every square exactly once?
Write a function knightsTours(N, (X, Y)) to list all knight tours that be made from (X, Y) on a N×N chessboard.
Hints: It might help to represent squares by pairs of their coordinates of the form Pair(X, Y),
where X and Y are integers between 0 and N-1. Alternatively, define a Point data class for this purpose.
Can you find only "closed tours", where the knight can jump from its final position back to its starting position? Can you make a lazy list that only calculates the tours as needed?
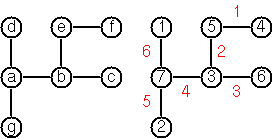
P92 (***) Von Koch's conjecture (see also graceful labeling).
Several years ago I met a mathematician who was intrigued by a problem for which he didn't know a solution. His name was Von Koch, and I don't know whether the problem has been solved since. (The "I" here refers to the author of the Prolog problems.)
Anyway the puzzle goes like this: Given a tree with N nodes (and hence N-1 edges),
find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way,
that for each edge K the difference of its node numbers is equal to K.
The conjecture is that this is always possible.
For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don't know for sure whether there is always a solution!
Write a function that calculates a numbering scheme for a given tree. What is the solution for the larger tree pictured below?
P93 (***) An arithmetic puzzle.
Given a list of integer numbers, find a correct way of inserting arithmetic operators +-*/() such that the result is a correct equation.
Example: With the list of numbers 2, 3, 5, 7, 11 we can form the equations 2 - 3 + 5 + 7 = 11, 2 = (3 * 5 + 7) / 11 and others.
P94 (***) Regular graphs with N nodes.
In a K-regular graph all nodes have a degree of K, i.e. the number of edges incident in each node is K.
Write a function to find all non-isomorphic 3-regular graphs with 6 nodes.
P95 (**) English number words.
On financial documents, like checks, numbers must sometimes be written in full words.
For example, 175 will be written as one hundred seventy five.
Write a function Int.toWords() to convert (non-negative) integer numbers to words.
P96 (**) Conway's Game of Life.
The Game of Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.
The game is represented by a 2-dimensional grid populated with cells. Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:
- Any live cell with fewer than two live neighbours dies, as if caused by under-population.
- Any live cell with two or three live neighbours lives on to the next generation.
- Any live cell with more than three live neighbours dies, as if by over-population.
- Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.
Note that there are certain patterns which can keep cells alive forever. See examples of patterns on Wikipedia.
Write a program to simulate evolution of cells in The Game of Life.
Sudoku puzzles go like this:
Problem Solution
..4|8..|.17 934|825|617
67.|9..|... 672|914|853
5.8|.3.|..4 518|637|924
---+---+--- ---+---+---
3..|74.|1.. 325|748|169
.69|...|78. 469|153|782
..1|.69|..5 781|269|435
---+---+--- ---+---+---
1..|.8.|3.6 197|582|346
...|..6|.91 853|476|291
24.|..1|5.. 246|391|578
Every cell in the puzzle belongs to a (horizontal) row and a (vertical) column, as well as to one single 3×3 square.
At the beginning, some of the cells carry a single-digit number between 1 and 9.
The problem is to fill the missing cells with digits in such a way that every number between 1 and 9 appears exactly once in each row,
in each column, and in each square.
Around 1994, a certain kind of puzzles was very popular in England. The "Sunday Telegraph" newspaper wrote: "Nonograms are puzzles from Japan and are currently published each week only in The Sunday Telegraph. Simply use your logic and skill to complete the grid and reveal a picture or diagram." As a programmer, you are in a better situation: you can have your computer do the work! Just write a little program ;-)
Each row and column of a rectangular bitmap is annotated with the respective lengths of its distinct strings of occupied cells. The person who solves the puzzle must complete the bitmap given only these lengths.
Problem Solution
|_|_|_|_|_|_|_|_| 3 |_|X|X|X|_|_|_|_| 3
|_|_|_|_|_|_|_|_| 2 1 |X|X|_|X|_|_|_|_| 2 1
|_|_|_|_|_|_|_|_| 3 2 |_|X|X|X|_|_|X|X| 3 2
|_|_|_|_|_|_|_|_| 2 2 |_|_|X|X|_|_|X|X| 2 2
|_|_|_|_|_|_|_|_| 6 |_|_|X|X|X|X|X|X| 6
|_|_|_|_|_|_|_|_| 1 5 |X|_|X|X|X|X|X|_| 1 5
|_|_|_|_|_|_|_|_| 6 |X|X|X|X|X|X|_|_| 6
|_|_|_|_|_|_|_|_| 1 |_|_|_|_|X|_|_|_| 1
|_|_|_|_|_|_|_|_| 2 |_|_|_|X|X|_|_|_| 2
1 3 1 7 5 3 4 3 1 3 1 7 5 3 4 3
2 1 5 1 2 1 5 1
For the example above, the problem can be stated as the two lists [[3],[2,1],[3,2],[2,2],[6],[1,5],[6],[1],[2]] and
[[1,2],[3,1],[1,5],[7,1],[5],[3],[4],[3]] which give the "solid" lengths of the rows and columns, top-to-bottom and left-to-right,
respectively. Published puzzles are larger than this example, e.g. 25×20, and always have unique solutions.
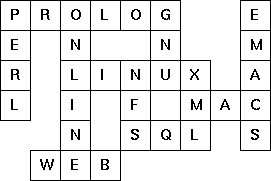
P99 (***) Crossword puzzle.
Given an empty (or almost empty) framework of a crossword puzzle and a set of words the problem is to place the words into the framework.
The particular crossword puzzle is specified in a text file which first lists the words (one word per line) in an arbitrary order.
Then, after an empty line, the crossword framework is defined. In this framework specification, an empty character location is represented
by a dot .. In order to make the solution easier, character locations can also contain predefined character values.
The crossword showed below is defined in the file p99a.dat, other examples are p99b.dat and p99d.dat.
There is also an example of a puzzle (p99c.dat) which does not have a solution.
Content of p99a.dat:
LINUX
PROLOG
PERL
ONLINE
GNU
XML
NFS
SQL
EMACS
WEB
MAC
...... .
. . . .
. ..... .
. . . ...
. ... .
...
Words are strings of at least two characters. A horizontal or vertical sequence of character places in the crossword puzzle framework is called a site. Our problem is to find a compatible way of placing words onto sites.
E.g. something like Sentient Language 😄