Probabilistic Roadmaps (PRM)

Clone into directory and Run using python3 prm.py

A probabilistic roadmap (PRM) is a network graph of possible paths in a given map based on free and occupied spaces.

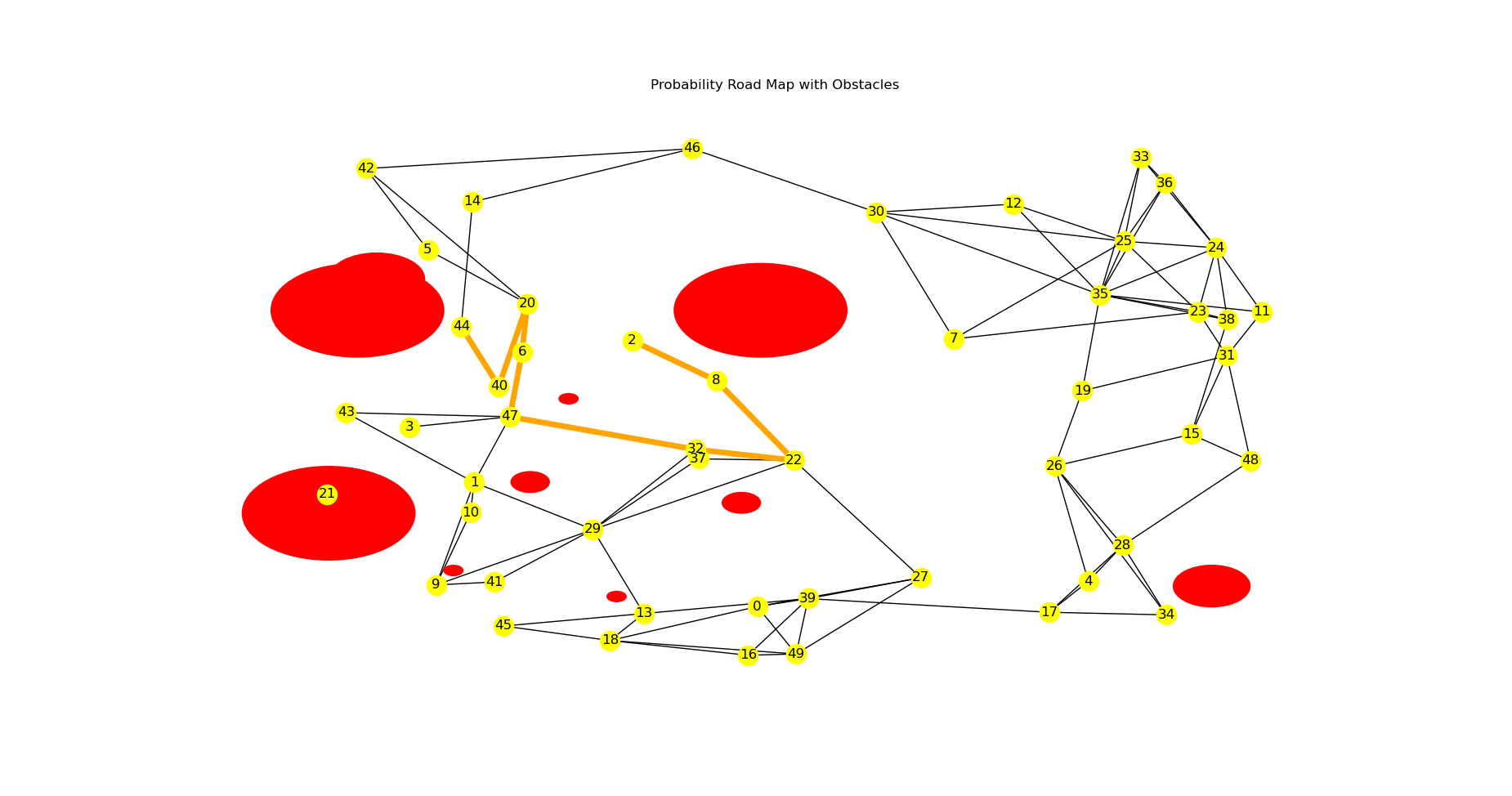
The image below shows a Probabilistic Roadmap with the shortest path (in orange) from node 44 to node 2 : [44, 40, 20, 6, 47, 32, 22, 8, 2]. The obstacles are shown in red and the nodes in yellow.

 

Algorithm Description

It consists of two phases

• CONSTRUCTION PHASE
• QUERY PHASE

Construction Phase

• Random Sampling: Random snapshots(samples) of different places that the robot could be in its environment.

• Checking for Free Space: Each snapshot is checked to see if it's a safe spot for the robot to be in (no obstacles).

• Connecting the Dots: For each safe spot, other nearby spots are checked to see if it can easily connect to without hitting any obstacles, typically either the k nearest neighbors or all neighbors less than some predetermined distance.

• Building a Road Map: This is done iteratively till enough snapshots and pathways are present that cover different ways the robot could move around and until the roadmap is dense enough. This collection of snapshots and connections becomes the "map" or "roadmap."

Query Phase

• Setting Start and Goal positions: The starting position and the destination position are marked on the map.
• Linking with best route: The positions are linked to the roadmap created and the best route is formed from start to end using a Dijkstra's shortest path query.

Rapidly-exploring Random Tree (RRT)

Clone into directory and Run using python3 rrt.py for RRT with obstacles and python3 rrt_without_obstacles.py for RRT without obstacles.

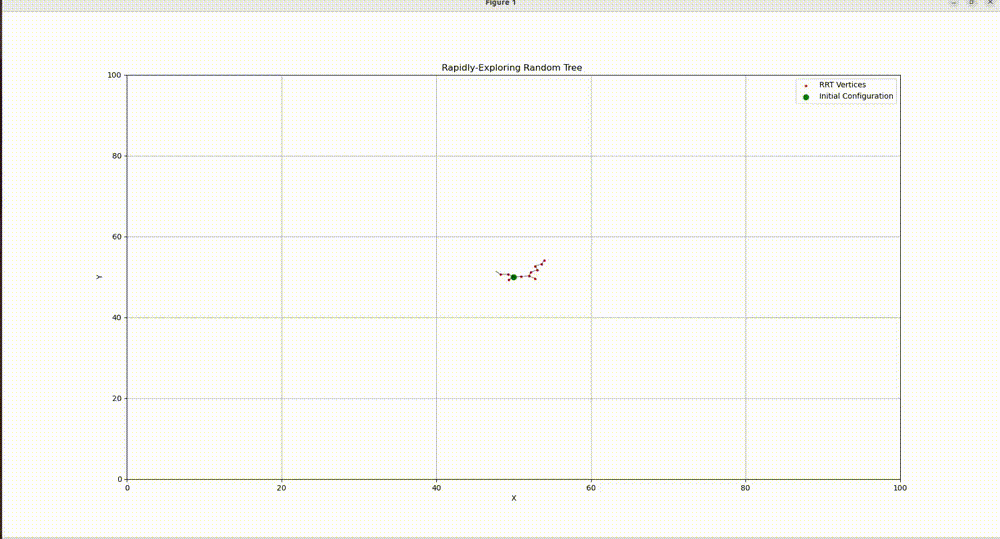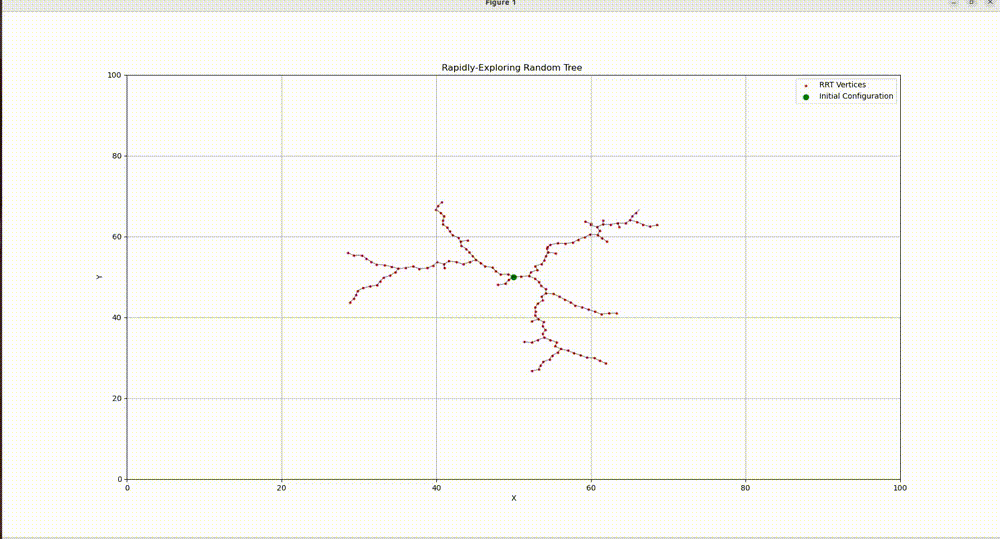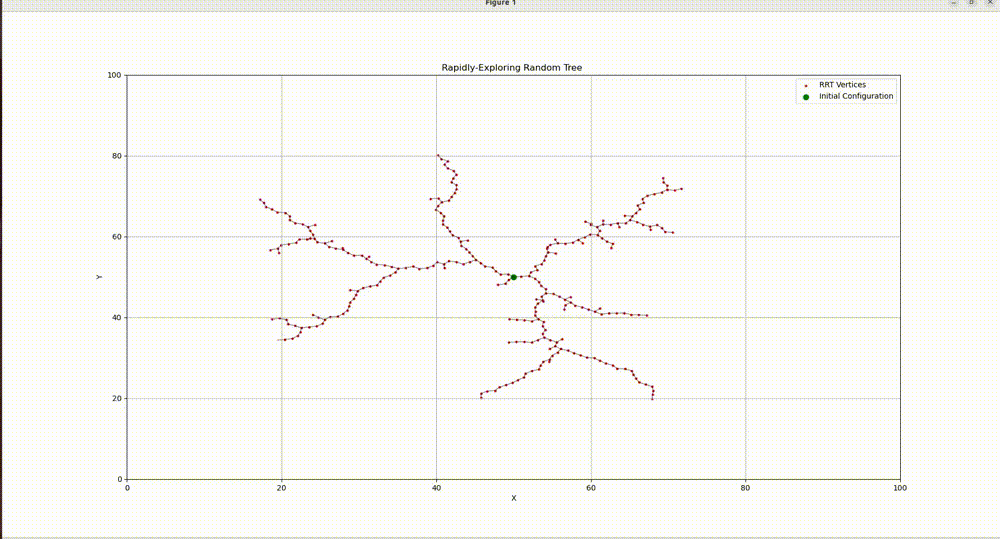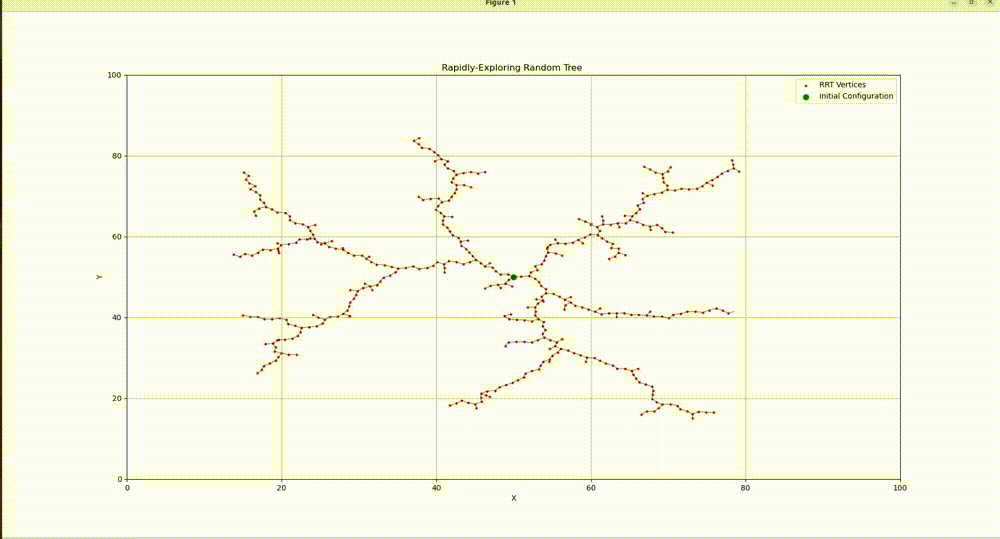
A Rapidly-Exploring Random Tree (RRT) is a fundamental path planning algorithm in robotics, first developed by Steven LaValle in 1998. An RRT consists of a set of vertices, which represent configurations in some domain D and edges, which connect two vertices. The algorithm randomly builds a tree in such a way that, as the number of vertices n increases to ∞, the vertices are uniformly distributed across the domain D⊂Rn.

RRT without obstacles - 1000 iterations

 

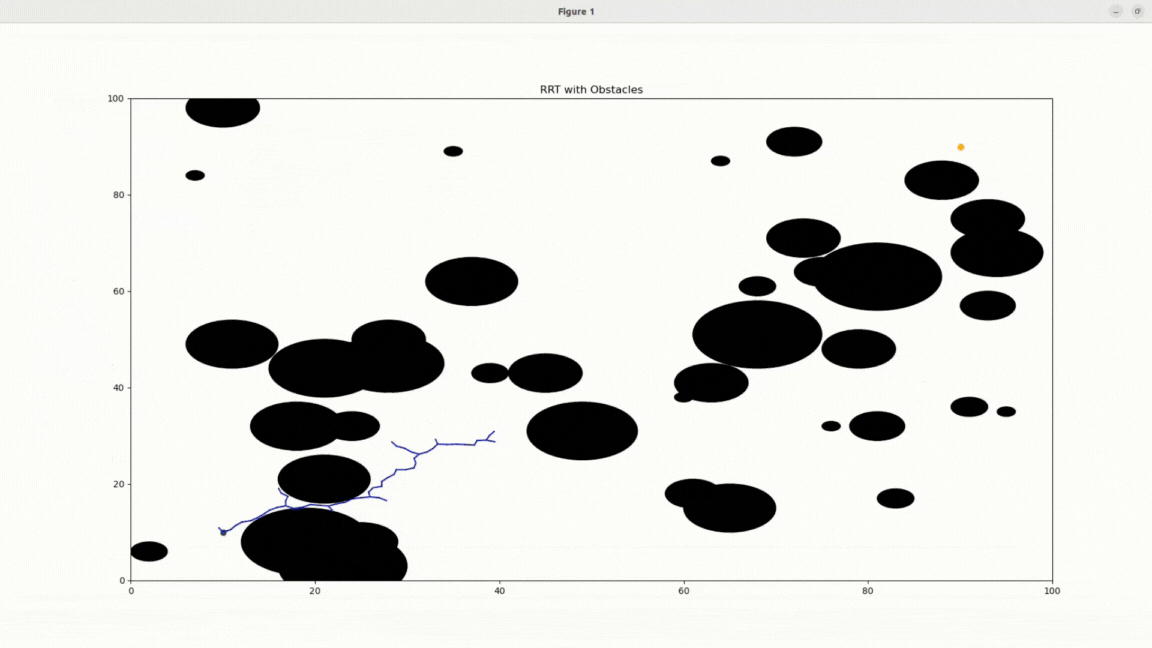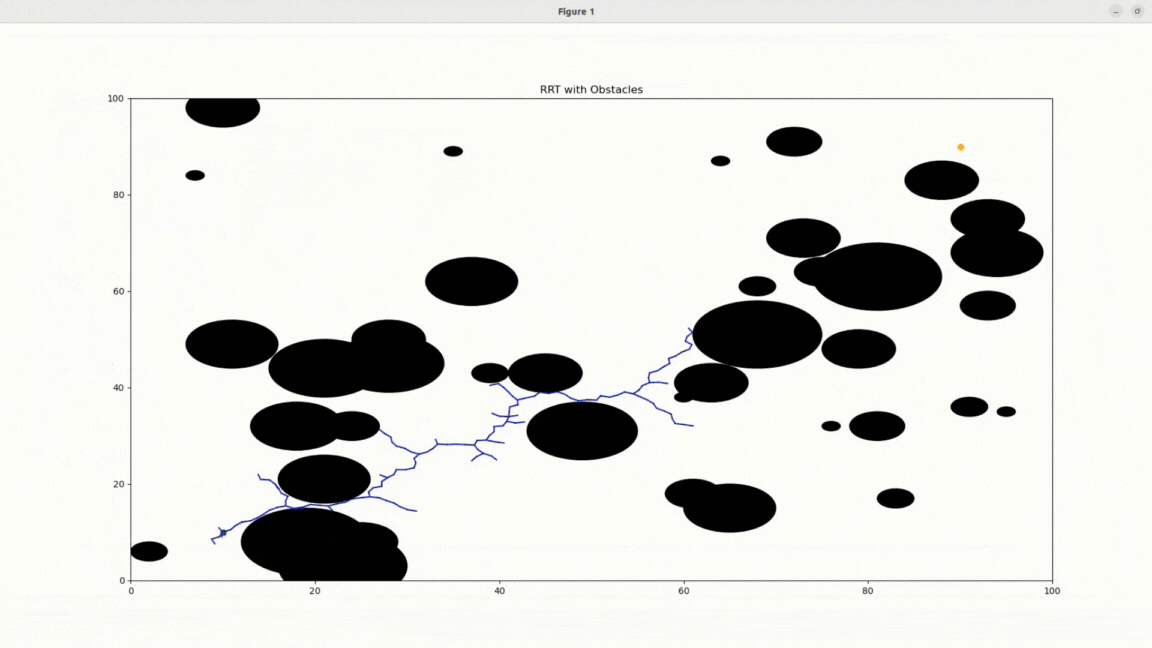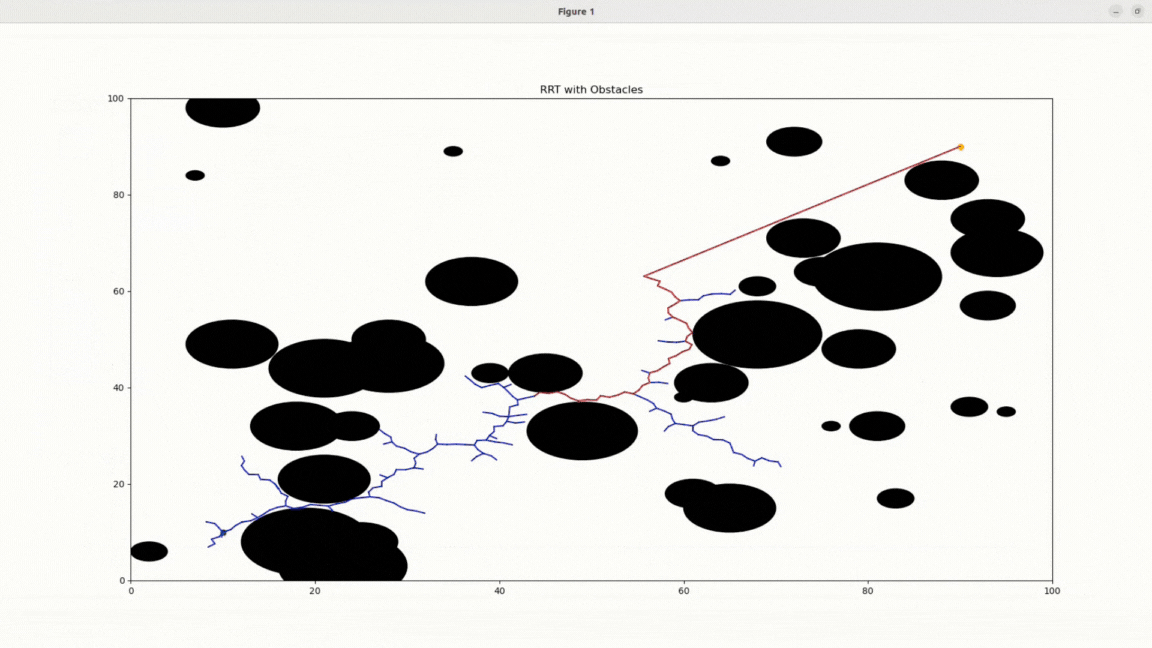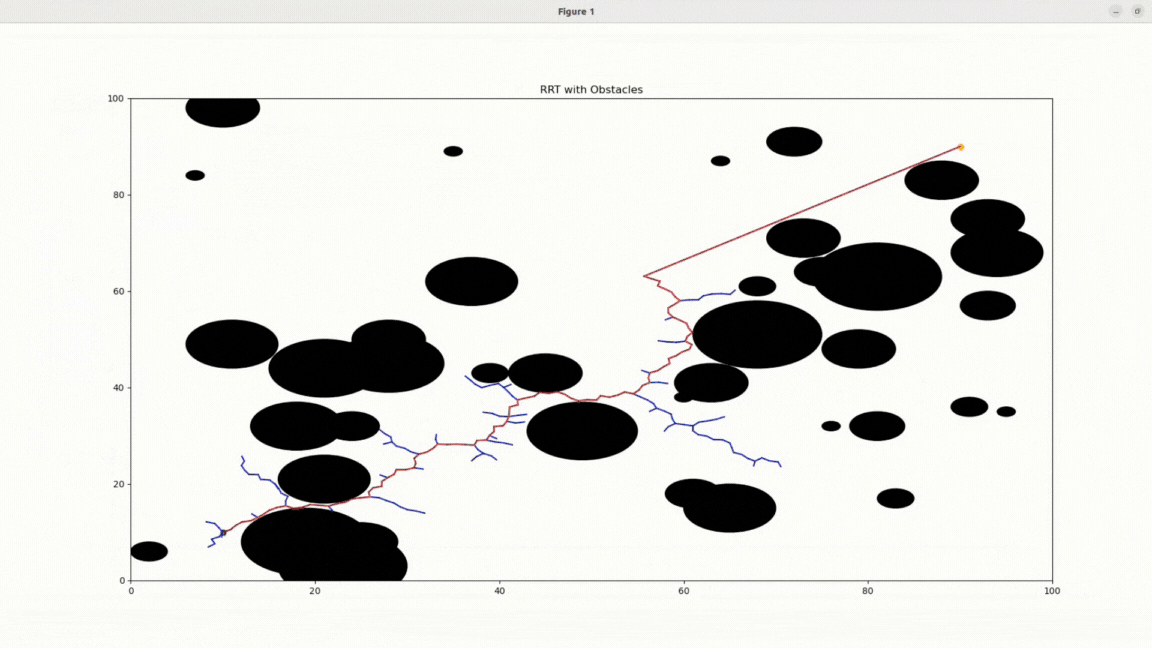
RRT with obstacles

 

Algorithm Description

RRT Algorithm

 

RANDOM_CONFIGURATION : Generates a random position in the domain.
NEAREST_VERTEX : finds the vertex in G that is closest to the given position, according to some metric (a measure of distance). We will use the Euclidean metric.
NEW_CONFIGURATION : generates a new configuration in the tree by moving some distance Δ from one vertex configuration towards another configuration.

Modification for RRT with obstacles

Collision Checking Steps

• Before Adding qnew to the Tree: Check if the path from qnear to qnew intersects with any obstacles. Collision occurs if the line between these vertices intersects any obstacle circles.

• After Adding a New Vertex: Check for a collision-free path from the new vertex to the goal. If a collision-free path exists, terminate the algorithm.

Path Finding Steps:

• Finding a Path to the Goal: Once a vertex in the tree connects to the goal state, a collision-free path from that vertex to the goal is sought.

• Backtracking for Path Reconstruction: When a path from a tree node to the goal state is found, traverse backward from the goal state through the connected nodes to reconstruct the complete path from the starting location.