[MRG] new K-means implementation for improved performances

[jeremiedbb]

This is work in progress toward an improved implementation of K-means, performance-wise. It's an attempt to implement some of the propositions in #10744.
Currently this is only done for the lloyd algorithm.
The main difference with the current implementation is running the steps of the algorithm over data chunks, allowing better cache optimization and parallelization.

Although this is still WIP and there's a lot more work to do, any comment is appreciated.

Currently there are 2 implementations of lloyd algorithm, triggered by the precompute_distances parameter. When False, the pairwise distances between the data points and the centers are computed in a cython loop, using level 1 BLAS functions. This is not efficient. When True, the pairwise distances are precomputed before the cython loop, using level 3 BLAS functions through numpy.dot. This is very efficient. However the obtained pairwise distances matrix can be quite large and does not fit in the cpu cache which may cause a big overhead.

The proposed implementation tries to solve both issues. The pairwise distance matrix is precomputed using level 3 BLAS functions, one data chunk at a time. This would result in simpler implementation: no need for 2 different implementations.
Also it may also allow a better parallelization, at the chunks loop level (although this need more test right now).

This first implementation shows improvement, on single thread, by a factor of 2 to 8 versus master (I'll post some benchmarks soon). However it is still slower than the intel implementation by a factor of 2, and I need to investigate further.

There is still a long todo list

• publish benchmarks on single and mutli thread.

• find good chunk size is important for the performances

• add sample weight

• support sparse

• clean now unnecessary code

• investigate the elkan algorithm

• investigate the centers initialization (kmeans++) (will do in separate PR)

Fixes #9943, fixes #10744

[jeremiedbb]

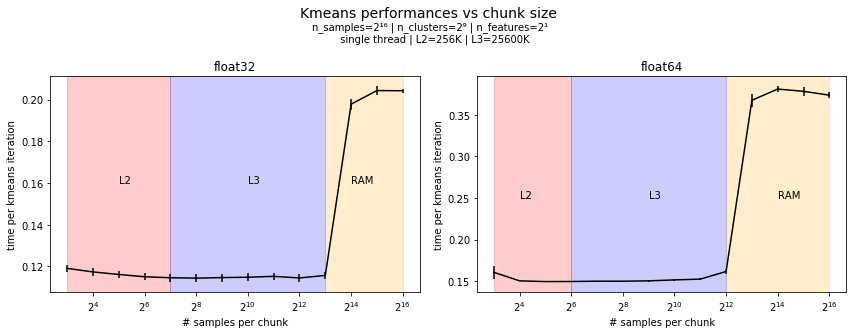
Here comes some benchmarks showing the importance of choosing the right chunk size. The following plot shows the time of a single kmeans iteration for several chunk sizes. The chunk size is the number of samples per chunk. This correspond to a memory allocation of size chunk_size x n_clusters for the pairwise distance matrix.

If the chunk size is too small (<2⁷ here) the overhead of -I guess- malloc/free is too high. Edit: after investigation, malloc/free are really fast compared to the computation time. It's more probably the fact that the flops are lower for smaller matrix multiplications.
If chunk_size < 2¹⁰, the pairwise distance matrix fits into the L2 cache and the performance is the best possible.
If chunk_size < 2¹⁹, the pairwise distance matrix no longer fits into the L2 cache but still fits into the L3 cache. The performance decreases a bit.
Beyond that, the pairwise distance matrix does not fit in the cache and performance decreases again.



Here are some more benchmarks showing that the gain of performance of fitting into L2 if often surpassed by the overhead (when n_clusters is too high then the chunk size has to be too small to fit into L2), and that the loss of performance of not fitting into L3 can be quite large.

Based on this, a very simple strategy can be used for choosing the chunk size, at least on single thread. We want to choose the smallest chunk size that implies no overhead. 2⁸ seems to be a good candidate.
The good news is that we don't have to check the machine specs to choose the chunk size. The benchmarks on the post below are made with this unique chunk size and gave the best results.

Note however that this is on single thread and that it will have to be adjusted for multi-threads. I'm running benchmarks for that and I'll put them here.

[jeremiedbb]

Here is a benchmark using chunks of 2⁸ samples, as explained above. It's a comparison between intel, master and this PR, of the time per iterations for different n_samples (from 2¹⁰ to 2¹⁷). This is also on single thread.

It's interesting to see the bump on the 'master' curve. It's due to the fact that the precomputed pairwise distance matrix does not fit in the cache when n_samples is too big, reducing the performances.

In terms of speedup, the above benchmark gives

I ran this kind of benchmark for many values of n_clusters (from 2³ to 2⁹) and n_features (from 2¹ to 2⁶) and they all look like this one. Overall, the ratio of 'master' and 'intel' is 4.3 on average, and the ratio of 'PR' and 'intel' is 1.7 on average.

[jnothman]

Nice work! though I've not yet looked at the code... All the CI say no, btw.

I would think cases with n_clusters < 2**3 are very common. Is there a good reason not to benchmark those smaller numbers?

[jeremiedbb]

All the CI say no, btw.

There are still a lot of holes in my code :) Especially I didn't implement the sparse case.

Is there a good reason not to benchmark those smaller numbers?

Absolutely not. I'll run them. Edit: results are quite similar. For instance the benchmark below is for 2 clusters in 2 dimensions.

And in term of speedup:

I also added the same benchmarks with data stored as np.float64.

[jeremiedbb]

Here is a benchmark showing the performance difference when using different compilers.

In all cases, it's compiled with -O3 flag only. It appears that intel compiler is able to perform more optimizations that gcc. Actually, it fills the gap between 'PR' and 'intel' in the previous benchmark.

[ogrisel]

Another benefit of this implementation is that the memory usage should be limited. In particular that should also probably fix #9943 (I have not checked).

[ogrisel]

The intel compiler is impressive. I wonder if we would observe similar results on the rest of the scikit-learn cython code base. If it's the case it's worth considering this as the compiler used to generate the scikit-learn wheels.

[ogrisel]

@jeremiedbb is your benchmark of compilers in #11950 (comment) running on a single thread?

The implementation of openmp in clang/llvm should be similar to the one in icc as it was contributed by intel.

[ogrisel]

@jeremiedbb BTW congrats on the quality of the reporting of your benchmarks and the analysis in terms of CPU cache size. This is really enlightening and appreciated.

[ogrisel]

Also note that when @jeremiedbb mentions the "intel implementation" of K-means, it's the one from the intel distribution of scikit-learn. In particular the K-means C++ implementation is provided by DAAL: https://github.com/intel/daal/tree/daal_2018_update3/algorithms/kernel/kmeans

[jeremiedbb]

is your benchmark of compilers in #11950 (comment) running on a single thread?

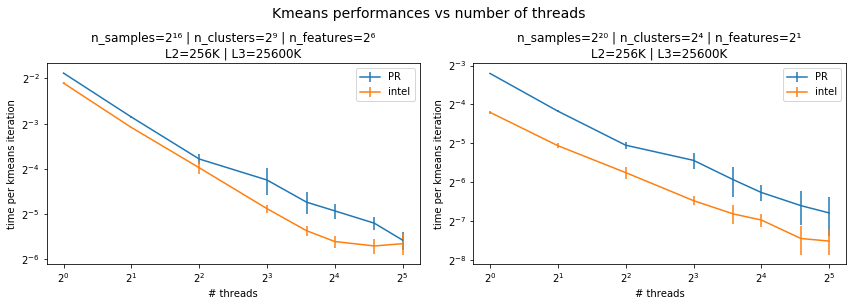
yes it's on single thread.

Here is a benchmark on how it behaves on multi-threads (for 2 problems with different number of clusters and features), compared to the intel implementation.

[ogrisel]

I have a hard time reading times in power of 2. Please use regular (decimal) tickers and a log scale in matplotlib instead.

The scalability looks good though :)

[ogrisel]

Also maybe use 10x the number of samples to get more interesting running times. We are really not interested in optimizing k-means in the subsecond regime :)

[jeremiedbb]

I have a hard time reading times in power of 2. Please use regular (decimal) tickers and a log scale in matplotlib instead.

I agree but for this benchmark, we are not interested in the absolute time. I put base 2 because I find it easier to see if time is divided by 2 when the number of threads is doubled

[jeremiedbb]

Quick note about numerical precision issues

K-means being based on euclidean metric, it's impacted by #9354. Although we don't use euclidean_distances, we use the same trick for a fast computation of the pairwise distances matrix.

However, the absolute values of the distances are irrelevant for this algorithm. What matters is their ordering. Therefore this numerical precision should have a minor effect on the clustering. I've made some tests and they seem to confirm that intuition. Below is an example of the clustering using the fast and the exact distance computation (data stored on float32). For this example, the final inertiae differ by about 1%.

I made other tests with various kinds of clusters, scales, numbers, dimensions, and I haven't found a situation where this numerical precision issue disturbs the behavior of the algorithm. Therefore I suggest that we keep this fast method for computing the pairwise distances in K-means.

There is still a visible effect. Although the clustering is fine, the absolute distances might not be and the inertia could be wrongly evaluated. This is because the inertia is computed incrementally by the distances of each sample to it's closest center using the fast method. The solution is to compute the inertia using the stable method, once the labels are updated: inertia = ((X - centers[labels])**2).sum()

[rth]

Very nice work on this in general!

However, the absolute values of the distances are irrelevant for this algorithm. What matters is their ordering.

Well the thing is as illustrated in #9354 (comment) for vectors closer than some threshold, the distance may be 0.0 while it shouldn't be, and then your ordering will also not be correct. But I agree that as far as this PR goes, one might as well ignore it, it's a more general issue...

[jeremiedbb]

Yes but for a sample to be wrongly labeled due to that issue, it means that the distance between this sample and say 2 centers are very close. Hence you can't say that this sample should belong to one cluster or the other. Moreover, inertia should be almost the same in both case, and you end up in 2 different local minima, with approx the same score.

[amueller]

Can I ask how much time the total time until some sort of convergence is on these benchmarks?
Honestly I'm not very excited by a speedup factor of 5 going from 0.005 seconds to 0.001 seconds. There seems very few use cases where that makes a difference, right?

[jeremiedbb]

The y axis on my plots shows the time for a single iteration of k-means. You get the same speed up factor for the full KMeans.fit(), for any problem size.

Let's say for example you have 100000 samples, 100 clusters, 10 features. One iteration takes ~25ms. If you have around 100 iterations until convergence (max_iter default is 300), the fit takes 2.5s, vs 5s+ before.

Now if you have 10x more samples it's 25s vs 50s+.
And if you put n_init=10, it's 250s vs 500s+.

Moreover, the parallelization is now at the loop over samples level, which allows the possibility to use all cores. With the current parallelization being at the init level (which default is 10), you can only use n_init cores.

For a concrete example, let's take the example of color quantization in sklearn, but fitting the whole image, not a subsample. On master, it takes 164s, vs 27s with this implementation (on single thread).

[amueller]

Thanks for the explanation.

[jeremiedbb]

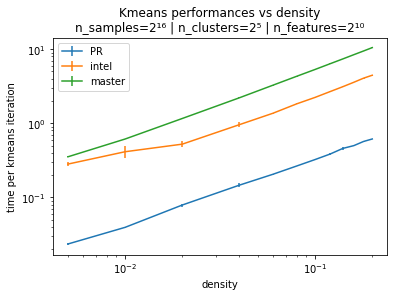
Below are some benchmarks for the sparse case.

This one is a benchmark of the performances versus the number of features, for 8 clusters on the left and 128 on the right. This is on single thread.

and in terms of speedup

Here is a benchmark of the performances versus the density of the data sparse matrix.

and in terms of speedup

[ogrisel]

One way to explain the difference with intel, is that intel is using sparse matrix matrix multiplications from MKL to compute the distance while the Cython code of @jeremiedbb is computing the distances naively but leveraging the sparsity. Apparently for this problem, not using matrix matrix multiplications is the best strategy.

[jeremiedbb]

Here is a benchmark for multithread scalability with sparse data.

I'm not sure why the performances decrease at 32 threads. It might be that the gil acquisition for the reduction begins to cause a noticeable overhead, but it's more a guess than an explanation.

Edit: I don't know what is the reason of the perf decrease in the previous benchmark, but it might be related to some unknown about the machine I'm running them on (virtual cpus). Because I ran it again and the results are as expected. I would expect this kind of difference if one machine use hyperthreading (i.e. 16 actually physical cores) and the other has 32 physical cores.

Anyway, scalability looks good. Maybe sometimes not smart to use all available cores.

[jeremiedbb]

I have a more formal justification about why numerical precision issues from euclidean distances don't impact k-means, or at least this new implementation.

First, let's see where this issue comes from. Let x be a sample point and c be a center. Let's suppose that x and c are close (otherwise, x would be eventually assigned to a closer center and bad computation of the distance between x and c would be irrelevant), that is
c = x + eps where ||eps|| << ||x||
Thus

d(x,c)² = d(x,x+eps)² = ||x - (x + eps)||² 
                      = ||x||² + ||x + eps||² - 2x.(x + eps)
                      = ||x||² + ||x||² + ||eps||² + 2x.eps - 2||x||² - 2x.eps
                      = ||eps||²

Then, due to precision limit, an error of order ||eps||² results in an important relative error (||eps|| is not small vs 1, it's small vs ||x||).

The thing which save us here is that we do not compute all the terms in the distance expansion. When we need to find the closest center for a given sample x, i.e.

min_c(d(x,c)) = min_c||x-c||² = min_c(||x||² + ||c||² - 2x.c)

we don't need to compute ||x||² since it does not depend on c. Therefore, when c = x + eps, we only compute

||c||² - 2x.c = ||x + eps||² - 2x.(x + eps)
              = ||x||² + ||eps||² + 2x.eps - 2||x||² - 2x.eps
              = -||x||² + ||eps||²

Here an error of order ||eps||² results in a small relative error.

[jeremiedbb]

@NicolasHug I thought I could delete comments that were duplicated as answers in previous review and comments in new review but in tunred out that it deleted both :/
These were comments that I answered but now the discussion is a bit weird since a comment is missing. Sorry about that.

[NicolasHug]

LGTM

Thnanks for the great work @jeremiedbb

[jeremiedbb]

@NicolasHug I think I addressed most of your comments (still remains the testing of some private utility functions). I marked them as resolved when I applied your comments as is, and left open the others. You can mark those as resolved if you are satisfied by my answers.

[NicolasHug]

I tried to resolve my comments yesterday but github was giving me errors so I'll leave it like that, they're all minor or addressed anyway.

I haven't merged because I wasn't quite sure whether you wanted to push a few last touches. Feel free to self merge!

[ogrisel]

I did another pass after @NicolasHug's review comments have been addressed. It still LGTM. Great work, merging!

[trevorboydsmith]

i noticed in the scikit-learn v0.23 release notes that the KMeans input parameter for n_jobs is deprecated and will be removed in v0.25. all that is mentioned is that the parallelization is being done differently now (previously it was done via joblib and now it is done via openmp).

i use the kmeans and i also use the n_jobs param and it does speed things up.

my question is. does the new v0.25 version without n_jobs still parallelize yes or no?

is the parallelize just automatic (no need for user because it knows what is best)?

[jeremiedbb]

i use the kmeans and i also use the n_jobs param and it does speed things up.

n_jobs can still be used in 0.23 and 0.24. However, if you leave the default value, kmeans will now use as many cores as possible.

my question is. does the new v0.25 version without n_jobs still parallelize yes or no?

from 0.25, it will still use all cores. There are tools to modify the number of core used described in the user guide, such as the OMP_NUM_THREADS env var.

[trevorboydsmith]

thanks for the speedy reply and the clarification. glad to hear the parallel processing is still there and just changing the implementation of how the parallelization is done.

for my own edification: if you are parallelizing at the openmp/c++ level i guess your code is already c++ and therefore better to do parallel processing at c++/low-level as opposed to the old way of parallelizing at the higher-level python level with joblib?

[jeremiedbb]

here's a blog post I wrote about that which describes the new optimizations and the change in the parallel scheme.