AI-Negotiator

A negotiating agent written in Python

Background

Each negotiation will be over a set of items that have a utility value specific for each negotiator (not necessarily the same). The negotiation structure will consist of alternating offers with a finite turn limit.

Rules: Each offer will be the set of items a negotiator wishes to take for itself. Both agents will receive a substantial negative reward if no agreement is made.

Goal: Within finite turns, get higher reward.

Language: Python

Negotiating Strategy

After a brief analysis of how to get maximum reward, or our baseline limit, we found the following strategies:

*Note: Starting first will be able to make the final offer, starting second will be able to decide whether to accept opponent's final offer

1. 2/3 of total reward, accept! Since opponent’s total utility and preferences for items are different than ours. As soon as we receive 2/3 of our total reward, we accept the offer.

2. 1/3 of total reward, baseline. If I start second, I can decide whether to accept opponent's final offer. Accept any offer more than 1/3 of my total utility

3. Keep track of opponent's favourite list. Keep track of how many times each item the opponent has requested.

Pseudo Code for Decision Making

# initialize a global variable to store the maxTurns
maxTurns = 0
# declare a global dict to keep track for opponent's moves
oppo_dict = {}

def make_offer(self, offer):
     update the current turn
     update opponent offer in oppo_dict

     if going first, offer all positive util items

     if last turn:
        if last chance to accept offer:
          accept any offer more than 1/3 of my total utility OR just reject the offer and take penalty             
     
        else you are to give the final offer:
       	  add items that opponent never offered to my wanted list
       	  if less than 2/3 amount achieved
       	    add the opponent least wanted one until we reach 2/3
     
     Negotiating moves:
        if offer is not None:
      	  if more than 2/3 will receive, accept, negotiation completed!
      		else
       	  	instantiate our offer to whatever left
            while our offer < 2/3 of total utility
          	  add max worth item in opponent offer

Code Example

Decision process for final offer, including giving, accepting, and rejecting

        # to see if it is the last turn, and accept whatever offer
        if currentTurn is maxTurns:
            if currentTurn > ky2cg.getTurns(self):
                # then you are to accept the final offer

                self.offer = offer
                self.offer = BaseNegotiator.set_diff(self)

                if (self.utility() >= (self.totalUtility() / 3)):
                    return self.offer

                else:
                    self.offer = BaseNegotiator.set_diff(self)
                    # print "You bad!!! I'd rather get negative leward!!!!"
                    return self.offer
            else:
                # then you are to give the final offer
                total = 0
                ourOffer = []
                # look at the nonoffered items first
                ordering = self.preferences
                for item in ordering.keys():
                    if not oppo_dict:
                        break
                    if (item not in oppo_dict and ordering.get(item) >= 0):
                        ourOffer = ourOffer + [item]
                        total += ordering.get(item)
                        if (total >= (2 / 3 * self.totalUtility())):
                            self.offer = ourOffer
                            return self.offer

            while total < (2 / 3 * self.totalUtility()):
                min = min(oppo_dict, key=oppo_dict.get)
                ourOffer = ourOffer + min
                total += oppo_dict.get(min)
                del oppo_dict[min]
            self.offer = ourOffer
            return self.offer

Testing

total-random negotiator: To test the efficiency of our negotiating algorithm we created total-random negotiator. The total-random negotiator utilize extremely simple and random algorithm, randomly compile an offer that is greater than 2/3 of total utility if it goes first. When it is given an offer, it will probabilistically accept the offer or reject the offer by offering back the same offer. When it is the last turn, the algorithm will accept any offer so that a deal could be made.

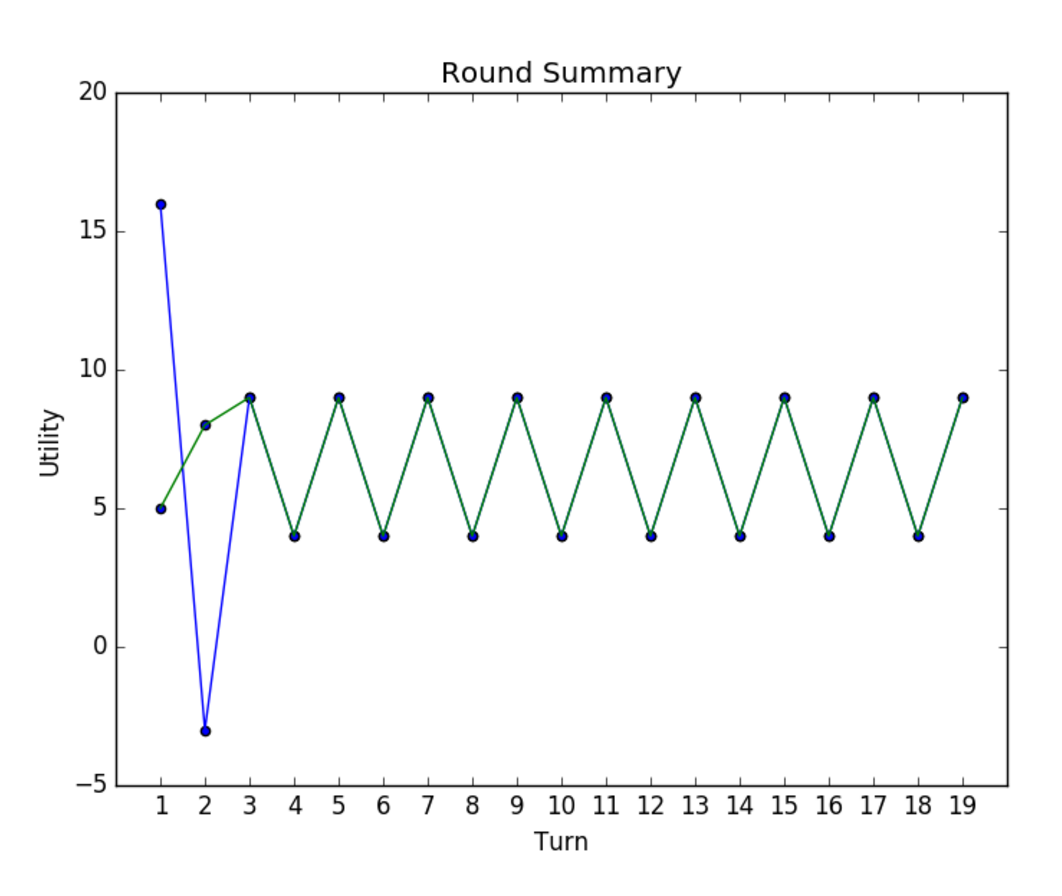
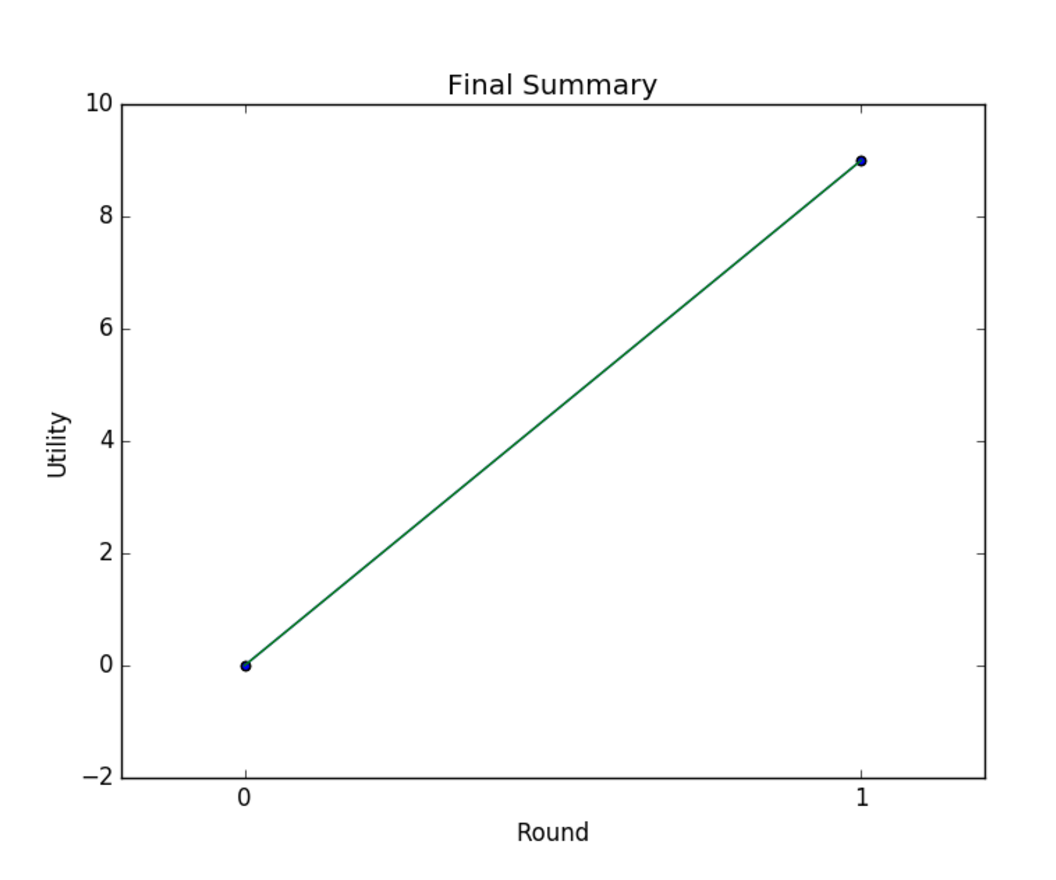
When we tested our code against this total-random negotiator we realized this will end up, in most cases, deterministic, meaning the utility received by both parties are the same over every iteration. See results below (total-random utility: 9, main algorithm: 9):

List of items and their rewards:

Round summary and final summary:

Analysis

One key insight we had was the possibility of opponent using an extremist algorithm that pushes very aggressively for a high utility value for them. We had to account for that by building in different thresholds at different stages of the negotiation in which we will accept an offer. Our original algorithm also did not account for opponent’s actions, other than the offer they present. By developing the functionality that keep track of what the opponent has offered in the past, we are able to better adjust our strategy in late-game scenarios.

The testing results we saw throughout this project demonstrated that this algorithm can become very deterministic, depending upon the opponent’s strategy. This is not alike what a human negotiator would do, where backtracking, price-raising, etc. can be used in response to what an opponent does.

Our implementation is not an overly aggressive one, in that it does not push the negotiation to the brink in order to maximize our gain. We believe this algorithm that aims for a fair distribution that can benefit both parties can maximize our opportunities in achieving a high overall utility after many rounds of negotiations, facing different negotiators.