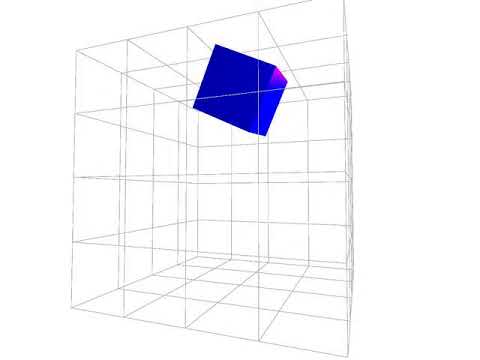
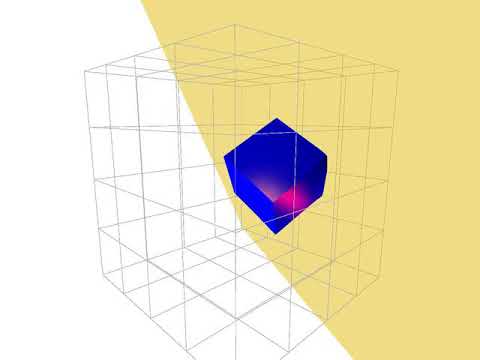
It's a physically based simulation for a deformable jello cube.
- Type
maketo complete - Run with ```./jello some_world_file.w
- During simulation press v to turn on full rendering of the cube. Press
sto show/hide structural springs. Pressbto show/hide bend springs. Presshto show/hide shear springs. Press 'i' to enter interactive mode. Further instructions for interactive mode are illustrated in terminal while running the program. - You can also use createWorld routine to create your own world file.
- Simulated the jello cube in a physics realistic way
- Added top and bottom walls to make the scene an enclosed world
- Changed lighting and material style to be more cyberpunk
- Implemented functionality that allow users to use arrow keys to move the scene. Left and right keys are for horizontally translate camera along a curve. Up and down are for vertically translate the camera along a curve. Press 'e' to reset.
- Created multiple different world files with non-homogeneous (in space) force fields
Since force fields are just vector fields; and since vector fields can be defined
as functions that maps R^3 to R^3, to create force fields, we just need to map
all positions of points in the force field (i.e. (x,y,z) indecies) to some functions
about (x,y,z).
Here are force fields I created:
-
strongerRotate.x It is the same motion with rotate.x but forces are stronger. Mapping function: F(x,y,z)=(-y/10)i+(x/10)j+0k
-
pushToCenter.w This world file's force field has all forces pointing to origin (0,0,0). Hence, the cube will be eventurally pushed around the center of the world. Mapping function: f(x,y,z) = (2(-x)/(x^2+y^2+z^2))i +(2(-y)/(x^2+y^2+z^2))j +(2(-z)/(x^2+y^2+z^2))k
-
accelerate.w This world file's force field have smaller forces at +y direction but larger forces at -y direction. As a result, putting the cube on furtherest +y direction creates an effect of acceleration. The cube first moves slowly then suddenly gets crazy, rotating and rushing to -y wall. Mapping function: f(x,y,z) = (-sin(x)/(x^2+y^2+z^2))i +(logb(y)/(x^2+y^2+z^2))j + 0k
-
- Implemented inclined plane collision:
- Implemented functionality to detect collision against the inclined plane on either sides.
- Implemented functionality to display inclined plane as a square by finding binormal vectors to the plane defined by normal [a,b,c] and linearly combine the binormal vectors to form four corners of the square.
- Use OpenGL blending function to make the inclined plane to be half transparent so that it is prettier
- Implemented mouse drag user interaction for pushing the cube
- With a .w file open, you can press 'i' to turn on interaction mode.
- Dragging up and down moves the cube up or down.
- Dragging left and right moves the cube on x-y plane. For this, four modes of directions of movement are implement. You can press 'i' to switch modes. 1> Mode 1 - Diagonal Drag of (-x,y,z) to (x,-y,z) 2> Mode 2 - Diagonal Drag of (x,y,z) to (-x,-y,z) 3> Mode 3 - Drag between Left and Right Walls 4> Mode 4 - Drag between Front and Back Walls
- Amount of forces added to the cube is determine by how far you have moved the mouse. The equation I used for calculating magnitude give a normalized force point is: sqrt(x-movement^2, y-movement^2)/20 * (1/dt)/1000 the dividing 20 part is for preventing force is too large that will destroy the cube's structure. And the (1/dt)/1000 magnify the force for smaller timesteps. For 0.001 timestep, (1/0.001)/1000=1. But for smaller timestep, the value of this part will always be greater than 1. This is a consideration that worlds with smaller timestep runs slow, so dragging effect is less obvious; magnifying force solves this problem.
- You will also see explanations about how to interact with the cube in the console ;)
- Animation 1 is an execution with pushToCenter.w. Some additional forces from user push on (x,y) to (-x,-y) and plane and +z direction are added to create some dynamics. You can also observe the force field tries to move the cube around the center of the world.
- Animation 2 is an execution with accelerate.w. It is mainly to show collisions with walls and the inclined plane. You can also observe the cube accelerates due to the forces given by force field.