-
Notifications
You must be signed in to change notification settings - Fork 15
Radix Sort #46
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Merged
Merged
Radix Sort #46
Changes from all commits
Commits
Show all changes
9 commits
Select commit
Hold shift + click to select a range
4a6d37c
docs: readme for radix sort
yeoshuheng 694b75e
docs: update readme for radix sort
yeoshuheng 3474233
feat: junit test for radixsort
yeoshuheng 6d8381b
fix: checkstyle errors
yeoshuheng 86825a6
docs: updated readme to talk about number systems
yeoshuheng b6add13
docs: added comments on O(N) implementation trick
yeoshuheng 3b3aacd
docs: added comments on bit masking
yeoshuheng c2b1bb9
docs: updated readme
yeoshuheng 587a40c
docs: updated read me
yeoshuheng File filter
Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,65 @@ | ||
| # Radix Sort | ||
|
|
||
| ## Background | ||
|
|
||
| Radix Sort is a non-comparison based, stable sorting algorithm with a counting sort subroutine. | ||
|
|
||
| Radix Sort continuously sorts based on the least-significant segment of a element | ||
yeoshuheng marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| to the most-significant value of a element. | ||
|
|
||
| The definition of a 'segment' is user defined and defers from implementation to implementation. | ||
| Within our implementation, we define each segment as a bit chunk. | ||
|
|
||
| For example, if we aim to sort integers, we can sort each element | ||
| from the least to most significant digit, with the digits being our 'segments'. | ||
|
|
||
| Within our implementation, we take the binary representation of the elements and | ||
| partition it into 8-bit segments, a integer is represented in 32 bits, | ||
| this gives us 4 total segments to sort through. | ||
|
|
||
| Note that the binary representation is weighted positional, | ||
| where each bit's value is dependent on its overall position | ||
| within the representation (the n-th bit from the right represents *2^n*), | ||
| hence we can actually increase / decrease the number segments we wish to conduct a split from. | ||
|
|
||
| 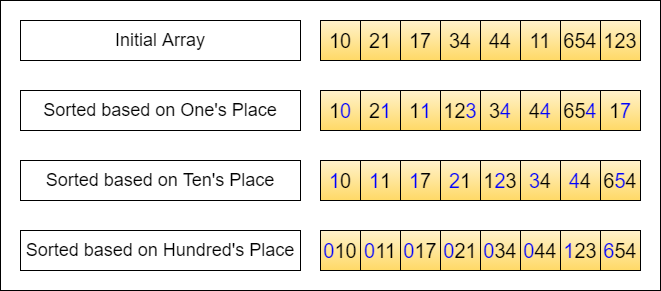 | ||
|
|
||
| We place each element into a queue based on the number of possible segments that could be generated. | ||
| Suppose the values of our segments are in base-10, (limited to a value within range *[0, 9]*), | ||
| we get 10 queues. We can also see that radix sort is stable since | ||
| they are enqueued in a manner where the first observed element remains at the head of the queue | ||
|
|
||
| *Source: Level Up Coding* | ||
|
|
||
| ### Implementation Invariant | ||
| At the start of the *i-th* segment we are sorting on, the array has already been sorted on the | ||
| previous *(i - 1)-th* segments. | ||
|
|
||
| ### Common Misconceptions | ||
|
|
||
| While Radix Sort is non-comparison based, | ||
| the that total ordering of elements is still required. | ||
| This total ordering is needed because once we assigned a element to a order based on a segment, | ||
| the order *cannot* change unless deemed by a segment with a higher significance. | ||
| Hence, a stable sort is required to maintain the order as | ||
| the sorting is done with respect to each of the segments. | ||
|
|
||
| ## Complexity Analysis | ||
yeoshuheng marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| **Time**: | ||
| Let *b* be the length of a single element we are sorting and *r* is the amount of bit-string | ||
| we plan to break each element into. | ||
| (Essentially, *b/r* represents the number of segments we | ||
| sort on and hence the number of passes we do during our sort). | ||
|
|
||
| Note that we derive *(2^r + n)* from the counting sort subroutine, | ||
| since we have *2^r* represents the range since we have *r* bits. | ||
|
|
||
| We get a general time complexity of *O((b/r) * (2^r + n))* | ||
|
|
||
| **Space**: *O(n + 2^r)* | ||
|
|
||
| ## Notes | ||
| - Radix sort's time complexity is dependent on the maximum number of digits in each element, | ||
| hence it is ideal to use it on integers with a large range and with little digits. | ||
| - This could mean that Radix Sort might end up performing worst on small sets of data | ||
| if any one given element has a in-proportionate amount of digits. | ||
106 changes: 63 additions & 43 deletions
106
src/main/java/algorithms/sorting/radixSort/RadixSort.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -1,53 +1,73 @@ | ||
| package algorithms.sorting.radixSort; | ||
|
|
||
| /** | ||
| * Implementation of Radix sort. | ||
| * O((b/r)*(N + 2^r)) | ||
| * where N is the number of integers, | ||
| * b is the total number of bits (32 bits for int), | ||
| * and r is the number of bits for each segment. | ||
| * Space: O(N) auxiliary space. | ||
| */ | ||
| * This class implements a Radix Sort Algorithm. | ||
| */ | ||
| public class RadixSort { | ||
| private static final int NUM_BITS = 8; | ||
| private static final int NUM_SEGMENTS = 4; | ||
|
|
||
| private static int getSegmentMasked(int num, int segment) { | ||
| int mask = ((1 << NUM_BITS) - 1) << (segment * NUM_BITS); | ||
| return (num & mask) >> (segment * NUM_BITS); | ||
| } | ||
| private static final int NUM_BITS = 8; | ||
| private static final int NUM_SEGMENTS = 4; | ||
|
|
||
| private static void radixSort(int[] arr, int[] sorted) { | ||
| // sort the N numbers by segments, starting from left-most segment | ||
| for (int i = 0; i < NUM_SEGMENTS; i++) { | ||
| int[] freqMap = new int[1 << NUM_BITS]; // at most this number of elements | ||
| /** | ||
| * Creates masking on the segment to obtain the value of the digit. | ||
| * | ||
| * @param num The number. | ||
| * @param segment The segment we are interested in. | ||
| * | ||
| * @return The value of the digit in the number at the given segment. | ||
| */ | ||
| private static int getSegmentMasked(int num, int segment) { | ||
| // Bit masking here to extract each segment from the integer. | ||
| int mask = ((1 << NUM_BITS) - 1) << (segment * NUM_BITS); | ||
| return (num & mask) >> (segment * NUM_BITS); | ||
| } | ||
|
|
||
| // count each element | ||
| for (int num : arr) { | ||
| freqMap[getSegmentMasked(num, i)]++; | ||
| } | ||
| // get prefix sum | ||
| for (int j = 1; j < freqMap.length; j++) { | ||
| freqMap[j] += freqMap[j-1]; | ||
| } | ||
| // place each number in its correct sorted position up until the given segment | ||
| for (int k = arr.length-1; k >= 0; k--) { | ||
| int curr = arr[k]; | ||
| int id = getSegmentMasked(curr, i); | ||
| sorted[freqMap[id] - 1] = curr; | ||
| freqMap[id]--; | ||
| } | ||
| // we do a swap so that our results above for this segment is saved and passed as input to the next segment | ||
| int[] tmp = arr; | ||
| arr = sorted; | ||
| sorted = tmp; | ||
| } | ||
| sorted = arr; | ||
| } | ||
| /** | ||
| * Radix sorts a given input array and updates the output array in-place. | ||
| * | ||
| * @param arr original input array. | ||
| * @param sorted output array. | ||
| */ | ||
| private static void radixSort(int[] arr, int[] sorted) { | ||
| // sort the N numbers by segments, starting from left-most segment | ||
yeoshuheng marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| for (int i = 0; i < NUM_SEGMENTS; i++) { | ||
| int[] freqMap = new int[1 << NUM_BITS]; // at most this number of elements | ||
|
|
||
| public static void radixSort(int[] arr) { | ||
| int[] sorted = new int[arr.length]; | ||
| radixSort(arr, sorted); | ||
| arr = sorted; // swap back lol | ||
| // count each element | ||
| for (int num : arr) { | ||
| freqMap[getSegmentMasked(num, i)]++; | ||
| } | ||
| // get prefix sum | ||
| for (int j = 1; j < freqMap.length; j++) { | ||
| freqMap[j] += freqMap[j - 1]; | ||
| } | ||
| // place each number in its correct sorted position up until the given segment | ||
| for (int k = arr.length - 1; k >= 0; k--) { | ||
| int curr = arr[k]; | ||
| int id = getSegmentMasked(curr, i); | ||
| sorted[freqMap[id] - 1] = curr; | ||
| freqMap[id]--; | ||
| } | ||
| // We do a swap so that our results above for this segment is | ||
| // saved and passed as input to the next segment. | ||
| // By doing this we no longer need to create a new array | ||
| // every time we shift to a new segment to sort. | ||
| // We can constantly reuse the array, allowing us to only use O(n) space. | ||
| int[] tmp = arr; | ||
yeoshuheng marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| arr = sorted; | ||
| sorted = tmp; | ||
| } | ||
| sorted = arr; | ||
| } | ||
|
|
||
| /** | ||
| * Calls radix sort inplace on a given array. | ||
| * | ||
| * @param arr The array to be sorted. | ||
| */ | ||
| public static void radixSort(int[] arr) { | ||
| int[] sorted = new int[arr.length]; | ||
| radixSort(arr, sorted); | ||
| arr = sorted; // swap back lol | ||
| } | ||
| } | ||
39 changes: 39 additions & 0 deletions
39
src/test/java/algorithms/sorting/radixSort/RadixSortTest.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,39 @@ | ||
| package algorithms.sorting.radixSort; | ||
|
|
||
| import static org.junit.Assert.assertArrayEquals; | ||
|
|
||
| import java.util.Arrays; | ||
| import org.junit.Test; | ||
|
|
||
| public class RadixSortTest { | ||
| @Test | ||
| public void test_radixSort_shouldReturnSortedArray() { | ||
| int[] firstArray = new int[] {2, 3, 4, 1, 2, 5, 6, 7, 10, 15, 20, 13, 15, 1, 2, | ||
| 15, 12, 20, 21, 120, 11, 5, 7, 85, 30}; | ||
| int[] firstResult = Arrays.copyOf(firstArray, firstArray.length); | ||
| RadixSort.radixSort(firstResult); | ||
|
|
||
| int[] secondArray = new int[] {9, 1, 2, 8, 7, 3, 4, 6, 5, 5, 9, 8, 7, 6, 5, 4, | ||
| 3, 2, 1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; | ||
| int[] secondResult = Arrays.copyOf(secondArray, secondArray.length); | ||
| RadixSort.radixSort(secondResult); | ||
|
|
||
| int[] thirdArray = new int[] {}; | ||
| int[] thirdResult = Arrays.copyOf(thirdArray, thirdArray.length); | ||
| RadixSort.radixSort(thirdResult); | ||
|
|
||
| int[] fourthArray = new int[] {1}; | ||
| int[] fourthResult = Arrays.copyOf(fourthArray, fourthArray.length); | ||
| RadixSort.radixSort(fourthResult); | ||
|
|
||
| Arrays.sort(firstArray); | ||
| Arrays.sort(secondArray); | ||
| Arrays.sort(thirdArray); | ||
| Arrays.sort(fourthArray); | ||
|
|
||
| assertArrayEquals(firstResult, firstArray); | ||
| assertArrayEquals(secondResult, secondArray); | ||
| assertArrayEquals(thirdResult, thirdArray); | ||
| assertArrayEquals(fourthResult, fourthArray); | ||
| } | ||
| } |
Add this suggestion to a batch that can be applied as a single commit.
This suggestion is invalid because no changes were made to the code.
Suggestions cannot be applied while the pull request is closed.
Suggestions cannot be applied while viewing a subset of changes.
Only one suggestion per line can be applied in a batch.
Add this suggestion to a batch that can be applied as a single commit.
Applying suggestions on deleted lines is not supported.
You must change the existing code in this line in order to create a valid suggestion.
Outdated suggestions cannot be applied.
This suggestion has been applied or marked resolved.
Suggestions cannot be applied from pending reviews.
Suggestions cannot be applied on multi-line comments.
Suggestions cannot be applied while the pull request is queued to merge.
Suggestion cannot be applied right now. Please check back later.
Uh oh!
There was an error while loading. Please reload this page.