Implementasi
Implementasi adalah sebuah tindakan atau proses gagasan yang sudah disusun dengan cermat dan detail. Implementasi ini umumnya tuntas sesudah di anggap permanen.
- The Millennium Prize Problems - Pdf (4.8MB)
- Online Books: Clay Mathematics Intstitute - Publications
Di dunia nyata, objek sering menyembunyikan informasi mereka dan cara kerjanya. Hal ini juga berlaku pada standar perhitungan dalam berbagai kasus.
Dari sekian banyak kasus ada tujuh (7) masalah matematika yang paling sulit untuk dipecahkan yang dinyatakan oleh Clay Mathematics Intstitute pada tahun 2000.
Millenium Prize Problem diberikan dalam rangka menyambut millenium baru yang kadua. Dari tujuh (7) masalah yang diberikan disediakan hadiah total $ 7.000.000, dengan hadiah masing-masing masalah sebesar $ 1.000.000.
The Millennium Prize Problems are seven (7) problems in mathematics that were stated by the Clay Mathematics Institute on May 24, 2000. The problems are the :Sampai saat ini baru satu masalah yang dapat dipecahkan yaitu Poincaré Conjecture, masih ada enam (6) masalah yang masih belum terpecahkan:
- Birch and Swinnerton-Dyer conjecture,
- Hodge conjecture,
- Navier–Stokes existence and smoothness,
- P versus NP problem,
- Poincaré conjecture,
- Riemann hypothesis, and
- Yang–Mills existence and mass gap.
Salah satu sumber yang digunakan sebagai metode dasar saya gunakan cara pengintegrasian berbagai sumber data dari suatu penelitian yang hasilnya berupa matriks betikut:
Dengam metoda ini selanjutnya kita akan terapkan untuk mendapatkan korelasi antara kasus Poincare Conjecture dengan enam (6) kasus lainnya.
Dia juga mengerjakan teori-teori relativitas sebelum Einstein. Pada 1904, dia mengeluarkan pertanyaan yang sangat mendasar: apa bentuk dari ruang yang kita tempati ini ?
"Begitu Anda masuk ke dalam empat dimensi, Anda berbicara tentang ruang yang tidak dapat Anda visualisasikan. Cara termudah untuk memvisualisasikannya adalah dengan mempelajari apa yang terjadi dengan satu dimensi di dalam permukaan-permukaan dua dimensi", ujar Devlin, yang juga Direktur Eksekutif Pusat Studi Bahasa dan Informasi di Stanford.
Teorema yang diciptakan Poincare memang mampu terbukti dalam dunia-dunia imajinasi sehingga obyek-obyek memiliki empat, lima, atau lebih dimensi. Tetapi, tidak dengan tiga dimensi
Clay Mathematics Intstitute mengumukan pada tanggal 18 Maret 2010 bahwa masalah ini dipecahkan oleh Grigori Perelman dari St Petersburg, Rusia, namun beliau menolak untuk mendapatkan hadiahnya.
Para pengurus lembaga tersebut kemudian mengalihkan uang hadiah yang ditolak untuk kemajuan Matematika.
Konjektur Birch dan Swinnerton-Dyer dipilih sebagai salah satu dari 7 Millenium Problems yang dinyatakan oleh Clay Mathematics Institute.
Konjektur ini dinamai menurut matematikawan Bryan Birch dan Peter Swinnerton-Dyer yang mengembangkan pernyataan terkaan tersebut pada paruh pertama tahun 1960an dengan bantuan perhitungan mesin.
Dalam matematika, Konjektur Birch dan Swinnerton-Dyer (The Birch dan Swinnerton-Dyer Conjecture) menggambarkan serangkaian solusi rasional terhadap persamaan yang mendefinisikan kurva elips.
Ini adalah masalah terbuka di bidang teori bilangan dan secara luas diakui sebagai salah satu soal matematika yang paling menantang yang masih belum terpecahkan.
Penyataan dari terkaan tersebut adalah bahwa kurva eliptik memiliki banyak solusi rasional. Jadi, menyelesaikan persamaan seperti itu akan terurai ke satu angka tunggal untuk memberi tahu kita apakah ada banyak solusi tanpa batas atau tak terbatas.
Solusi ini terkait dengan perilaku fungsi Zeta yang terkait dengan ukuran kelompok titik rasional pada kurva.
Pada tahun 2017 ini, hanya kasus khusus dari terkaan tersebut yang telah terbukti.
Terkaannya sudah didukung oleh bukti eksperimental, namun bukti yang benar masih tersisa untuk diberikan, sehingga menjadikan konjektur ini terpilih sebagai salah satu dari Millennium Prize Problems.
Konjektur Hodge adalah salah satu yang paling sulit untuk dijelaskan.
Jika digambarkan secara sederhana sekalipun, masalahnya menanyakan apakah bentuk matematika kompleks bisa dibangun dari yang sederhana.
Sedikit banyak pertanyaannya mirip dengan objek bangunan yang tersusun dari blok mainan Lego.
Ide dasarnya adalah bertanya sejauh mana bentuk objek yang diberikan dapat didekati dengan menempelkan blok bangunan geometris sederhana dari dimensi yang meningkat.
Teknik ini menjadi populer dan mendapat generalisasi dalam banyak hal, memungkinkan para matematikawan untuk maju dalam mempelajari berbagai objek dalam penyelidikan mereka.
Namun, generalisasi akhirnya malah mengabaikan asal-usul geometris dan menjadi penting untuk menambahkan potongan yang tidak memiliki interpretasi geometris.
Konjektur Hodge mengatakan bahwa potongan-potongan yang disebut siklus Hodge ini sebenarnya hanyalah kombinasi dari potongan geometris yang disebut siklus aljabar.
Jika diuraikan dalam bahasa matematika, Konjektur Hodge adalah masalah utama yang belum terpecahkan dalam bidang geometri aljabar.
Konjektur / dugaan ini menghubungkan topologi aljabar dari suatu varietas aljabar kompleks nonsingular dan subvarietas dari varietas tersebut.
Secara spesifik, konjektur ini menyatakan bahwa de Rham cohomology tertentu termasuk ke dalam kelas aljabar, yaitu, perangkat yang termasuk ke topologi aljabar dan topologi diferensial adalah sejumlah Dualisme Poincaré dari kelas homologi subvarietasnya.
Konjektur ini dirumuskan oleh matematikawan Skotlandia William Vallance Douglas Hodge sebagai hasil kerja antara tahun 1930 hingga 1940 dalam rangka memperkaya deskripsi de Rham cohomology untuk memasukkan struktur tambahan yang hadir dalam kasus varietas aljabar kompleks.
Masalah ini hanya mendapat sedikit perhatian sebelum Hodge mempresentasikannya pada suatu kesempatan selama kongres matematikawan internasional pada tahun 1950, yang diadakan di Cambridge, Massachusetts, Amerika Serikat.
Mekanika kuantum adalah salah satu teori paling sukses dalam sejarah, memungkinkan kita untuk memahami perilaku materi dan energi pada tingkat partikel atom dan subatomik.
Sedikit mengherankan, mengingat penggunaan praktisnya yang begitu luas, para ahli matematika belum dapat membuktikan bahwa, dalam tiga dimensi, solusi selalu ada (eksistensi), atau jika memang ada, maka tidak mengandung keistimewaan.
Yang dan Mills memberikan kerangka penting untuk menggambarkan partikel elementer ini dengan menggunakan struktur matematis, dan teori ini memainkan peran penting dalam teori partikel tingkat dasar.
Teori tersebut mengemukakan bahwa partikel kuantum memiliki massa positif yang didefinisikan oleh “celah massa” untuk menggambarkan interaksi partikel elementer.
Teori ini telah diverifikasi lewat banyak eksperimen, namun hasilnya belum jelas bagi lembaga CMI. Dengan kata lain, partikel tidak bisa menjadi nol massa bahkan ketika partikel-partikel itu analog dengan foton tanpa massa.
Kesenjangan massa (mass gap) merupakan bagian penting untuk menjelaskan mengapa kekuatan nuklir sangat kuat dan mendekati jarak pendek dibandingkan dengan elektromagnetisme dan gravitasi.
Hal ini telah ditemukan oleh fisikawan melalui eksperimen dan divalidasi dengan simulasi komputer. Jadi Millennium Problem adalah bagaimana membangun teori matematika dan fisika umum untuk menjelaskan kesenjangan massa.
Persamaan Navier-Stokes juga sangat menarik dalam matematis murni. Soal ini disebut eksistensi Navier-Stokes dan masalah keluwesan (smooth).Persamaan Navier-Stokes sangat erat hubungannya dengan dinamika fluida yang merupakan subdisiplin dari mekanika fluida. Disiplin ilmu tersebut mempelajari fluida bergerak, yakni terutama yang berhubungan dengan cairan dan gas.
Penyelesaian dari masalah dinamika fluida biasanya melibatkan perhitungan banyak properti dari fluida, seperti kecepatan, tekanan, kepadatan, dan suhu, sebagai fungsi ruang dan wakt
Angka-angka prima selalu menjadi salah satu bidang penting yang menarik bagi matematikawan. Angka-angka ini hanya terbagi oleh diri mereka sendiri dan 1, yang sebenarnya membangun keseluruhan bilangan.
Dengan sangat pentingnya dalam matematika dan aplikasi, ada sejumlah besar minat untuk mengetahui bagaimana bilangan prima ini didistribusikan sepanjang garis angka.
Meskipun diyakini bahwa bilangan prima tidak mengikuti pola tertentu dibandingkan dengan bilangan asli lainnya, pada abad ke-19 matematikawan menemukan Teorema Perdana yang memberi perkiraan gagasan tentang jarak rata-rata antara bilangan prima.
Tapi, tetap tidak diketahui seberapa dekat distribusi sebenarnya tetap pada rata-rata itu.
- Rieman Hypothesis presentation by Numberphile (Youtube 17:04)
- Hipotesis Riemann Hampir Terpecahkan Tahun 2004
Bilangan prima itu dianalogikan sebagai atom-atom dari aritmetika yang merupakan kunci dari kode penyandian (kriptografi) internet.
Hipotesis Riemann, bagaimanapun, membatasi kemungkinan ini dengan menyarankan bahwa frekuensi bilangan prima berhubungan erat dengan perilaku fungsi yang rumit, yang dikenal sebagai fungsi Riemann Zeta.
Hipotesis tersebut menyatakan bahwa setiap nilai input pada persamaan yang menghasilkan nol (kecuali bilangan bulat negatif) jatuh pada garis yang sama persis.
Meskipun ini telah diperiksa untuk solusi 10 triliun pertama, masih memerlukan bukti yang ketat untuk setiap solusi menarik, menjadikannya salah satu Masalah Milenium yang belum terpecahkan.
Para matematikawan meyakini bahwa jika kita dapat membuktikan hipotesis Riemann dan mampu melihat pola dari bilangan prima, maka kita dapat dengan mudah melihat pola acak dari peristiwa alam seperti gempa, gunung meletus, dan tsunami.
Meski De Branges hampir menyelesaikannya pada tahun 2004, namun menurut Profesor Marcus Du Sautoy dari University of Oxford, hal yang belum ditemukan para ahli matematika adalah semacam spektrometer bilangan prima matematis sehingga bukti yang diumumkan De Branges kurang komprehensif
Satu lagi soal yang belum terpecahkan dalam 7 Millenium Problems yang dikemukakan Clay Mathematics Institute adalah solusi dari masalah P vs NP.
Isu yang mendasari masalah ini pertama kali dibahas pada tahun 1950-an, dalam sebuah surat dari John Forbes Nash Jr. ke National Security Agency, dan surat Kurt Gödel ke John von Neumann.
P (mudah ditemukan) Vs NP (mudah diperiksa) adalah masalah yang belum terpecahkan di dunia ilmu komputer teoritis. Secara sederhana, masalahnya pada dasarnya menanyakan hal ini: jika mudah untuk memastikan bahwa solusi atas sebuah masalah sudah benar, apakah ini juga mudah untuk memecahkan masalah?
“P” di sini adalah singkatan dari waktu polinomial, yaitu masalah yang lebih mudah dipecahkan oleh komputer dan “NP” adalah singkatan dari waktu polinomial nondeterministik, yaitu masalah yang tidak mudah dilakukan komputer, namun mudah untuk diperiksa. Salah satu contohnya adalah menemukan faktor utama bilangan besar.
Jika Anda memiliki semua daftar faktor yang mungkin, Anda dapat dengan mudah memperbanyaknya bersama-sama dan memeriksa apakah Anda bisa mendapatkan kembali nomor aslinya. Namun, tidak ada cara yang mungkin untuk menemukan faktor jumlah itu.
Matematikawan percaya bahwa tidak ada bukti yang memungkinkan hal itu terjadi, namun membuktikan hal yang sama itu sendiri adalah tugas yang menakutkan dan karena itu tetap merupakan salah satu Masalah Milenium yang belum terpecahkan.
Tujuannya adalah untuk mendapatkan metode yang sekiranya dapat diimplementasikan sebagai modul terhadap kasus lain berdasarkan suatu kaitan yang dapat dimanfaatkan.
Di pustaka ini Anda juga bisa telusuri solusi untuk salah satu kasus yang sudah dipecahkan, silahkan masukan input dengan nama kunci Grisha Perelman:
Jika kita pelajari kasus² ini jelas merupakan perkara yang extra rumit. Jika Anda memang punya bakat matematika sedari kecil tentu lebih mudah untuk paham.
Namun disini bakat saja tidak akan cukup karena begitu banyak sudah makalah diajukan dari berbagai sumber namun sudah sekian puluh tahun berlalu belum ada yang lain berhasil mengajukan bukti dari solusi.
Seperti kata pepatah, tidak ada ruginya untuk coba paham, minimal kita tahu bahwa ada kasus semacam ini. Dengan demikian kita akan lakukan penelusuran ini dimulai dengan kasus yang sudah dipecahkan yaitu Poincare Conjecture.
"If God speaks to man, he undoubtedly uses the language of mathematics."
(Henri Poincaré)
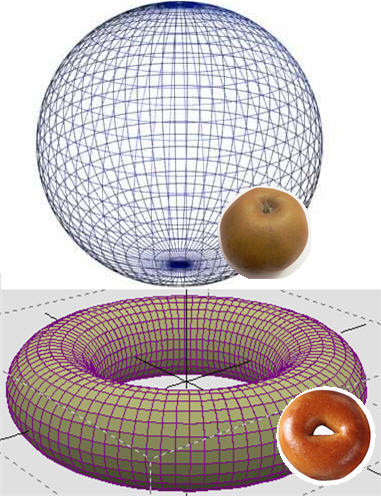
Poincaré Conjecture, yang disarankan oleh Henri Poincaré pada tahun 1904, mengusulkan hasil analog untuk manifold tiga dimensi: manifold kompak tiga dimensi yang terhubung sederhana harus berupa bola .
Pada Kongres Internasional Matematika 2006, Grigori Perelman dianugerahi Medali Fields untuk buktinya, meskipun ia menolak untuk menerimanya.
Versi dimensi tinggi dari Poincaré Conjecture, dengan lebih banyak ruang untuk melakukan konstruksi geometris, lebih mudah. Stephen Smale membuktikan dugaan analog untuk dimensi setidaknya 5 dan memenangkan Fields Medal pada tahun 1966. Michael Freedman membuktikan kasus 4-dimensi dan memenangkan medali Fields pada tahun 1986.
si dimensi tinggi dari Poincaré Conjecture, dengan lebih banyak ruang untuk melakukan konstruksi geometris, lebih mudah. Stephen Smale membuktikan dugaan analog untuk dimensi setidaknya 5 dan memenangkan Fields Medal pada tahun 1966. Michael Freedman membuktikan kasus 4-dimensi dan memenangkan medali Fields pada tahun 1986.
Gagasan dasar dari bukti Perelman, menurut Richard Hamilton, adalah untuk memulai dengan manifold tiga-kompak yang terhubung dan membiarkannya menyusut pada setiap titik pada setiap arah dengan kecepatan yang sebanding dengan kelengkungan Ricci -nya . Jika Anda dapat menunjukkan bahwa Anda akhirnya berakhir dengan bola bundar, dengan bola-bola lain mungkin terjepit di sepanjang jalan, Anda dapat menyimpulkan bahwa Anda harus memulai dengan bola (cacat).
Kesulitan mendasar adalah untuk mendapatkan kontrol atas pembentukan singularitas. Untuk memfokuskan perhatian tentang hal yang menjadi perhatian, Perelman [Sect.] memberikan kepadatan berlipat ganda tentang titik itu dan memungkinkan aliran metrik oleh kelengkungan Ricci umum yang terkait, Ric ψ 18,3 ( 4 ). Jika seseorang memperbaiki ukuran, maka kerapatan berkembang sebagai persamaan panas terbalik yang dimodifikasi dan mendekati fungsi delta pada hal . Monotonitas energinya yang umum sekarang menyediakan informasi lokal yang diperlukan alih-alih informasi global yang biasa. (Sebenarnya, dalam buktinya, untuk memfasilitasi operasi, Perelman [Bagian] pindah ke versi lokal kepadatan yang disebut fungsi panjang.)
Hebatnya, modulo difeomorfisme , aliran Ricci yang digeneralisasi ini setara dengan aliran Ricci standar. Seperti yang dikatakan Perelman, “Fakta yang luar biasa di sini adalah bahwa pilihan [kepadatan] yang berbeda mengarah ke aliran yang sama, hingga difeomorfisme; yaitu, pilihan [kepadatan] analog dengan pilihan pengukur. ” Ini berarti bahwa selama pembuktian, seseorang dapat memilih kepadatan apa pun untuk kenyamanan. Singkatnya, manifold dengan kepadatan menyediakan konteks teknis yang nyaman untuk menerapkan difeomorfisme untuk memusatkan perhatian pada wilayah yang menjadi perhatian.
Selain manifold umum dengan kepadatan, contoh utama ruang Gauss membuat penampilan penting dalam bukti Perelman. Secara khusus, ketimpangan isoperimetri pada ruang Gauss dalam bentuk fungsional, yang dikenal sebagai ketimpangan Sobolev logaritmik Gaussian, merupakan unsur teknis yang penting.
Manifol umum dengan kepadatan belum muncul di sebagian besar paparan karya Perelman. Ini sebagian karena mereka muncul hanya di bagian pengantar dan digantikan oleh fungsi panjangnya di bukti yang sebenarnya. Ini juga sebagian karena manifold dengan kepadatan tidak begitu akrab dengan komunitas matematika sebagaimana mestinya. Mereka muncul dalam kalimat pertama dari tubuh kertas Perelman, di mana ia mulai dengan mempertimbangkan bermacam-macam dengan kepadatan e - f dan kelengkungan skalar R :
Pertimbangkan fungsional F = ∫ M ( R + | ∇ f | 2 ) e - f dV untuk metrik Riemannian g ij dan fungsi f pada manifold tertutup M .
Anderson, dalam survei Pemberitahuannya , membuat komentar berikut tentang diskusi Perelman tentang aliran Ricci dalam manifold dengan kepadatan:
Ternyata, mengingat setiap metrik awal g (0) dan t > 0, fungsi [kerapatan] f ... dapat ditentukan secara bebas di g ( t )…. Perelman kemudian menggunakan kebebasan ini untuk menyelidiki geometri g ( t ) dengan pilihan f . Sebagai contoh, ia menunjukkan dengan studi yang sangat sederhana tentang bentuk [energi] F bahwa keruntuhan atau noncollapse dari metrik g ( t ) di dekat titik x 0 dapat dideteksi dari ukuran F dengan memilih f untuk menjadi perkiraan untukfungsi delta berpusat di x . Semakin runtuh g ( t ) dekat x , semakin negatif nilai F . Runtuhnya metrik g ( t ) pada skala apa pun dalam waktu yang terbatas kemudian dikesampingkan dengan menggabungkan ini dengan fakta bahwa F fungsional meningkat di sepanjang aliran Ricci. Bahkan, argumen ini dilakukan sehubungan dengan fungsional invarian skala yang agak lebih rumit daripada F ; termotivasi oleh analogi tertentu dalam fisika statistik, Perelman menyebut ini fungsional entropi .
Perelman, dalam kutipan berikut dari Pendahuluannya, merujuk pada hasil nonkolaps dari §4 ini. Dia juga menyebutkan penggunaan dalam § 3 Gaussian isoperimetric kesenjangannya untuk membuktikan bahwa Anda tidak mendapatkan periodisitas alih-alih perilaku pembatasan yang diinginkan.
Kami membuktikan bahwa aliran Ricci, yang dianggap sebagai sistem dinamis pada ruang metrik Riemannian modulo difeomorfisme dan penskalaan, tidak memiliki orbit periodik nontrivial. Kasus metrik yang mudah (dan diketahui) dengan kelengkungan skalar minimum negatif diperlakukan dalam §2; kasus lainnya dibahas dalam §3, menggunakan rumus monotonisitas utama kami (3.4) dan ketidaksetaraan Sobolev logaritmik Gaussian, karena L. Gross. Dalam §4 kami menerapkan rumus monotonisitas kami untuk membuktikan bahwa untuk solusi yang halus pada interval waktu yang terbatas , jari-jari injeksi pada setiap titik dikontrol oleh lengkungan pada titik-titik terdekat. Hasil ini menghilangkan batu sandungan utama dalam pendekatan Hamilton untuk geometriisasi.
Dalam matematika, dugaan Hodge adalah masalah besar yang belum terpecahkan dalam geometri aljabar yang menghubungkan topologi aljabar dari variasi aljabar kompleks non-singular dengan subvarietasnya.
Lebih khusus lagi, dugaan tersebut menyatakan bahwa kelas kohomologi de Rham tertentu bersifat aljabar; yaitu, mereka adalah jumlah dual Poincaré dari kelas - kelas homologi subvarieties.
Sementara permukaan tertutup telah diklasifikasikan terutama oleh Bernhard Riemann, klasifikasi manifold tertutup memiliki hubungan yang dalam dengan dugaan Poincaré.
Pada tahun 1982, William Thurston, mungkin topologi terhebat abad ke-20, menduga bahwa geometri dari bermacam-macam 3-manifold dapat diklasifikasikan sebagai salah satu dari 8 kemungkinan geometri.
Bukti Perelman, bersama dengan dugaan Poincaré, menjawab dugaan Thurston secara positif.
Dalam bidang matematika teori graf, Jalur Hamiltonian (atau jalur yang dapat dilacak ) adalah jalur dalam grafik tidak berarah atau terarah yang mengunjungi setiap simpul tepat sekali.
Sebuah siklus Hamiltonian (atau sirkuit Hamilton ) adalah jalur Hamiltonian yang merupakan siklus . 
Menentukan apakah suatu jalur dan siklus ada dalam grafik adalah masalah jalur Hamiltonian, yang merupakan NP-complete sehingga masuk dalam salah satu kasus dari Masalah P vs NP.
Twin Primes:
(5,7), (11,13), (17,19)
layer| i | f
-----+-----+------
| 1 | (5) -------
1 +-----+ |
| 2 | (7) |
-----+-----+------ |
| 3 | (11) ‹--3x--
2 +-----+ |
| 4 | (13) |
-----+-----+------ |
| 5 | (17) ‹--2x--
3 +-----+
| 6 | (19)
-----+-----+------
Permutation:
66 = 6 & 6
6 + 6 = 12
5 + 7 = 12 = d(3)
11 + 13 = 24 = d(6)
17 + 19 = 6 x 6 = d(9)
6 + 6 » d(3,6,9) » 6 x 6
Sekian.
SALAM Sukses!
© Chetabahana Project
