ENH: possible 3000x speedup for high aspect-ratio matrices by SVD on `A*A.T`

[EngrStudent]

Proposed new feature or change:

(Scope) This suggestion is to modify "numpy.linalg.svd" and should give, for matrices where one axis is much larger than the other no less than a 20x speedup, and up to a 10,000x speedup.

If you have a matrix that is say 200 rows by 8 million columns, then when you multiply it by its transpose the result is 200x200 matrix. If you perform SVD on that you can determine both the left-singular vectors and the squares of the eigenvalues. It is symmetric and real, so according to this it is likely Hermitian.

(Versions) I am using numpy version 1.19.2, on python 3.8.12 in the following.

Here is example code to show the performance difference (using JuPyTeR):

import numpy as np
print(np.__version__)
---
A = np.random.rand(int(1e2), int(1e4))
AA = np.matmul(A,np.transpose(A))
---
%%timeit -n 3 -r 3
u1, s1, vt1 = np.linalg.svd(A)
---
u1, s1, vt1 = np.linalg.svd(A)
---
%%timeit -n 3 -r 3
u2, s2, vt2 = np.linalg.svd(AA)

s2b = np.sqrt(s2)                    #get eigens
rot_mat = np.matmul(u2, u1.T)        #get rot for u2 --> u1
u2_in_u1 = np.matmul(rot_mat, u2)    #perform rotation
B = np.matmul(np.diag(s2b),u2_in_u1) #get u1*s
B_inv = np.linalg.pinv(B)            #find pinv 
vt2b = np.matmul(B_inv,A)            #isolate vt in u1 coords

the horizontal '---' indicate cell breaks

Here is a screenshot of the timing difference:

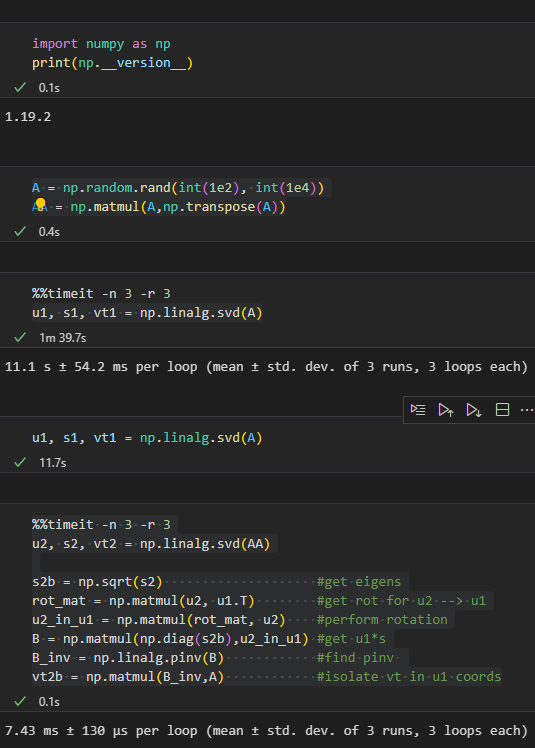
The image shows something like an order of 3-decade speedup for the operation. All the commented code in the SVD for AA, except for the square root, is extra. It maps V2 into V1. This is a strong over-estimate of how long it takes.

here is the code that shows the eigenvalues are compatible:

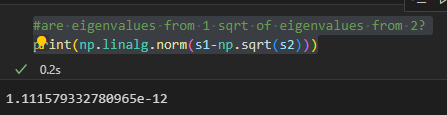
#are eigenvalues from 1 sqrt of eigenvalues from 2?
print(np.linalg.norm(s1-np.sqrt(s2)))

Here is the output:

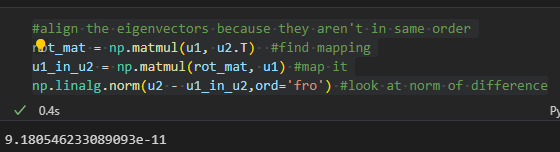
Here is the code that shows the left singular vectors are compatible:

#align the eigenvectors because they aren't in same order
rot_mat = np.matmul(u1, u2.T)  #find mapping
u1_in_u2 = np.matmul(rot_mat, u1) #map it
np.linalg.norm(u2 - u1_in_u2,ord='fro') #look at norm of difference

Here is the image of the output

So what about the reduced dim options?

When I look for reduced dims, it gives this:

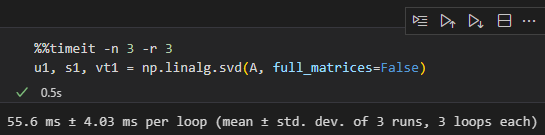
This takes 55.6/7.43 = 7.48 times longer to compute. I should be able to get the left singular matrix for the first decomposition, the rotation, using the results of the simpler matrix in less time.

If the matrix is scaled the other way, then some algebra and transposes should still yield similar speedups.

If the matrix is specified as Hermitian, (as symmetric and real should be) then the compute is done even more quickly.

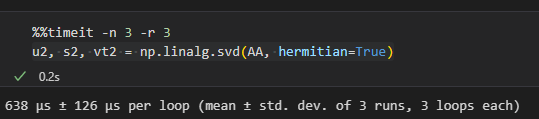
I don't think every rectangular matrix multiplied by its transpose is Hermitian. This form of the real-valued A*A.T here can be contrived as a projection matrix, so it might be Hermitian.

(Disclaimer) I'm not sure if this is currently being done, but I think it isn't because of the decent multiple differences in timing (shown below). It has been some time since I took linear algebra, and so perhaps I am not as fresh as I could be there.

[MatteoRaso]

I don't think every rectangular matrix multiplied by its transpose is Hermitian.

It is if the elements are real. (Proof: If a real square matrix is symmetric, it's Hermitian. (A @ A.T).T = A.T.T @ A.T = A @ A.T, so it's symmetric).

I'm not entirely sure what you're suggesting, though? Is it an improvement for numpy.linalg.svd? I've also noticed that your second part of the code uses the results from the first part, so the second part is necessarily longer, even if timeit says otherwise. You also didn't include the time it takes to get AA, which probably isn't a whole lot of time, but it's still not negligible.

[EngrStudent]

In the upper image you can see that I naïvely put in the matrix and it takes 10 seconds. When I put in the projection matrix, which is 100 x 100, it runs way faster, in 7.43 ms. Its a ~3000x speed up. If it is Hermitian then it runs in under 1 ms, and is a ~10,000x speed up.

If you test the shape of the input matrix and it has a relatively high aspect ratio, then you can perform SVD on the substantially smaller “projection matrix” and get some thing that runs maybe thousands of times faster.

The rest of my code it’s about showing the results are equivalent.

I was surprised that even with the extra operations in python it was so much faster.

I thought but I’m not sure that one of the requirements to be hermitian is that it was idempotent. That would be A*A.T = A, And I think there are symmetric matrices that are not idempotent.

[ilayn]

The speed up is coming from not computing the right eigenvectors.

The main feature request which is also requested over SciPy too is that the API should have separated the options compute_u and compute_v such that you can select which ones to compute. Then you can still have the speed up with svd(A, compute_v=False) and it won't go through the agonizing 10000x10000 array creation (which is what it takes 10 seconds to generate).

So in that regard, you are creating a not so precise work-around to avoid the right singular vectors.

PS: When you have symmetric/hermitian arrays, use eigh not svd as they are equivalent but eigh specializes in computing things more precisely for sym/her arrays.

[charris]

IIRC, the problem is the choice of default value of full_matrices=True, which nobody ever wants :) Well, maybe it is useful for some things ...

[EngrStudent]

IIRC, the problem is the choice of default value of full_matrices=True, which nobody ever wants :) Well, maybe it is useful for some things ...

It is, in fact, useful for some things. ;)

The speed up is coming from not computing the right eigenvectors.

The main feature request which is also requested over SciPy too is that the API should have separated the options compute_u and compute_v such that you can select which ones to compute. Then you can still have the speed up with svd(A, compute_v=False) and it won't go through the agonizing 10000x10000 array creation (which is what it takes 10 seconds to generate).

So in that regard, you are creating a not so precise work-around to avoid the right singular vectors.

PS: When you have symmetric/hermitian arrays, use eigh not svd as they are equivalent but eigh specializes in computing things more precisely for sym/her arrays.

Thank you for the suggestion, I would like to look into that.

Question: does knowing the left eigenvectors and the eigenvalues speed up the computation of the right eigenvectors? There are fewer unknowns, and matrix operations on the much smaller matrices should be much faster.

[charris]

It is, in fact, useful for some things. ;)

The only thing I can think of is a basis of the orthogonal compliment of the range space. Projection on the orthogonal complement doesn't need it. For square matrices there is no difference, it is the skinny ones where it matters.