A* Search Algorithm in Javascript

a simple implementation of A* algorithm in javascript

Example

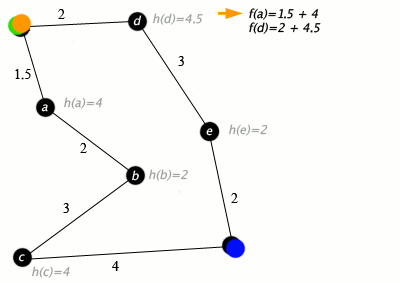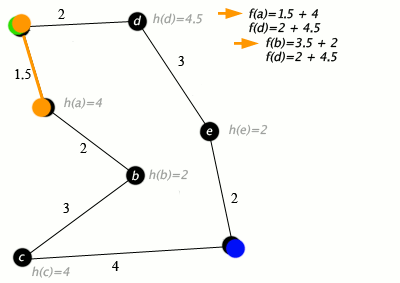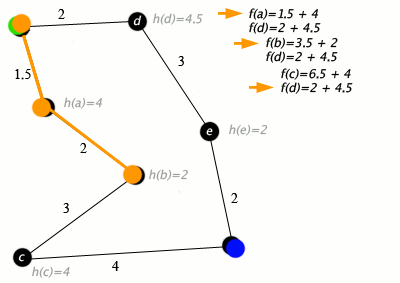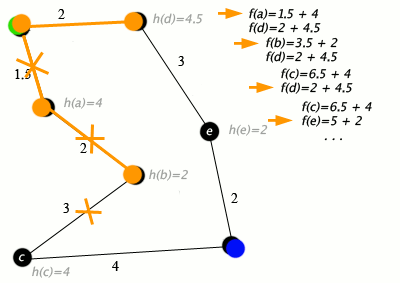
An example of an A* algorithm in action where nodes are cities connected with roads and h(x) is the straight-line distance to target point: An example of A* algorithm in action (nodes are cities connected with roads, h(x) is the straight-line distance to target point) Green: Start, Blue: Target, Orange: Visited

Key: green: start; blue: goal; orange: visited

• Demo

The following pseudocode describes the algorithm

function A*(start, goal)
    // The set of nodes already evaluated
    closedSet := {}

    // The set of currently discovered nodes that are not evaluated yet.
    // Initially, only the start node is known.
    openSet := {start}

    // For each node, which node it can most efficiently be reached from.
    // If a node can be reached from many nodes, cameFrom will eventually contain the
    // most efficient previous step.
    cameFrom := an empty map

    // For each node, the cost of getting from the start node to that node.
    gScore := map with default value of Infinity

    // The cost of going from start to start is zero.
    gScore[start] := 0

    // For each node, the total cost of getting from the start node to the goal
    // by passing by that node. That value is partly known, partly heuristic.
    fScore := map with default value of Infinity

    // For the first node, that value is completely heuristic.
    fScore[start] := heuristic_cost_estimate(start, goal)

    while openSet is not empty
        current := the node in openSet having the lowest fScore[] value
        if current = goal
            return reconstruct_path(cameFrom, current)

        openSet.Remove(current)
        closedSet.Add(current)

        for each neighbor of current
            if neighbor in closedSet
                continue		// Ignore the neighbor which is already evaluated.

            if neighbor not in openSet	// Discover a new node
                openSet.Add(neighbor)
            
            // The distance from start to a neighbor
            tentative_gScore := gScore[current] + dist_between(current, neighbor)
            if tentative_gScore >= gScore[neighbor]
                continue		// This is not a better path.

            // This path is the best until now. Record it!
            cameFrom[neighbor] := current
            gScore[neighbor] := tentative_gScore
            fScore[neighbor] := gScore[neighbor] + heuristic_cost_estimate(neighbor, goal) 

    return failure

function reconstruct_path(cameFrom, current)
    total_path := [current]
    while current in cameFrom.Keys:
        current := cameFrom[current]
        total_path.append(current)
    return total_path

Wikipedia

you can get a lot of information about this algorithm Here

Built With

• NodeJS - for making a simple http server [optinal to use it]
• p5.js - p5.js a JS client-side library for creating graphic and interactive experiences, based on the core principles of Processing.

Authors

• Shady Khalifa - Initial work

See also the list of contributors who participated in this project.

License

This project is licensed under the MIT License - see the LICENSE.md file for details