|
| 1 | +### 题目描述 |
| 2 | + |
| 3 | +这是 LeetCode 上的 **[863. 二叉树中所有距离为 K 的结点](https://leetcode-cn.com/problems/all-nodes-distance-k-in-binary-tree/solution/gong-shui-san-xie-yi-ti-shuang-jie-jian-x6hak/)** ,难度为 **中等**。 |
| 4 | + |
| 5 | +Tag : 「图论 BFS」、「图论 DFS」、「二叉树」 |
| 6 | + |
| 7 | + |
| 8 | + |
| 9 | +给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 K 。 |
| 10 | + |
| 11 | +返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。 |
| 12 | + |
| 13 | + |
| 14 | +示例 1: |
| 15 | +``` |
| 16 | +输入:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2 |
| 17 | +
|
| 18 | +输出:[7,4,1] |
| 19 | +
|
| 20 | +解释: |
| 21 | +所求结点为与目标结点(值为 5)距离为 2 的结点, |
| 22 | +值分别为 7,4,以及 1 |
| 23 | +``` |
| 24 | +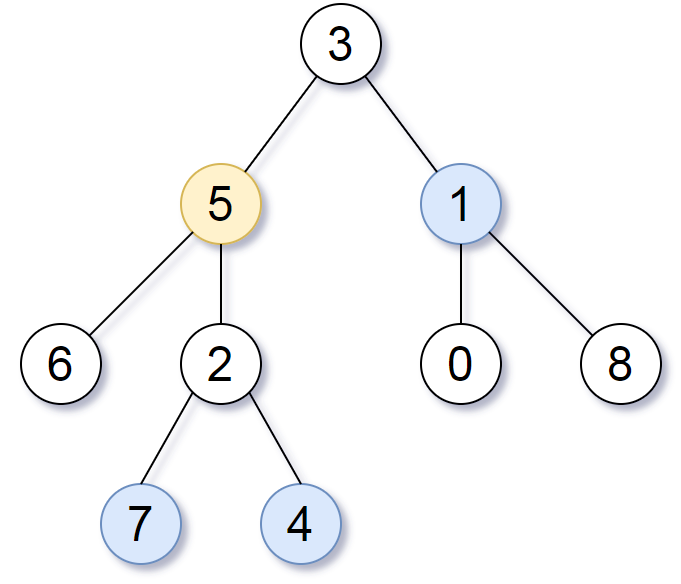 |
| 25 | + |
| 26 | +注意,输入的 "root" 和 "target" 实际上是树上的结点。 |
| 27 | +上面的输入仅仅是对这些对象进行了序列化描述。 |
| 28 | + |
| 29 | +提示: |
| 30 | +* 给定的树是非空的。 |
| 31 | +* 树上的每个结点都具有唯一的值 0 <= node.val <= 500 。 |
| 32 | +* 目标结点 target 是树上的结点。 |
| 33 | +* 0 <= K <= 1000. |
| 34 | + |
| 35 | +--- |
| 36 | + |
| 37 | +### 基本分析 |
| 38 | + |
| 39 | +显然,如果题目是以图的形式给出的话,我们可以很容易通过「`BFS` / 迭代加深」找到距离为 $k$ 的节点集。 |
| 40 | + |
| 41 | +而树是一类特殊的图,我们可以通过将二叉树转换为图的形式,再进行「`BFS` / 迭代加深」。 |
| 42 | + |
| 43 | +由于二叉树每个点最多有 $2$ 个子节点,点和边的数量接近,属于稀疏图,因此我们可以使用「邻接表」的形式进行存储。 |
| 44 | + |
| 45 | +建图方式为:对于二叉树中相互连通的节点(`root` 与 `root.left`、`root` 和 `root.right`),建立一条无向边。 |
| 46 | + |
| 47 | +建图需要遍历整棵树,使用 `DFS` 或者 `BFS` 均可。 |
| 48 | + |
| 49 | +由于所有边的权重均为 $1$,我们可以使用 「`BFS` / 迭代加深」 找到从目标节点 `target` 出发,与目标节点距离为 $k$ 的节点,然后将其添加到答案中。 |
| 50 | + |
| 51 | +>一些细节:利用每个节点具有唯一的值,我们可以直接使用节点值进行建图和搜索。 |
| 52 | +
|
| 53 | + |
| 54 | +--- |
| 55 | + |
| 56 | +### 建图 + `BFS` |
| 57 | + |
| 58 | +由「基本分析」,可写出「建图 + `BFS`」的实现。 |
| 59 | + |
| 60 | + |
| 61 | + |
| 62 | +代码: |
| 63 | +```Java [] |
| 64 | +class Solution { |
| 65 | + int N = 1010, M = N * 2; |
| 66 | + int[] he = new int[N], e = new int[M], ne = new int[M]; |
| 67 | + int idx; |
| 68 | + void add(int a, int b) { |
| 69 | + e[idx] = b; |
| 70 | + ne[idx] = he[a]; |
| 71 | + he[a] = idx++; |
| 72 | + } |
| 73 | + boolean[] vis = new boolean[N]; |
| 74 | + public List<Integer> distanceK(TreeNode root, TreeNode t, int k) { |
| 75 | + List<Integer> ans = new ArrayList<>(); |
| 76 | + Arrays.fill(he, -1); |
| 77 | + dfs(root); |
| 78 | + Deque<Integer> d = new ArrayDeque<>(); |
| 79 | + d.addLast(t.val); |
| 80 | + vis[t.val] = true; |
| 81 | + while (!d.isEmpty() && k >= 0) { |
| 82 | + int size = d.size(); |
| 83 | + while (size-- > 0) { |
| 84 | + int poll = d.pollFirst(); |
| 85 | + if (k == 0) { |
| 86 | + ans.add(poll); |
| 87 | + continue; |
| 88 | + } |
| 89 | + for (int i = he[poll]; i != -1 ; i = ne[i]) { |
| 90 | + int j = e[i]; |
| 91 | + if (!vis[j]) { |
| 92 | + d.addLast(j); |
| 93 | + vis[j] = true; |
| 94 | + } |
| 95 | + } |
| 96 | + } |
| 97 | + k--; |
| 98 | + } |
| 99 | + return ans; |
| 100 | + } |
| 101 | + void dfs(TreeNode root) { |
| 102 | + if (root == null) return; |
| 103 | + if (root.left != null) { |
| 104 | + add(root.val, root.left.val); |
| 105 | + add(root.left.val, root.val); |
| 106 | + dfs(root.left); |
| 107 | + } |
| 108 | + if (root.right != null) { |
| 109 | + add(root.val, root.right.val); |
| 110 | + add(root.right.val, root.val); |
| 111 | + dfs(root.right); |
| 112 | + } |
| 113 | + } |
| 114 | +} |
| 115 | +``` |
| 116 | +* 时间复杂度:通过 `DFS` 进行建图的复杂度为 $O(n)$;通过 `BFS` 找到距离 $target$ 为 $k$ 的节点,复杂度为 $O(n)$。整体复杂度为 $O(n)$ |
| 117 | +* 空间复杂度:$O(n)$ |
| 118 | + |
| 119 | +--- |
| 120 | + |
| 121 | +### 建图 + 迭代加深 |
| 122 | + |
| 123 | +由「基本分析」,可写出「建图 + 迭代加深」的实现。 |
| 124 | + |
| 125 | +迭代加深的形式,我们只需要结合题意,搜索深度为 $k$ 的这一层即可。 |
| 126 | + |
| 127 | + |
| 128 | + |
| 129 | +代码: |
| 130 | +```Java |
| 131 | +class Solution { |
| 132 | + int N = 1010, M = N * 2; |
| 133 | + int[] he = new int[N], e = new int[M], ne = new int[M]; |
| 134 | + int idx; |
| 135 | + void add(int a, int b) { |
| 136 | + e[idx] = b; |
| 137 | + ne[idx] = he[a]; |
| 138 | + he[a] = idx++; |
| 139 | + } |
| 140 | + boolean[] vis = new boolean[N]; |
| 141 | + public List<Integer> distanceK(TreeNode root, TreeNode t, int k) { |
| 142 | + List<Integer> ans = new ArrayList<>(); |
| 143 | + Arrays.fill(he, -1); |
| 144 | + dfs(root); |
| 145 | + vis[t.val] = true; |
| 146 | + find(t.val, k, 0, ans); |
| 147 | + return ans; |
| 148 | + } |
| 149 | + void find(int root, int max, int cur, List<Integer> ans) { |
| 150 | + if (cur == max) { |
| 151 | + ans.add(root); |
| 152 | + return ; |
| 153 | + } |
| 154 | + for (int i = he[root]; i != -1; i = ne[i]) { |
| 155 | + int j = e[i]; |
| 156 | + if (!vis[j]) { |
| 157 | + vis[j] = true; |
| 158 | + find(j, max, cur + 1, ans); |
| 159 | + } |
| 160 | + } |
| 161 | + } |
| 162 | + void dfs(TreeNode root) { |
| 163 | + if (root == null) return; |
| 164 | + if (root.left != null) { |
| 165 | + add(root.val, root.left.val); |
| 166 | + add(root.left.val, root.val); |
| 167 | + dfs(root.left); |
| 168 | + } |
| 169 | + if (root.right != null) { |
| 170 | + add(root.val, root.right.val); |
| 171 | + add(root.right.val, root.val); |
| 172 | + dfs(root.right); |
| 173 | + } |
| 174 | + } |
| 175 | +} |
| 176 | +``` |
| 177 | +* 时间复杂度:通过 `DFS` 进行建图的复杂度为 $O(n)$;通过迭代加深找到距离 $target$ 为 $k$ 的节点,复杂度为 $O(n)$。整体复杂度为 $O(n)$ |
| 178 | +* 空间复杂度:$O(n)$ |
| 179 | + |
| 180 | + |
| 181 | +--- |
| 182 | + |
| 183 | +### 最后 |
| 184 | + |
| 185 | +这是我们「刷穿 LeetCode」系列文章的第 `No.863` 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先将所有不带锁的题目刷完。 |
| 186 | + |
| 187 | +在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。 |
| 188 | + |
| 189 | +为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。 |
| 190 | + |
| 191 | +在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。 |
| 192 | + |
0 commit comments