DAE solver using IDA and events: solution sol seem to store wrong values

[MartinOtter]

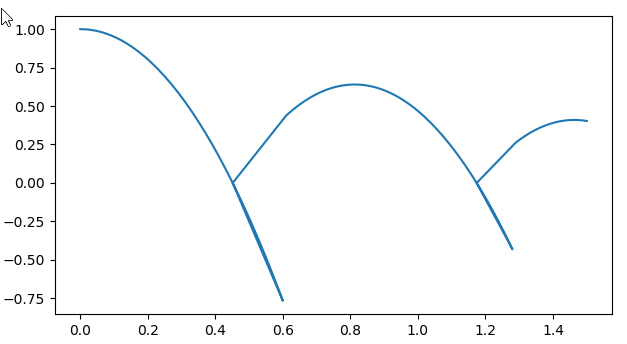
The following model defines a bouncing ball problem as DAE and uses IDA to solve it:

module Test_bouncingBall2

using DifferentialEquations, PyPlot, Sundials

function derivative(du,u,p,t)
    du[1] = u[2]
    du[2] = -9.81
end

function f(res,du,u,p,t)
  derivative(res,u,p,t)
  res[1] = du[1] - res[1]
  res[2] = du[2] - res[2]
end

function condition(u,t,integrator) # Event when event_f(u,t) == 0
 z = u[1]  + 1e-12
 println("condition called at time = ", t, ", z = ", z)
 return z
end

function affect_neg(integrator)
  println("time = ", integrator.t, ", h = ", integrator.u[1])
  integrator.u[2] = -0.8*integrator.u[2]
  derivative(integrator.du, integrator.u, integrator.p, integrator.t)
end

cb = ContinuousCallback(condition,nothing,affect_neg! = affect_neg)

u0 = [1.0,0.0]
du0= [0.0,-9.81]
tspan = (0.0,1.5)
prob = DAEProblem(f,du0,u0,tspan)
sol = solve(prob,IDA(),saveat=0.01,callback=cb)

figure(1)
clf()
plot(sol.t, getindex.(sol.u, 1), label="h")

end

The resulting plot is:

This seems to indicate that the DAE solver stores the time instant of the IDA step at which a zero crossing condition is detected, but then does not delete this time instant from sol, once the event is triggered (between the previous and the current step time instant) and affect! or affect_neg! is called.

[ChrisRackauckas]

This seems to indicate that the DAE solver stores the time instant of the IDA step at which a zero crossing condition is detected, but then does not delete this time instant from sol, once the event is triggered (between the previous and the current step time instant) and affect! or affect_neg! is called.

Indeed that looks to be the case.

[ChrisRackauckas]

Though it shouldn't be storing those values in the first place. Hmmm...