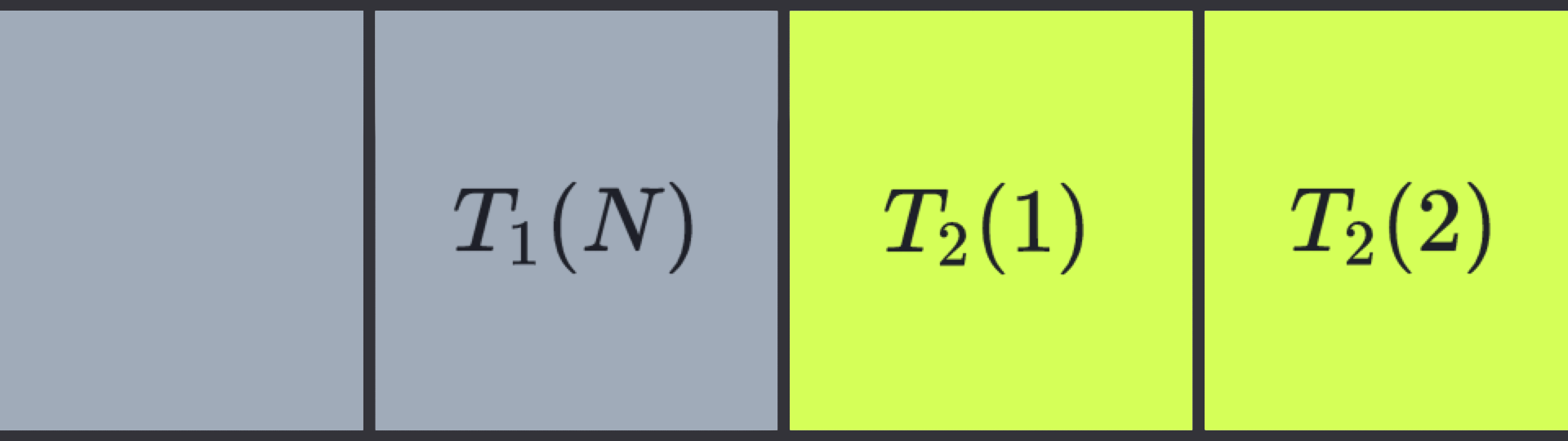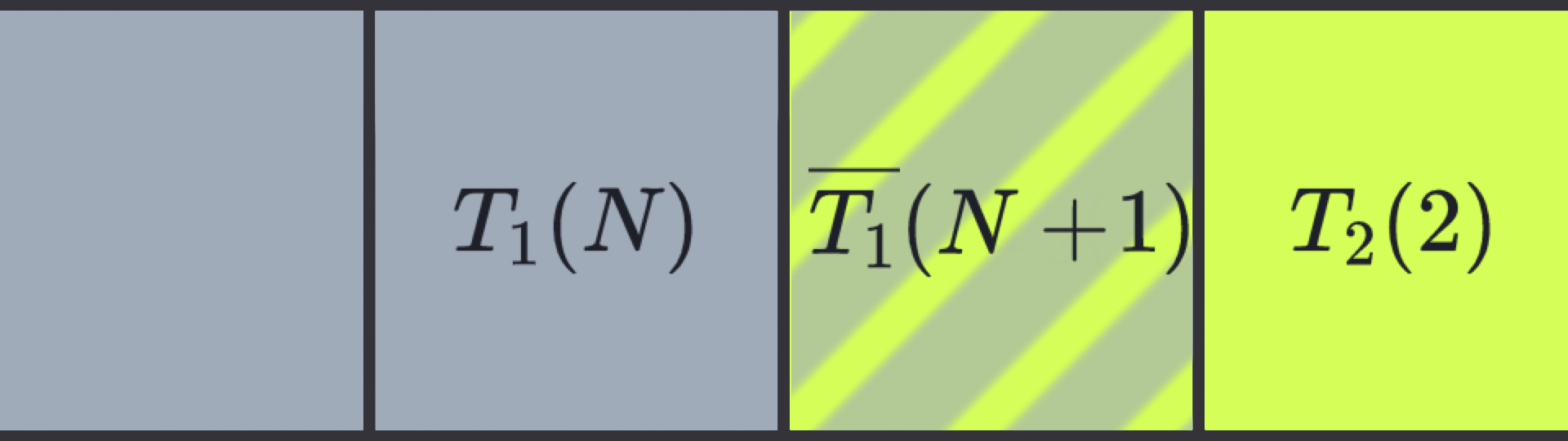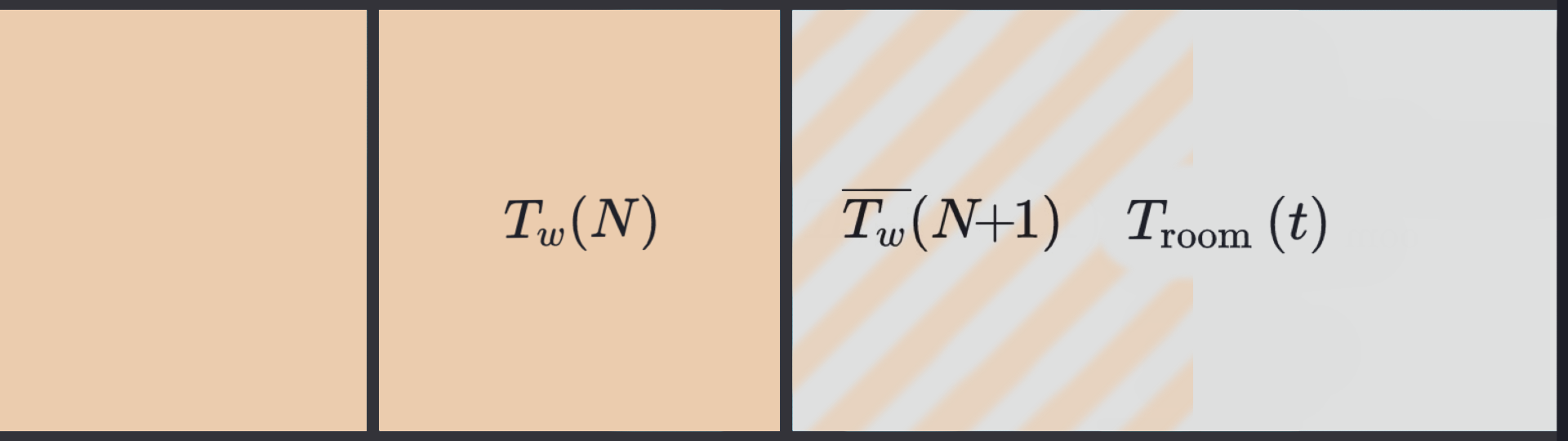• Méthode Physique de résolution
  • Introduction
    • Hypothèses
    • Grandeurs utilisées
  • Modélisation du problème
    • Intérieur du MCP
    • Interface Solide/MCP
    • Interface Air/MCP
  • Résolution numérique
    • Matrice Globale
    • Itérations internes
    • Optimisation
• Programme Python
  • Fonctionnement du programme Python
    • Librairies\Modules
    • Configuration
    • Simulation
    • Résultats

Introduction au problème

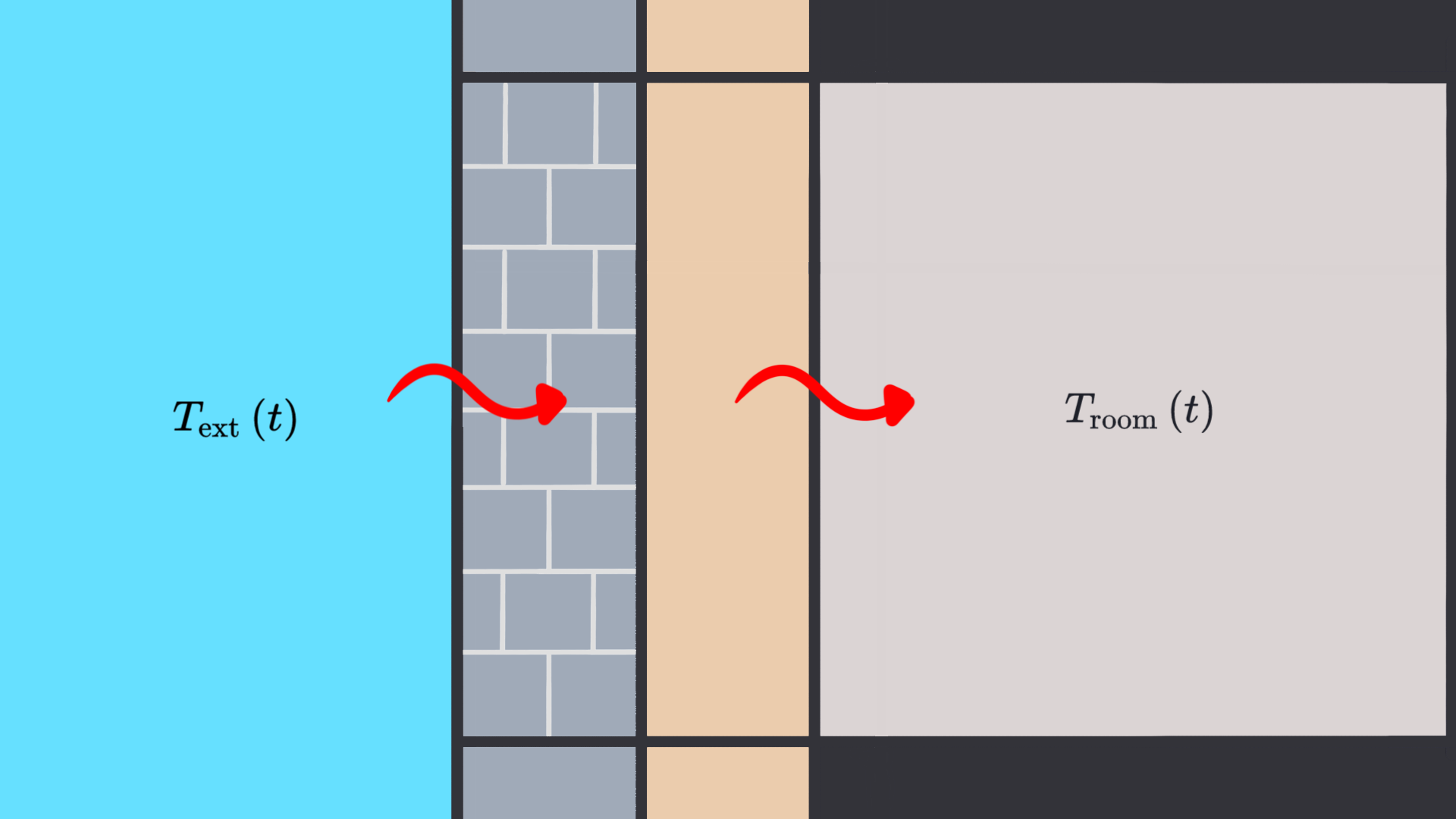
On étudie l’influence des matériaux à changement de phase (MCP) sur l’isolation des batiments.

Illustration du problème. On pose un axe x horizontal, orienté de la gauche vers la droite

Hypothèses

• Les transferts thermiques sont supposés unidimensionnels
• La température extérieure est variable dans le temps, elle est connue
• La température de la pièce ne varie pas au cours du temps, elle est connue
• Les échanges aux interfaces air/solide sont gérés par la loi de Newton
• Le mur est composite et peut comporter plusieurs MCP
• Les propriétés thermodynamiques du MCP sont supposées constantes dans sa phase solide ou dans sa phase liquide (la conductivité, la capacité calorifique volumique, la masse volumique ne dépendent que de l’état solide/liquide du MCP et non de sa température, pression, etc…)

Grandeurs utilisées

Symbole	Signification	Unité
$H$	Enthalpie volumique	$J.m^{-3}$
$h$	Enthalpie sensible volumique	$J.m^{-3}$
$T$	Température	$K$
$\lambda$	Conductivité thermique	$W.m^{-1}.K^{-1}$
$\rho$	Masse volumique	$kg.m^{-3}$
$c$	Capacité calorifique massique	$J.k{g}^{-1}$
$L$	Chaleur latente massique	$J.k{g}^{-1}$
$f$	fraction fondue, liquide	SU
$h_{int}$, $h_{ext}$	Coefficients de convection	$W.m^{-2}.K^{-1}$

---

Modélisation du problème

On scinde le transfert de chaleur en trois parties:

• à l’intérieur du MCP
• à l’interface Solide/MCP
• à l’interface Air/MCP

---

Intérieur du MCP

Un bilan d’énergie sur un volume de contrôle du mur permet d’écrire:

$$\begin{array}{}\text{(1)}& \frac{\partial H}{\partial t}=\overrightarrow{\mathrm{\nabla }}\left({\lambda }_k\overrightarrow{\mathrm{\nabla }}T\right)\end{array}$$

En décomposant l’enthalpie volumique totale $H$ en enthalpie sensible volumique et chaleur latente volumique:

$$\begin{array}{}\text{(2)}& H(T)=h(T)+{\rho }_{L}L\cdot f\end{array}$$

• $f$ est la fraction liquide (fondue)

L’enthalpie sensible volumique a pour expression:

$$\begin{array}{}\text{(3)}& h(T)={\int }_{T_f}^T{\rho }_k\cdot c_k\cdot dT\end{array}$$

• $k$ correspond à la phase du MCP
• $T_f$ correspond à la température de fusion (et solidification) du MCP
• l’enthalpie étant définie à une constante près, ce choix de borne inférieur est arbitraire mais permet de simplifer les équations

En combinant (1), (2) et (3) on obtient:

$$\begin{array}{}\text{(4)}& \frac{\partial h}{\partial t}=\frac{\partial }{\partial x}(\alpha \cdot \frac{\partial h}{\partial x})-{\rho }_L\cdot L\cdot \frac{\partial f}{\partial t}\end{array}$$

• $\alpha =\frac{\lambda }{\rho \cdot c}$

Que l’on discrétise selon:

$$\begin{array}{}\text{(5)}& h_i^{t+1}=h_i^t+\alpha R\cdot (h_{i+1}^{t+1}-2h_i^{t+1}+h_{i-1}^{t+1})+p_{L}L\cdot (f^t-f^{t+1})\end{array}$$

Que l’on écrit (pour résoudre matriciellement) sous la forme:

$$\begin{array}{}\text{(6)}& a_{i-1}{h}_{i-1}^{t+1}+a_i{h}_i^{t+1}+a_{i+1}{h}_{i+1}^{t+1}=Q\end{array}$$

• $a_{i-1}=a_{i+1}=-\alpha R$
• $Q=h_i^t+{\rho }_{L}L\cdot (f_i^t-f_i^{t+1})$

---

Interface Solide/MCP

• Illustration de deux MCP en contact (les noeuds fantômes ne sont pas représentés)

• Les solides étant aussi des matériaux à changement de phase (simplements utilisés en phase constante) il est alors logique de s’intéresser à une interface généralle MCP/MCP

Conditions d’interface:

En traduisant la continuité du flux de chaleur et la continuité de la température à l’interface, on obtient:

$${{{\lambda }_1\cdot \frac{\partial T_1}{\partial x})}_{x_{int}}={\lambda }_2\cdot \frac{\partial T_2}{\partial x})}_{x_{int}}$$

$$T_{\text{int}}=T_1\left(x_{\text{int }}\right)=T_2\left(x_{\text{int }}\right)$$

Que l’on discrétise en:

$${\lambda }_1\cdot \frac{\overline{T_1}(N+1)-T_1(N)}{dx}={\lambda }_2\cdot \frac{T_2(1)-\overline{T_2}(0)}{dx}$$

$$T_{int}=\frac{T_1(N)+{\bar{T}}_1(N+1)}{2}=\frac{T_2(1)+{\bar{T}}_2(0)}{2}$$

• Illustration du noeud fantôme du matériau de gauche situé  « à la place » du noeud 1 du matériau de droite

• $\overline{T_1}(N+1)$ et $\overline{T_2}(0)$ sont les noeuds fantômes (seul $\overline{T_1}(N+1)$ est représenté sur l’illustration)
• Les noeuds fantômes permettent de considérer en $N$ (resp. en $1$) que le ${\text{MCP}}_1$ (resp. ${\text{MCP}}_2$) est entouré de noeuds constitués uniquement de ${\text{MCP}}_1$ (resp. ${\text{MCP}}_2$) et ainsi pouvoir discrétiser les conditions sur les flux de chaleur et les conditions sur les températures (ces conditions nécessitent des propriétés thermodynamiques uniformes).
• Ces noeuds n’existant pas, on les élimine des équations par la suite.

On résout pour les noeuds fantômes:

$$\overline{T_2}(0)=T_1(N)\cdot \left(\frac{2{\lambda }_1}{{\lambda }_1+{\lambda }_2}\right)+T_2(1)\cdot \left(\frac{{\lambda }_2-{\lambda }_1}{{\lambda }_1+{\lambda }_2}\right)$$

$$\overline{T_1}(N+1)=T_1(N)\cdot \left(\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)+T_2(1)\cdot \left(\frac{2{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)$$

Que l’on notera (pour simplifier):

$$\overline{T_2}(0)=(1-{\beta }_{1/2})\cdot T_1(N)+{\beta }_{1/2}\cdot T_2(1)$$

$$\overline{T_1}(N+1)={\beta }_{2/1}\cdot T_1(N)+(1-{\beta }_{2/1})\cdot T_2(1)$$

• ${\beta }_{j/\mu }=\frac{{\lambda }_{\mu }-{\lambda }_j}{{\lambda }_{\mu }+{\lambda }_j}$

On fait apparaître l’enthalpie sensible volumique des noeuds fantômes:

$$\overline{h_{2,0}^{t+1}}=(1-{\beta }_{1/2})\cdot \frac{{\rho }_2\cdot c_2}{{\rho }_1\cdot c_1}\cdot h_{1,N}^{t+1}+{\beta }_{1/2}\cdot h_{2,1}^{t+1}+(1-{\beta }_{1/2})\cdot (T_{f_1}-T_{f_2})\cdot {\rho }_2{c}_2$$

$$\overline{h_{1,N+1}^{t+1}}={\beta }_{2/1}\cdot h_{1,N}^{t+1}+\frac{{\rho }_1\cdot c_1}{{\rho }_2\cdot c_2}\cdot (1-{\beta }_{2/1})\cdot h_{2,1}^{t+1}+(1-{\beta }_{2/1})\cdot (T_{f_2}-T_{f_1})\cdot {\rho }_1{c}_1$$

• On s’est servi du fait que $h(T)=\rho c\cdot (T-T_{f_m})$ où $T_{f_m}$ correspond à la température de fusion du matériau (noté $m$) du noeud

Que l’on notera (pour simplifier):

$$\overline{h_{2,0}^{t+1}}=(1-{\beta }_{1/2})\cdot p_{2/1}\cdot h_{1,N}^{t+1}+{\beta }_{1/2}\cdot h_{2,1}^{t+1}+(1-{\beta }_{1/2})\cdot (T_{f_1}-T_{f_2})\cdot {\rho }_2{c}_2$$

$$\overline{h_{1,N+1}^{t+1}}={\beta }_{2/1}\cdot h_{1,N}^{t+1}+(1-{\beta }_{2/1})\cdot p_{1/2}\cdot h_{2,1}^{t+1}+(1-{\beta }_{2/1})\cdot (T_{f_2}-T_{f_1})\cdot {\rho }_1{c}_1$$

• $p_{j/\mu }=\frac{{\rho }_j{c}_j}{{\rho }_{\mu }{c}_{\mu }}$

Cas où un seul MCP est présent dans le mur

$$\overline{h_{2,0}^{t+1}}=(1-{\beta }_{1/2})\cdot p_{2/1}\cdot h_{1,N}^{t+1}+{\beta }_{1/2}\cdot h_{2,1}^{t+1}$$

$$\overline{h_{1,N+1}^{t+1}}={\beta }_{2/1}\cdot h_{1,N}^{t+1}+(1-{\beta }_{2/1})\cdot p_{1/2}\cdot h_{2,1}^{t+1}$$

• Ces formules ne sont valables que si le mur contient un seul MCP « réel » (hors les solides constants comme le béton) et où pour tout matériau $m$ présent dans le mur on a défini $h_m(T)$ comme $h_m(T)=\rho c\cdot (T-T_{f_{ref}})$
• $T_{f_{ref}}$ correspondant à la température de fusion du seul MCP « réel » du mur.

On notera qu’en créeant une séparation artificielle sur un même matériau (i.e. en considérant les paramètres thermodynamiques 1 et 2 égaux dans les équations précédentes), on a cohérence des enthalpies fantômes:

Missing or unrecognized delimiter for \left

$$
\left{\begin{array}{l}\overline{h_{2,0}^{t+1}}=h_{1, N}^{t+1} \ \overline{h_{1, N+1}^{t+1}}=h_{2,1}^{t+1}\end{array}\right.
$$

On reprend l’équation (5) traduisant les transferts, et l’on réinjecte les noeuds fantômes:

Pour le noeud de gauche (matériau 1)

$$-{\gamma }_1\cdot h_{i-1}^{t+1}+[1+{\gamma }_1(2-{\beta }_{2/1})]\cdot h_i^{t+1}-[{\gamma }_1\cdot p_{1/2}\cdot (1-{\beta }_{2/1})]\cdot h_{i+1}^{t+1}=h_i^t+{\gamma }_1\cdot (1-{\beta }_{2/1})\cdot {\left(\mathrm{\Delta }{T}_f\right)}_1^2\cdot p_1{c}_1+\eta \cdot (f_i^t-f_i^{t+1})$$

• ${\gamma }_j={\alpha }_{j}R$

Soit en utilisant la forme de (6):

• $a_{i-1}=-{\gamma }_1$
• $a_i=1+{\gamma }_1(2-{\beta }_{2/1})$
• $a_{i+1}=-{\gamma }_1\cdot p_{1/2}\cdot (1-{\beta }_{2/1})$
• $Q=h_i^t+{\gamma }_1\cdot (1-{\beta }_{2/1})\cdot {\left(\mathrm{\Delta }{T}_f\right)}_1^2\cdot p_1{c}_1+\eta \cdot (f_i^t-f_i^{t+1})$

Pour le noeud de droite (matériau 2)

$$-[{\gamma }_2\cdot p_{2/1}\cdot (1-{\beta }_{1/2})]\cdot h_{i-1}^{t+1}+[1+{\gamma }_2(2-{\beta }_{1/2})]\cdot h_i^{t+1}-{\gamma }_2\cdot h_{i+1}^{t+1}=h_i^t+{\gamma }_2\cdot (1-{\beta }_{1/2})\cdot {\left(\mathrm{\Delta }{T}_f\right)}_2^1\cdot p_2{c}_2+\eta \cdot (f_i^t-f_i^{t+1})$$

Soit en utilisant la forme de (6):

• $a_{i-1}=-{\gamma }_2\cdot p_{2/1}\cdot (1-{\beta }_{1/2})$
• $a_i=1+{\gamma }_2(2-{\beta }_{1/2})$
• $a_{i+1}=-{\gamma }_2$
• $Q=h_i^t+{\gamma }_2\cdot (1-{\beta }_{1/2})\cdot {\left(\mathrm{\Delta }{T}_f\right)}_2^1\cdot p_2{c}_2+\eta \cdot (f_i^t-f_i^{t+1})$

Interface Air/MCP

• Il y a ici deux interfaces différentes Air/MCP:
  1. Extérieur/Mur: La température exterieure est fixée
  2. Mur/Intérieur: La température de la pièce est inconnue
• Ces deux interfaces suivront chacune une loi de Newton de paramètres respectifs $h_{ext}$ et $h_{int}$

Interface Extérieur/Mur

• Illustration du noeud fantôme (hachuré)

En exprimant la continuité du flux de chaleur à l’interface ( $x=x_{int}$ ) :

$$\overrightarrow{j_{th}(x_{int})}=-\lambda \cdot {\frac{\partial T(x)}{\partial x}|}_{x=x_{int}}\cdot \overrightarrow{x}=h_{\text{ext}}\cdot (T_{\text{ext}}-T_{\text{interface}})\cdot \overrightarrow{x}$$

• $T(x)$ correspond exclusivement à la température dans le MCP

et en se servant de la méthode des noeuds fantômes (en considérant une cellule imaginaire de MCP à gauche de l’interface), tout en discrétisant, on obtient:

$$\begin{array}{}\text{(Int.1)}& -\lambda \cdot \frac{T(1)-\bar{T}(0)}{dx}=h_{ext}\cdot (T_{ext}-\frac{T(1)+\bar{T}(0)}{2})\end{array}$$

• où $T_{interface}$ est la température à la surface du mur, soit la température entre le $0^{eme}$ (fantôme) et $1^{er}$ noeud: on considère ici la moyenne des deux noeuds comme étant la température de l’interface.

En isolant $\bar{T}(0)$ :

$$\bar{T}(0)=\frac{2\lambda -h_{\text{ext }}dx}{2\lambda +h_{ext}dx}\cdot T(1)+\frac{2h_{ext}dx}{2\lambda +h_{ext}dx}\cdot T_{\text{ext }}$$

Que l’on notera (pour simplifier):

$$T(0)=\nu \cdot T(1)+(1-\nu )\cdot T_{ext}$$

• $\nu =\frac{2\lambda -h_{\text{ext }}dx}{2\lambda +h_{ext}dx}$

On fait ainsi apparaître l’enthalpie du noeud fantôme:

$$\overline{h_0}=\nu \cdot h_1+(1-\nu )\cdot \rho c\cdot (T_{ext}-T_f)$$

• $T_f$ est la température de fusion du MCP
• On rappelle que selon (3): $h(T)=\rho c\cdot (T-T_f)$

En réinjectant dans l’équation (5) traduisant les transferts:

$$h_1^{t+1}=h_1^t+\alpha R[(\nu -2)\cdot h_1^{t+1}+h_2^{t+1}+(1-\nu )\cdot \rho c\cdot (T_{ext}-T_f)]+{\rho }_{L}L(f^t-f^{t+1})$$

Que l’on met sous la forme (pour résoudre matriciellement):

$$[1+\gamma \cdot (2-\nu )]\cdot h_1^{t+1}-\gamma \cdot h_2^{t+1}=h_1^t+[\gamma \cdot (1-\nu )\cdot \rho c\cdot (T_{ext}-T_f)]+{\rho }_{L}L(f^t-f^{t+1})$$

Soit en utilisant la forme de (6):

• $a_{i-1}=0$
• $a_i=1+\gamma \cdot (2-\nu )$
• $a_{i+1}=-\gamma$
• $Q=h_1^t+[\gamma \cdot (1-\nu )\cdot \rho c\cdot (T_{ext}-T_f)]+\eta \cdot (f^t-f^{t+1})$
• $\nu =\frac{2\lambda -h_{\text{ext }}dx}{2\lambda +h_{ext}dx}$ En rappelant: $\gamma =\alpha R$ et $\eta ={\rho }_{L}L$

Interface Mur/Intérieur

• On fixe la température intérieure à $T_{room}$
• Cette température est valable loin du mur

Point de vue du dernier noeud du mur

• Illustration du noeud fantôme utilisé (hachuré)

En utilisant la même méthode que celle utilisée pour parvenir à (Int.1), on obtient en isolant $\overline{T_w}(N+1)$:

$$\overline{T_w}(N+1)=\phi \cdot T_w(N)+(1-\phi )\cdot T_{\text{room }}$$

• $\phi =\frac{2\lambda -h_{\text{int}}\cdot dx}{2\lambda +h_{\text{int}}\cdot dx}$

En faisant apparaître l’enthalpie volumique du mur:

$$\bar{h}(N+1)=\phi \cdot h(N)+(1-\phi )\cdot \rho c\cdot (T_{room}-T_f)$$

• $\rho$ et $c$ sont les paramètres thermodynamiques du mur.
• $T_f$ est la température de fusion du mur

Finalement, en réinjectant dans l’équation (5), traduisant les transferts puis en y mettant sous la forme de (6) :

• $a_{i-1}=-\gamma$
• $a_i=1+\gamma \cdot (2-\phi )$
• $a_{i+1}=0$
• $Q=h_i^t+\gamma \cdot (1-\phi )\cdot \rho c\cdot (T_{room}-T_f)+{\rho }_{L}L\cdot (f^t-f^{t+1})$

---

---

Résolution Numérique

Matrice globale

Le schéma numérique utilisé est ici implicite. Sa mise sous forme matricelle se fait en considérant un vecteur contenant les enthalpies volumiques de chaque noeud (de la gauche du mur jusqu’à sa droite) au temps $t$:

$$\begin{array}{}\text{(V.1)}& H^t=\left(\begin{array}{c}{h}_1^t\\ ⋮\\ h_N^t\end{array}\right)\end{array}$$

De même pour les fractions liquides:

$$\begin{array}{}\text{(V.2)}& F_k^t=\left(\begin{array}{c}{f}_{1,k}^t\\ ⋮\\ f_{N,k}^t\end{array}\right)\end{array}$$

• $k$ est défini en détail ici

Pour passer à $t+dt$, il convient alors de résoudre:

$$\left(\begin{array}{cccccc}{a}_1^1& a_2^1& 0& \dots & \dots & 0\\ a_1^2& a_2^2& a_3^2& 0& \dots & 0\\ 0& \ddots & \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & \ddots & 0\\ 0& \dots & 0& a_{N-2}^{N-1}& a_{N-1}^{N-1}& a_N^{N-1}\\ 0& \dots & \dots & 0& a_{N-1}^N& a_N^N\end{array}\right)\cdot \left(\begin{array}{c}{h}_1^{t+dt}\\ ⋮\\ ⋮\\ ⋮\\ ⋮\\ h_N^{t+dt}\end{array}\right)=\left(\begin{array}{c}{h}_1^t\\ ⋮\\ ⋮\\ ⋮\\ ⋮\\ h_N^t\end{array}\right)+\eta \cdot \left(\begin{array}{c}{f}_1^t-f_{1,k}^{t+dt}\\ ⋮\\ ⋮\\ ⋮\\ ⋮\\ f_N^t-f_{N,k}^{t+dt}\end{array}\right)+E$$

• $a_{i-1}^j$, $a_i^j$ et $a_{i+1}^j$ correspondent aux coefficients trouvés dans les parties précédentes pour un noeud $j$
• Les lignes correspondant à un noeud « solide constant » dans le vecteur des différences de fractions liquides seront nulles: étant donné que le matériau ne change pas de phase.
• $E$ correspond aux termes supplémentaires relatifs aux bords/interfaces

Il convient donc de résoudre le système:

$$A\cdot H^{t+dt}=H^t+\eta \cdot {\left(\mathrm{\Delta }{F}_k\right)}_{t+dt}^t+E$$

ou:

$$A\cdot H^{t+dt}=B$$

• $B=H^t+\eta \cdot {\left(\mathrm{\Delta }{F}_k\right)}_{t+dt}^t+E$
• $A$ est une matrice tridiagonale
• Les solutions de ce système peuvent être obtenues grâce à l’algorithme de Thomas

Itérations internes: problème d’inconnues

• Le nouveau terme de fraction liquide étant aussi une inconnue, on ne peut résoudre ce système  « d’un seul coup »: à chaque pas de temps, il conviendra donc de trouver le nouveau vecteur fraction liquide

En reprenant l’équation « de base », pour un pas de temps quelconque fixé (on n’affiche pas $t+dt$, on met simplement $old$ en exposant pour repérer les anciennes valeurs):

$$\begin{array}{}\text{(R.1)}& a_W{h}_W+a_P{h}_P+a_E{h}_E=h_P^{old}+\rho L{f}^{old}-\rho L{f}_k\end{array}$$

• $a_W\equiv a_{i-1}$
• $a_P\equiv a_i$
• $a_E\equiv a_{i+1}$

A chaque itération (dans un seul pas de temps), on applique un solveur TDMA à cette équation (où $f_k$ correspond à la $k^{eme}$ évaluation de la fraction liquide au nœud P). On met ensuite à jour le champ de fraction liquide (i.e. le tableau, vecteur entier des fractions liquides). Cette mise à jour est cruciale dans cette méthode. Après la 1ère itération, on a :

$$\begin{array}{}\text{(R.2)}& a_P{h}_P=-a_E{h}_E-a_W{h}_W+h_P^{old}+\rho L{f}^{old}-\rho L{f}_0\end{array}$$

Donc, après la $(k+1{)}^{eme}$ itération, on a :

$$\begin{array}{}\text{(R.3)}& a_P{h}_P=-a_E{h}_E-a_W{h}_W+h_P^{old}+\rho L{f}^{old}-\rho L{f}_k\end{array}$$

Si un changement de phase se passe au $P^{eme}$ nœud (i.e. $0<f_k<1$ ), alors la $k^{eme}$ estimation de la fraction liquide — i.e. $f_k$— doit être mise à jour de sorte que pour la $(k+2{)}^{eme}$ itération, la partie gauche de (R.3) soit égale à zéro — grâce au nouveau $f_{k+1}$ — c’est-à-dire :

$$\begin{array}{}\text{(R.4)}& 0=-a_E{h}_E-a_W{h}_W+h_P^{old}+\rho L{f}^{old}-\rho L{f}_k+update\end{array}$$

On a donc :

$$update=-a_P{h}_P$$

L’équation étant utilisée pour la $(k+2{)}^{eme}$ itération étant :

$$a_P{h}_P=-a_E{h}_E-a_W{h}_W+h_P^{old}+\rho L{f}^{old}-\rho L{f}_{k+1}$$

Il vient alors :

$$-\rho L{f}_k+update=-\rho L{f}_{k+1}$$

Puis :

$$f_{k+1}=f_k+\frac{a_P{h}_P}{\rho L}$$

Que l’on peut modifier en :

$$\begin{array}{}\text{(R.5)}& f_{k+1}=f_k+\lambda \frac{a_P{h}_P}{\rho L}\end{array}$$

Où $\lambda$ est un coefficient de sous-relaxation qui permet d’atteindre la convergence.

En pratique, après la $k^{eme}$ solution du TDMA, on applique cette mise à jour à chaque nœud (pas seulement aux nœuds en changement de phase). Comme cette mise à jour n’est pas adaptée à tous les nœuds, on la suit d’une correction de dépassement/sous-dépassement:

Missing or unrecognized delimiter for \left

$$
f=\left{\begin{array}{ll}
0 & \text { si } f_{k+1}<0 \\
1 & \text { si } f_{k+1}>1
\end{array}\right.
\tag{R.6}
$$

• Cette correction a deux avantages :
• 1. Il n’y a pas besoin de vérifier où et quand appliquer la correction
• 2. Il y a une totale et correcte prise en charge des situations quand le front passe d’un nœud à un autre.
• Le secret de cette méthode réside dans la mise à jour de la fraction liquide depuis le vecteur d’enthalpie sensible : (R.5) remplit ce rôle.

Optimisation

Ici, on introduit une modification qui permettra des calculs plus rapides. En effet, on n’utilisait pas une information potentiellement importante : si la fraction liquide au nœud $P$ est strictement dans l’intervalle $]0,1[$ alors, $h_P=0$, (selon la définition de l’enthalpie (3)). Cette information peut être forcée sur le solveur TDMA en mettant simplement le coefficient $a_P=BIG\left({10}^{15}\right)$ à chaque fois que $0<f_k<1$ pour le nœud en question. De cette manière, le solveur TDMA retournera une valeur pour ${\left(h_P\right)}_{k+1}$ proche de zéro. En mettant par la suite $h_P=0$ on a la nouvelle mise à jour suivante:

$$\begin{array}{}\text{(R.7)}& f_{k+1}=\frac{-a_W{h}_W-a_E{h}_E+h_P^{old}}{\rho L}+f^{old}\end{array}$$

Qui ne nécessite pas de coefficient de relaxation. Le nouveau critère de convergence sera :

$$\begin{array}{}\text{(R.8)}& \frac{\sum ABS\left({RES}_P\right)}{c_P}<TOL\end{array}$$

• ${RES}_P=a_W{h}_w+a_P{h}_P+a_E{h}_E-h_P^{old}-\rho L{f}^{old}+\rho L{f}_k$

---

Fonctionnement du programme Python

Librairies/Modules utilisés

• numpy
• pathlib
• matplotlib
• math

Configuration de l'expérience

Cette partie se passe exclusivement dans le dossier Config (et Weather_Data si la température extérieure varie selon des données pré-enregistrées)

1. Ajouter des matériaux dans le fichier materials_config.csv (ces matériaux n'ont pas besoin d'être utilisés par la suite)
2. Configurer le mur dans le fichier wall_config.csv:

• chaque ligne correspond à une épaisseur de matériau (la dernière ligne correspondra à la couche la plus à droite du mur)
• le nom du matériau d'une couche doit correspondre à un matériau dans materials_config.csv
• l'épaisseur (en $m$) doit être indiquée sur la colonne de droite pour chaque épaisseur de matériau

3. Configurer certaines données de l'expérience dans le fichier experiment_config.ini (se référer aux commentaires présents)
4. Modifier la loi de température extérieure (sinon utiliser température pré-enregistrée) dans temperature_config.py, e.g. si la température extérieure doit être constante:

def update_outside_temperature(t: float) -> float:
    pass

Dans le fichier main.py, modifier l'appel de Experiment de sorte à ce qu'il n'y ait que les 3 arguments suivants (contrairement au cas d'une température pré-enregistrée):

E = Experiment(str((current_path / 'Config' / 'experiment_config.ini').resolve()),
             str((current_path / 'Config' / 'wall_config.csv').resolve()),
             str((current_path / 'Config' / 'materials_config.csv').resolve()))

5. Pour utiliser des données de température externes: Utiliser un fichier CSV sous la forme:

datetime,temperature
YYYY-MM-DDTHH:MM:SS,14.1
YYYY-MM-DDTHH:MM:SS,14.5
YYYY-MM-DDTHH:MM:SS,15.0

Et le placer dans le dossier Weather_Data Dans le fichier main.py, modifier l'appel de Experiment:

E = Experiment(str((current_path / 'Config' / 'experiment_config.ini').resolve()),
             str((current_path / 'Config' / 'wall_config.csv').resolve()),
             str((current_path / 'Config' / 'materials_config.csv').resolve()),
             str((current_path / 'Weather_Data' / 'NOM_DU_FICHIER_DATA.csv').resolve()))

Simulation

Lancer main.py, une barre de chargement indiquant l'avancée du calcul devrait apparaître dans la console. Une fois terminé, une fenêtre matplotlib affiche les résultats de l'expérience. Pour supprimer le darkmode, accéder à Plot\standard_plot.py puis supprimer la première ligne de la première fonction:

def plot_simulation(simulation: Simulation):
    plt.style.use('dark_background')

Résultats

La fenêtre matplotlib montre 3 graphes:

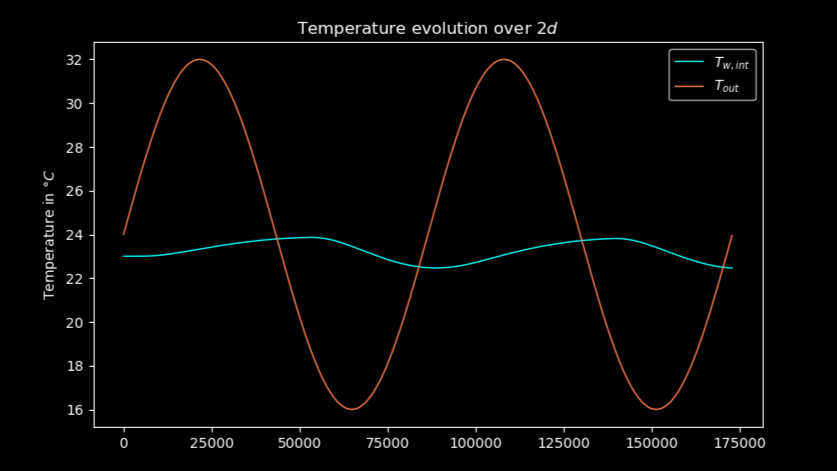
1. Température à l'extérieure et Température sur le dernier noeud du mur (en $°C$) en fonction du temps (en secondes)

• 

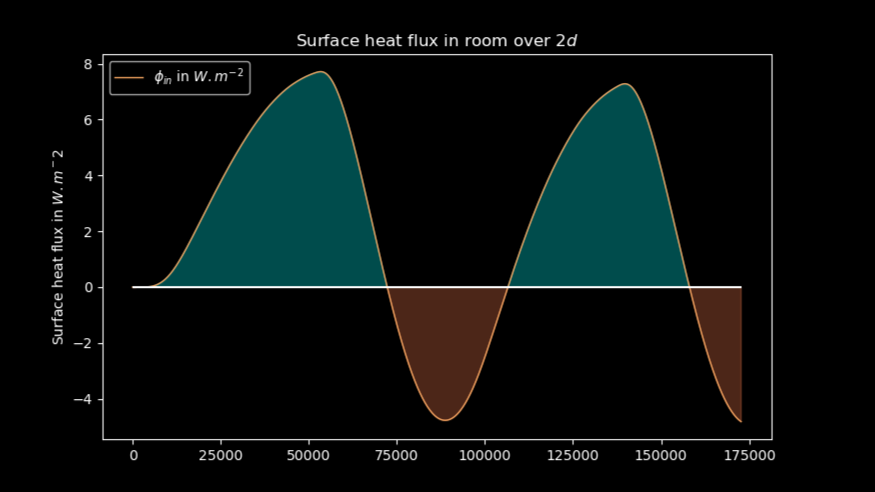
2. Flux surfacique de chaleur reçu algébriquement par la pièce (en $W.m^{-2}$) par le mur en fonction du temps: un flux positif signifie qu'une climatisation a été utilisée pour maintenir la pièce à la même température, un flux négatif signifie qu'un radiateur a été utilisé.

• 

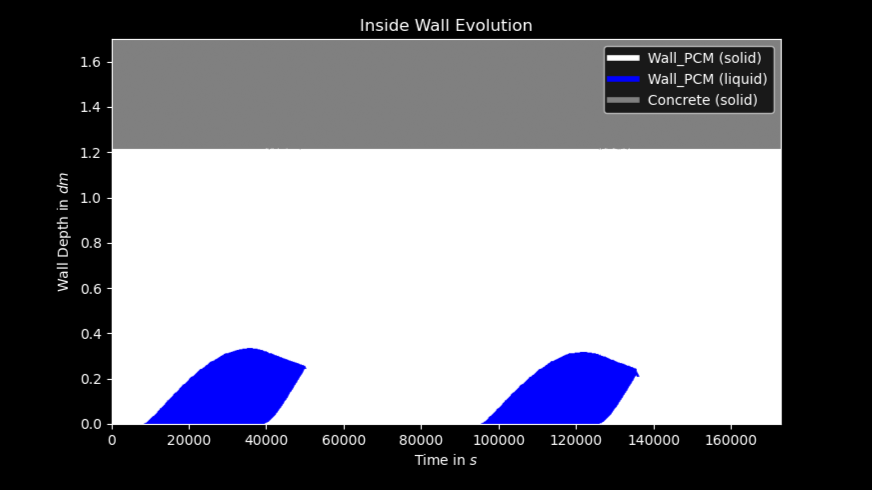
3. Évolution spatiale de(s) frontière(s) solide/liquide en fonction du temps (en secondes): en ordonnée correspond la distribution des matériaux avec leurs phases.

•