cs-implementing-a-hashtable-lab

Learning goals

1. Implement the Map interface using a hash table.
2. Analyze the performance of the hash table implementation.
3. Identify and fix performance bugs.

Overview

In this lab, you will finish off the implementation of MyBetterMap. In the previous README, we showed that the core methods of MyBetterMap are faster than MyLinearMap, but they are still linear. We'll see how to to solve that problem by allowing the hash table to grow, which you will implement in MyHashMap. Then we will profile the performance of MyHashMap and the HashMap provided by Java.

Finishing MyBetterMap

When you check out the repository for this lab, you should find a file structure similar to what you saw in previous labs. The top level directory contains CONTRIBUTING.md, LICENSE.md, README.md, and the directory with the code for this lab, javacs-lab08.

In the subdirectory javacs-lab08/src/com/flatironschool/javacs you'll find the source files for this lab:

• MyLinearMap.java contains our solution to the previous lab, which we will build on in this lab.

• MyBetterMap.java contains the code from the previous README with some methods you will fill in.

• MyHashMap.java contains the outline of a hash table that grows when needed, which you will complete.

• MyLinearMapTest.java contains the unit tests for MyLinearMap.

• MyBetterMapTest.java contains the unit tests for MyBetterMap.

• MyHashMapTest.java contains the unit tests for MyHashMap.

• Profiler.java contains code for measuring and plotting runtime versus problem size.

• ProfileMapPut.java contains code that profiles the Map.put method.

Also, in javacs-lab08, you'll find the Ant build file build.xml.

• In javacs-lab08, run ant build to compile the source files. Then run ant test1, which runs MyBetterMapTest. Several tests should fail, because you have some work to do!

• Review the implementation of put and get from the previous README. Then fill in the body of containsKey. Hint: use chooseMap. Run ant test1 again and confirm that testContainsKey passes.

• Fill in the body of containsValue. Hint: don't use chooseMap. Run ant test1 again and confirm that testContainsValue passes. Notice that we have to do more work to find a value than to find a key.

Like put and get, this implementation of containsKey is linear, because it has to search one of the embedded sub-maps. If there are n entries and k sub-maps, the size of the sub-maps is n/k on average, which is still proportional to n.

But if we increase k along with n, we can limit the size of n/k. For example, suppose we double k every time n exceeds k; in that case the number of entries per map would be less than 1 on average, and pretty much always less than 10, as long as the hash function spreads out the keys reasonably well.

If the number of entries per sub-map is constant, we can search a single sub-map in constant time. And computing the hash function is generally constant time (it might depend on the size of the key, but does not depend on the number of keys). So we might be able to make put and get constant time.

We'll see how that works in the next section.

Implementing MyHashMap

In MyHashMap.java, we provide the outline of a hash table that grows when needed. Here's the beginning of the definition:

public class MyHashMap<K, V> extends MyBetterMap<K, V> implements Map<K, V> {

	// average number of entries per sub-map before we rehash
	private static final double FACTOR = 1.0;

	@Override
	public V put(K key, V value) {
		V oldValue = super.put(key, value);

		// check if the number of elements per sub-map exceeds the threshold
		if (size() > maps.size() * FACTOR) {
			rehash();
		}
		return oldValue;
	}
}

MyHashMap extends MyBetterMap, so it inherits the methods defined there. The only method it overrides is put which calls put in the superclass — that is, it calls the version of put in MyBetterMap — and then it checks whether it has to rehash. Calling size returns the total number of entries, n. Calling maps.size returns the number of embedded maps, k.

The constant FACTOR, which is called the load factor, determines the maximum number of entries per sub-map, on average. If n > k * FACTOR, that means n/k > FACTOR, which means the number of entries per sub-map exceeds the threshold, so we call rehash.

• In javacs-lab08, run ant build to compile the source files. Then run ant test2, which runs MyHashMapTest. It should fail because our implementation of rehash throws an exception. Your job is to fill it in.

Fill in the body of rehash to collect the entries in the table, resize the table, and then put the entries back in. We provide two methods that might come in handy: MyBetterMap.makeMaps and MyLinearMap.getEntries. Your solution should double the number of maps, k, each time it is called.

Analyzing MyHashMap

If the number of entries per sub-map, n/k, is constant, several of the core MyBetterMap methods become constant time:

	public boolean containsKey(Object target) {
		MyLinearMap<K, V> map = chooseMap(target);
		return map.containsKey(target);
	}

	public V get(Object key) {
		MyLinearMap<K, V> map = chooseMap(key);
		return map.get(key);
	}

	public V remove(Object key) {
		MyLinearMap<K, V> map = chooseMap(key);
		return map.remove(key);
	}

Each method hashes a key, which is constant time, and then invokes a method on a sub-map, which is constant time.

So far, so good. But the other core method, put, is a little harder to analyze. When we don't have to rehash, it is constant time, but when we do, it's linear. In that way, it's similar to ArrayList.add, and for the same reason, it turns out to be constant time if we average over a series of put operations. Again, the argument is based on amortized analysis.

Suppose the initial number of sub-maps, k, is 2, and the load factor is 1. Now let's see how much work it takes to put a series of keys. As the basic "unit of work," we'll count the number of times we have to hash a key and add it to a sub-map.

The first time we call put it takes 1 unit of work. The second time also takes 1 unit. The third time we have to rehash, so it takes 2 units to rehash the existing keys and 1 unit to hash the new key.

Now the size of the hash table is 4, so the next time we call put, it takes 1 unit of work. But the next time we have to rehash, which takes 4 units to rehash the existing keys and 1 unit to hash the new key.

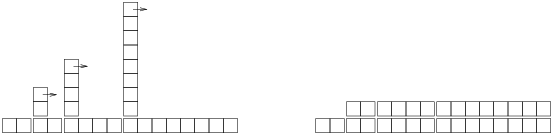
The following figure shows the pattern, with the normal work of hashing a new key shown across the bottom and extra work of rehashing shown as a tower.

As the arrows suggest, if we knock down the towers, each one fills the space before the next tower. The result is a uniform height of 2 units, which shows that the average work per put is about 2 units. And that means that put is constant time on average.

This diagram also shows why it is important to double the number of sub-maps, k, when we rehash. If we only add to k instead of multiplying, the towers would be too close together and (eventually) they would start piling up. And that would not be constant time.

The tradeoffs

We've shown that containsKey, get, and remove are constant time, and put is constant time on average. We should take a minute to appreciate how remarkable that is. The performance of these operations is pretty much the same no matter how big the hash table is. Well, sort of.

Remember that our analysis is based on a simple model of computation where each "unit of work" takes the same amount of time. Real computers are more complicated than that. In particular, they are usually fastest when working with data structures small enough to fit in cache; somewhat slower if the structure doesn't fit in cache but still fits in memory; and much slower if the structure doesn't fit in memory.

Another limitation of this implementation is that hashing doesn't help if we want to look up a value: containsValue is still linear because it has to search all of the sub-maps. And there is no particularly efficient way to look up a value and find the corresponding key (or possibly keys).

And there's one more limitation: some of the methods that were constant time in MyLinearMap have become linear. For example:

	public void clear() {
		for (int i=0; i<maps.size(); i++) {
			maps.get(i).clear();
		}
	}

clear has to clear all of the sub-maps, and the number of sub-maps is proportional to n, so it's linear. Fortunately, this operation is not used very often, so for most applications this tradeoff is acceptable.

Profiling MyHashMap

Before we go on, we should check whether MyHashMap is really constant time.

• In javacs-lab08, run ant build to compile the source files. Then run ant ProfileMapPut. It measures the runtime of HashMap.put (provided by Java) with a range of problem sizes and plots runtime versus problem size on a log-log scale. If this operation is constant time, the total time for n operations should be linear, so the result should be a straight line with slope 1. When we ran this code, the estimated slope was close to 1, which is consistent with our analysis. You should get something similar.

• Modify ProfileMapPut.java so it profiles your implementation, MyHashMap, instead of Java's HashMap. Run the profiler again and see if the slope is near 1. You might have to adjust startN and endMillis to find a range of problem sizes where the runtimes are more than a few milliseconds, but not more than a few thousand.

• When we ran this code, we got a surprise: the slope was about 1.7, which suggests that our implementation is not constant time after all. It contains a "performance bug." As the last exercise for this lab, you should track down the error, fix it, and confirm that put is constant time, as expected.

Resources

• Amortized analysis: Wikipedia.