-
Notifications
You must be signed in to change notification settings - Fork 57
Preprocessing
Preprocessing of IBI time series data is frequently required before HRV analysis to reduce analysis errors. The three primary types of IBI preprocessing are ectopic beat/interval correction, detrending, and IBI resampling. HRV analysis errors due to ectopic beats and IBI trends have been reported by Thuraisingham [5] and Colak [6]. In the context of IBI, ectopic beats refer to any IBI based on one or more abnormal beats. Any abnormal IBI that is due to either a false/missed beat, fiducial point misalignment, or cardiac ectopy may be considered ectopic.
IBI time series also contain slowly varying trends that are generally assumed to be inherent to most biological signals including IBI. Some HRV analysis methods assume that IBI signals are stationary or absent of low frequency trends. Specifically, power spectrum estimations based on Fourier transform require that the random variable of interest be wide sense stationary (the mean does not change with time) [7]. To alleviate any non-stationarities within IBI time series, detrending is often used before HRV analysis [6, 8, 9]. In addition to stationarity, these methods require evenly sampled IBI, which is inherently not the case for IBI signals. Figure 2.2 illustrates an IBI time series before and after removing both ectopic intervals and low frequency trend.
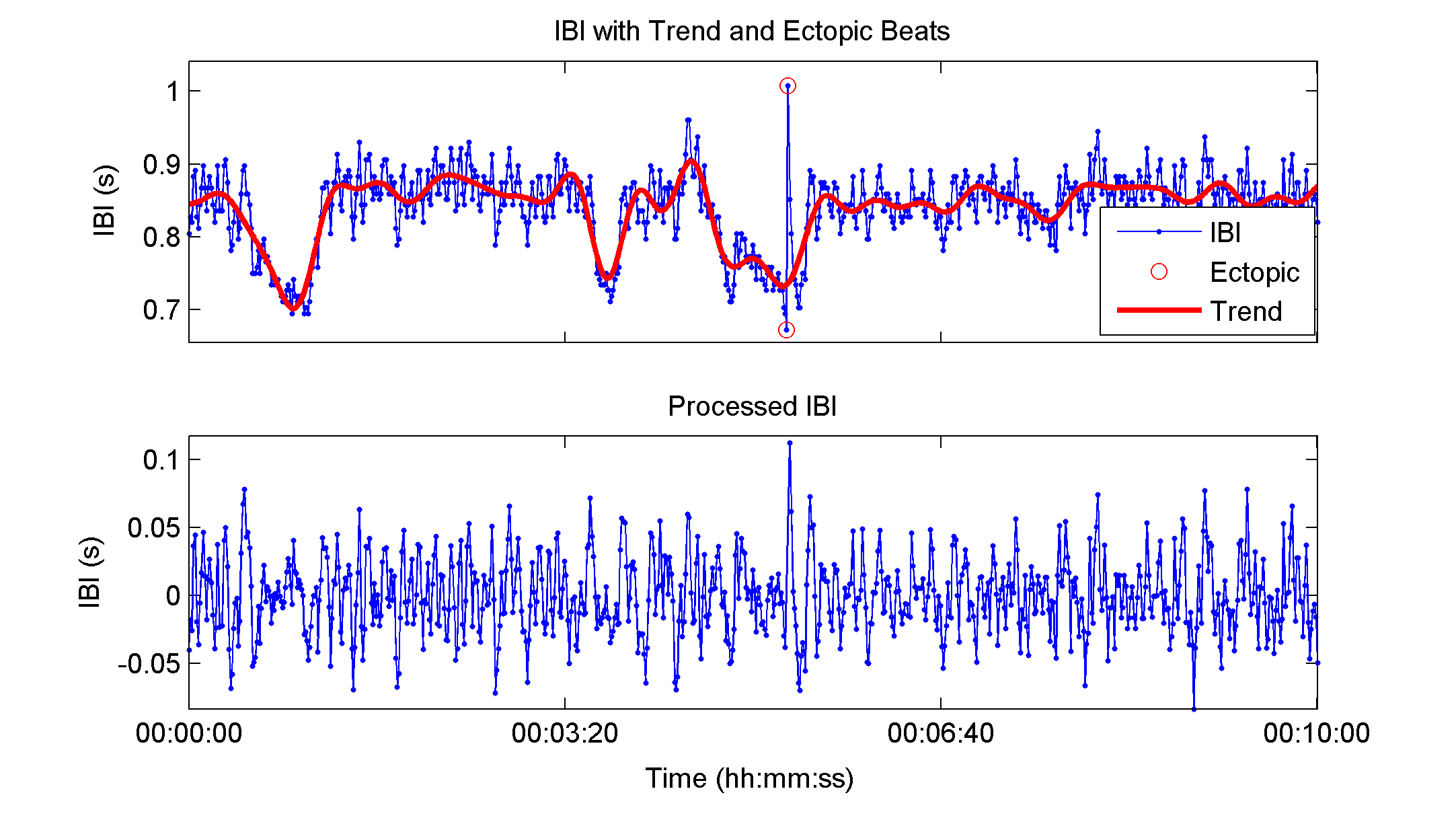
Figure 2.2 – IBI signal before and after detrending and ectopic interval removal. IBI time series from healthy human.
Before ectopic intervals can be corrected they must first be detected or marked. Here three detection techniques are discussed. Although the term filter is used in this section, no change to the original IBI occurs during ectopic interval detection. The percentage filter locates intervals that change by more than a user defined percentage (often 20%) from the previous interval [10]. This method locates any sudden or abrupt IBI changes. Another method used to detect ectopic intervals is the standard deviation filter which marks outliers as being intervals that lie beyond the overall mean IBI by a user defined value of standard deviations (often 3 SD) [10]. Lastly, the median filter acts as an impulse rejection filter with threshold to delineate ectopic intervals [5]. The median filter of a random variable x of length N using a threshold of τ is given by
Equation 2.2
Four correction techniques are described to replace ectopic intervals found during the detection process. The first technique is to simply remove any ectopic intervals found. Simple ectopic interval removal has been shown to be as effective as other replacement methods [11]. Another method replaces any ectopic interval with the mean value of w neighboring IBI intervals centered on the ectopic interval using Equation(2.3) . Similarly, the median method replaces ectopic intervals with the median value of w neighboring IBI intervals centered on the ectopic interval using Equation (2.4) [5]. Lastly, cubic spline replacement replaces ectopic intervals using cubic spline interpolation.
Equation: (2.3)
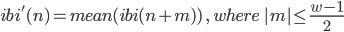
Equation (2.4)
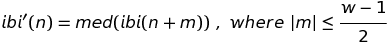
Several methods of detrending exist in the literature to remove low frequency trends including: linear detrending, polynomial detrending, wavelet detrending, wavelet packet detrending, and smoothing priors detrending.
Two of the simplest methods used for detrending IBI series are linear and polynomial detrending [12-14]. Linear detrending is accomplished by removing a linear least-squares-fit from the IBI series. Similarly, polynomial detrending removes a second or third order polynomial fit (in a least squares sense) from the IBI series.
Wavelet detrending is accomplished by decomposing the original IBI time series into a tree of approximation and detail coefficients using discrete wavelet transform (DWT) (see Section 2.5.2.2). Each decomposed sub-band is associated with a range of frequencies with the highest level of approximation containing the lowest frequencies. Removing the low frequency trend can be accomplished by two methods. The first method sets all the wavelet coefficients of the highest level approximation (lowest frequency) to zero, and then performs an inverse DWT. The alternative method reconstructs only the highest approximation sub-band which is then subtracted from the original IBI series [5]. Either method effectively applies signal detrending.
Detrending using wavelet packets works similar to the detrending method based on DWT mentioned in the previous section. Instead of decomposing the signal using DWT the discrete wavelet packet transform (DWPT) is used (see Section 2.5.2.2). Wavelet coefficients of sub-bands that contain frequency components of any unwanted trend are set to zero. Reconstruction of the IBI series using inverse DWPT produces a detrended IBI series [15].
The final detrending method to be discussed is the smoothing priors approach [15, 16]. In the smoothing priors approach a N-1 long, an equally sampled IBI time series is represented as the combination of stationary and trend components, z=zstationary + ztrend . This method computes a stationary signal from the original. The estimated stationary component is written as
Equation (2.4)
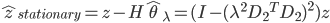
where HER(N-1)xM is the observation matrix. For simplification, an identity matrix is used in place of the observation matrix H. thetalambda represents the estimate of the regression parameters with lambda as the regularization parameter and eqn is the second order difference matrix.
In addition to most Fourier based power spectrum estimates (see Chapter 2.4) requiring signal stationarity; they also require time series that are regularly sampled in time. Spectrum estimates taken from irregularly time sampled signals can introduce additional harmonics into the power spectrum [17]. For this reason, IBI time series must be resampled prior to some power spectrum estimates. Commonly used resampling schemes are cubic spline and linear interpolation [18].
- update image numbers and their refs
- update lit references
- Fix all equations
- Add cross refs to other pages
Equations in Github links