This repository contains statistical regression utilities written in C# in Visual Studio 2019. The utilities include standard least-squares linear, quadratic, cubic, and elliptical regression. In addition to standard least squares regression, they contain "consensus regression" that automatically detects outliers in a dataset, removes them from the inliers, and updates the least-squares regression model quickly.

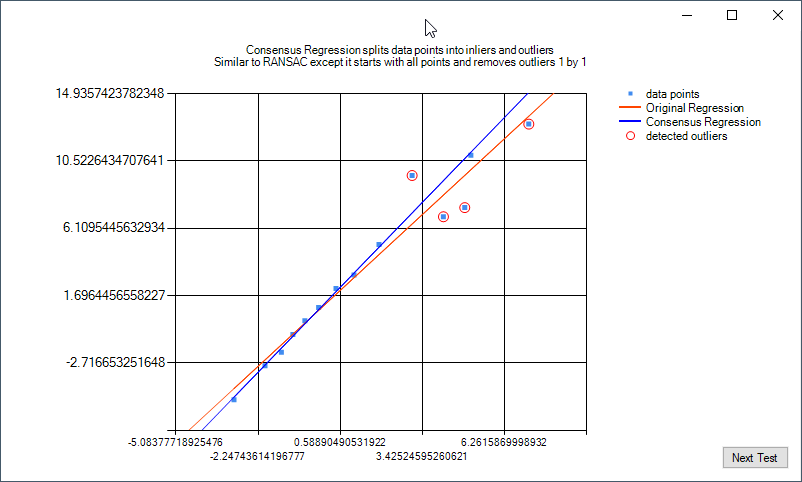
The image below is an example of linear regression and linear regression consensus. The red line is a linear regression on all data points (blue). The consensus algorithm identifies outliers (red) and then adjusts the regression model accordingly.

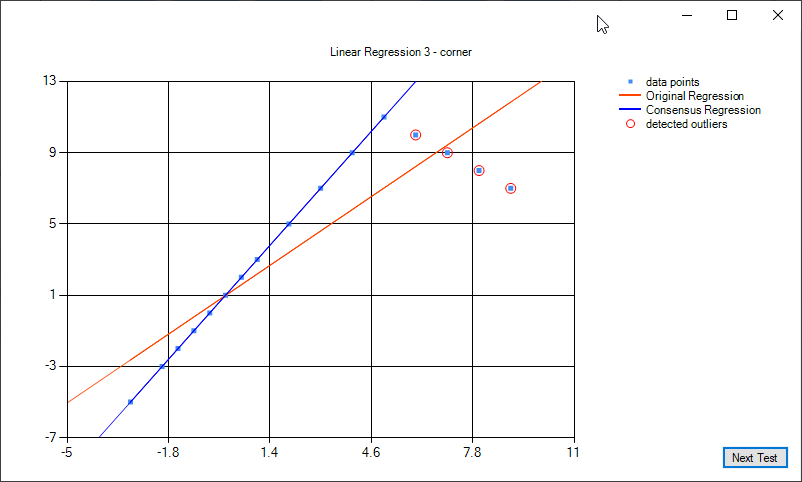
Here is an example that may apply to edge points detected in an image at a corner. The original regression (red) fits a line through both lines. The consensus algorithm identifies outliers (red) and fits its model to the dominant line.

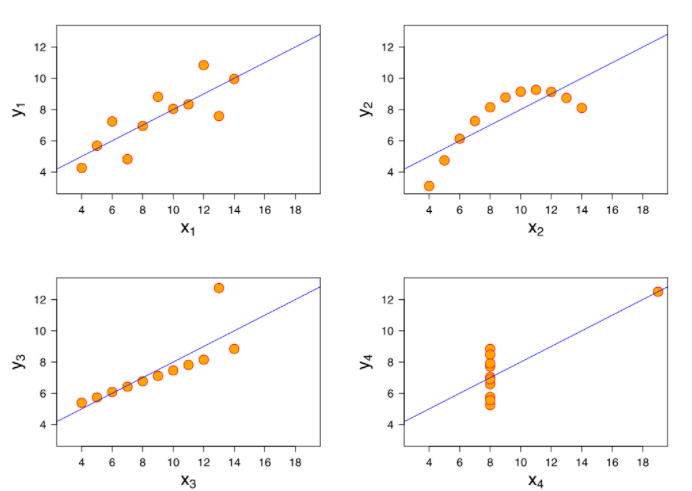
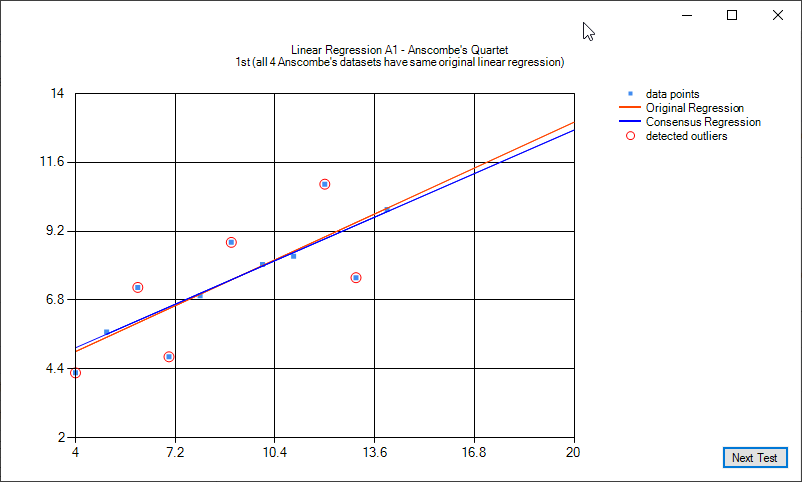
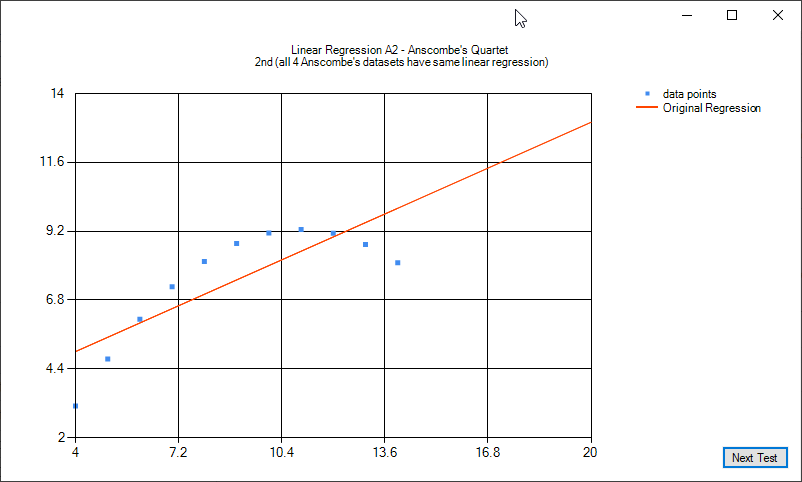
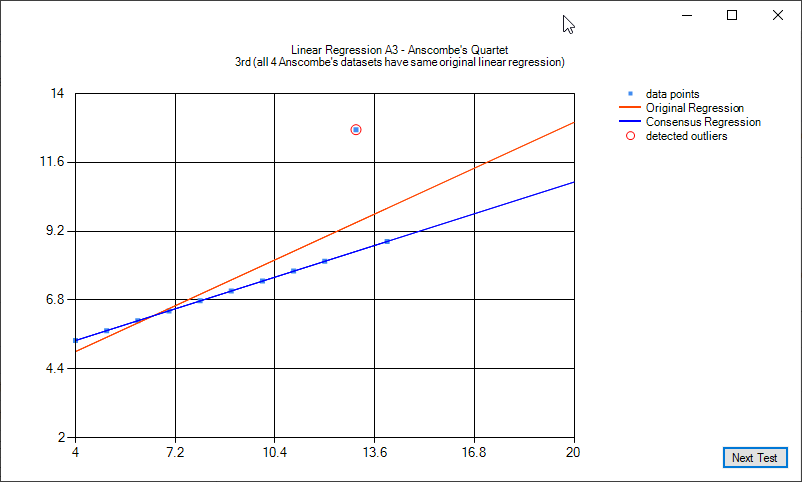
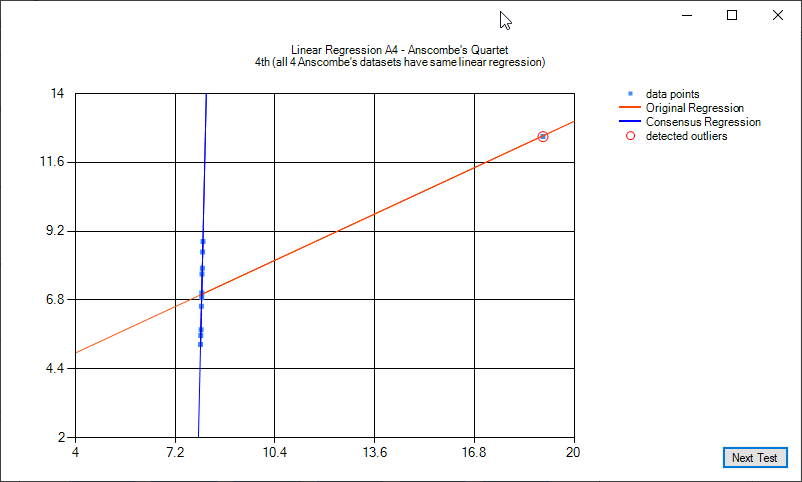
Anscombe's quartet is four sets of data that have virtually the same linear regression function. In 3 of the 4 cases, outliers have a noticeable impact. Two of the cases, a single outlier is enough to make the linear regression of poorer to unusable quality. This quartet helps demonstate the sensitivity of common regression tools to outliers. For more reading see https://en.wikipedia.org/wiki/Anscombe%27s_quartet.

The following images illustrate linear regression on the Anscombe's quartet:

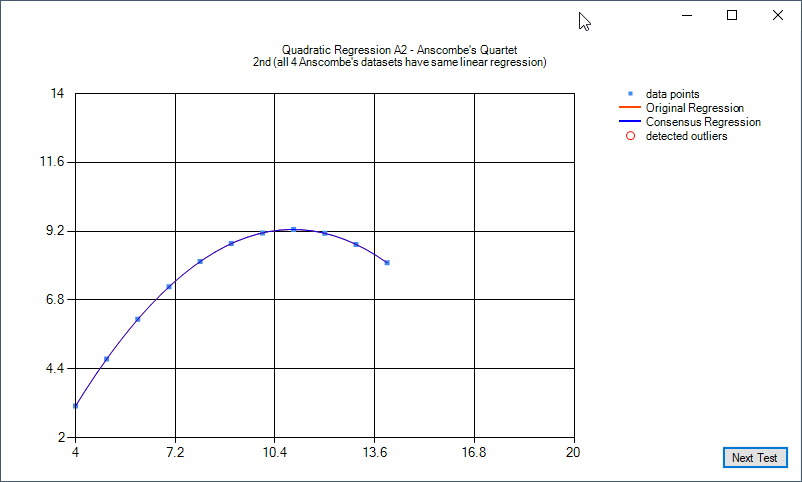
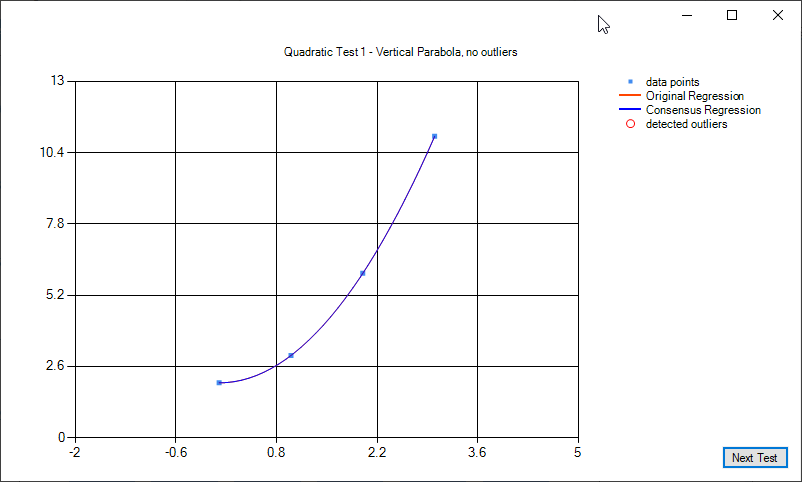
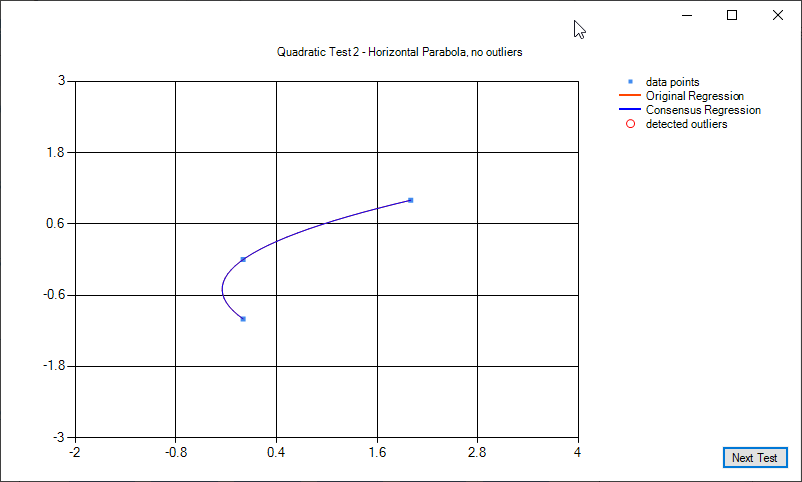
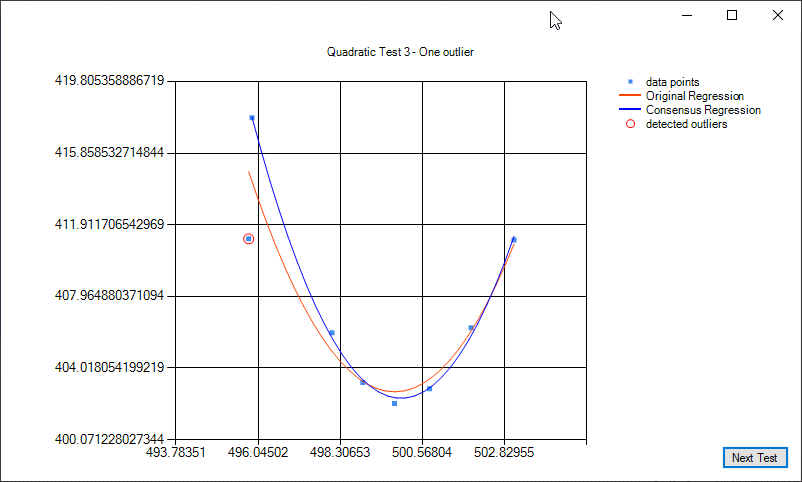
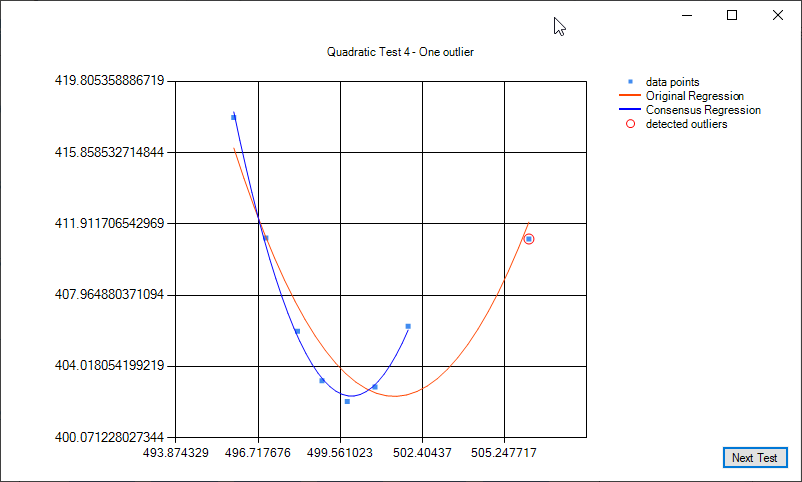
Some examples of quadratic regression and quadratic regression consensus:

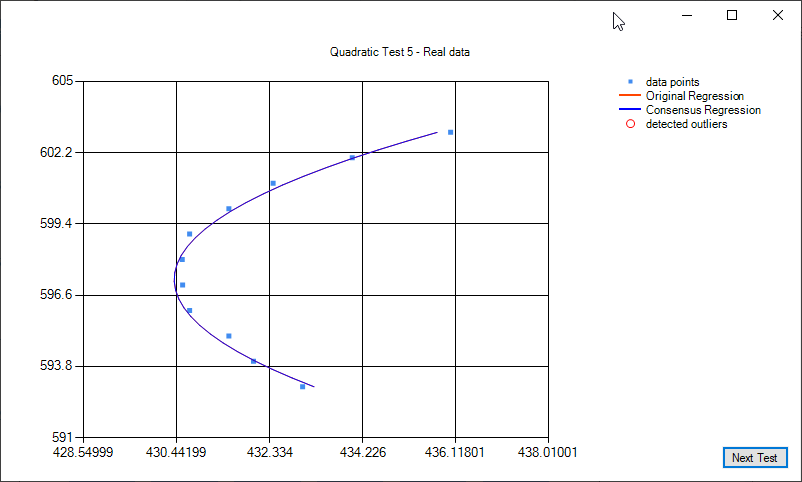
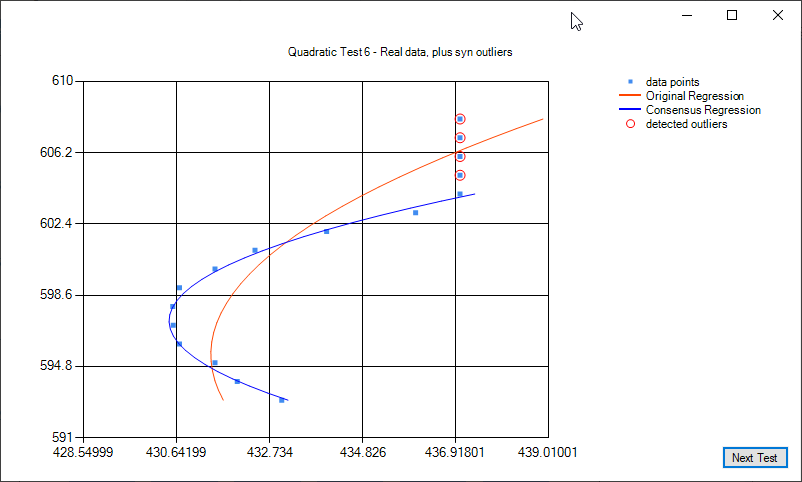
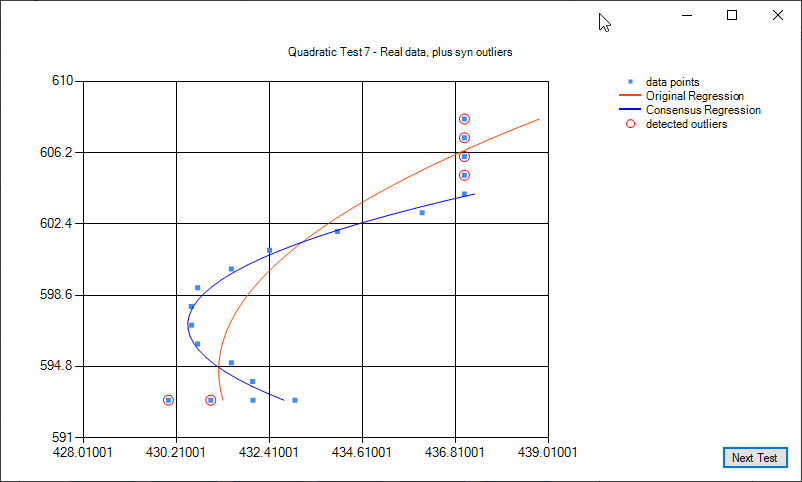
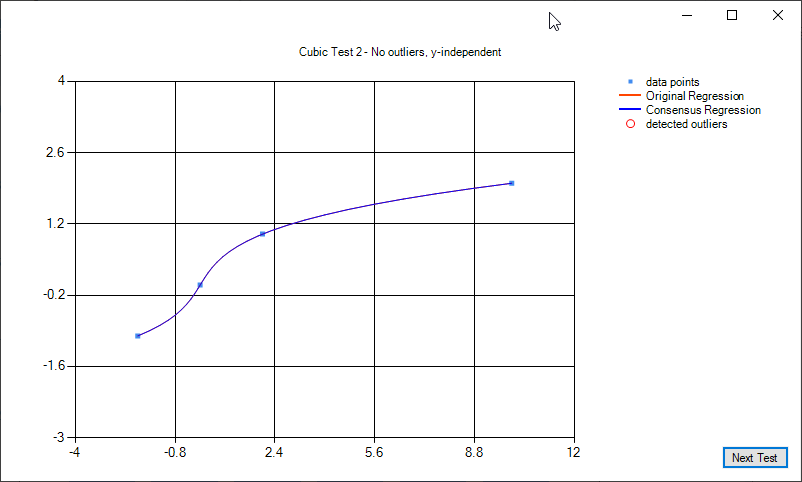
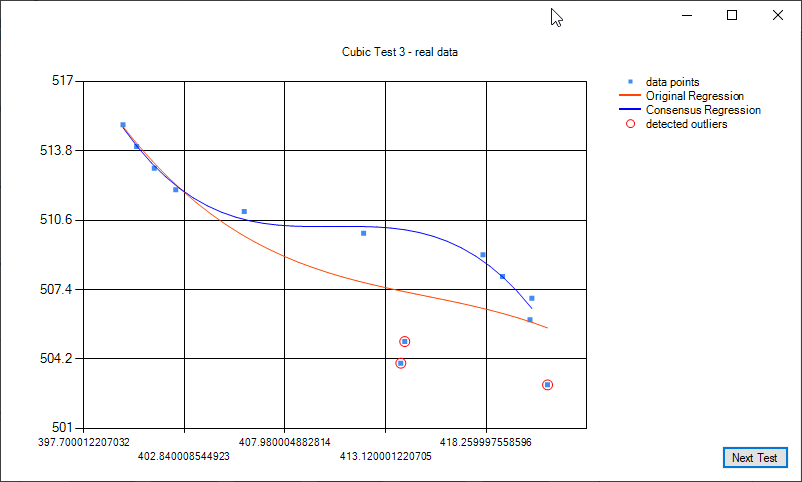
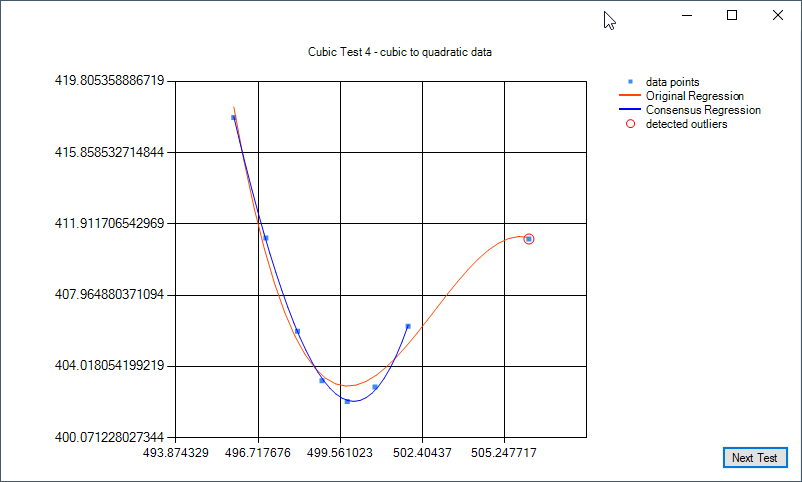
Some examples of cubic regression and cubic regression consensus:

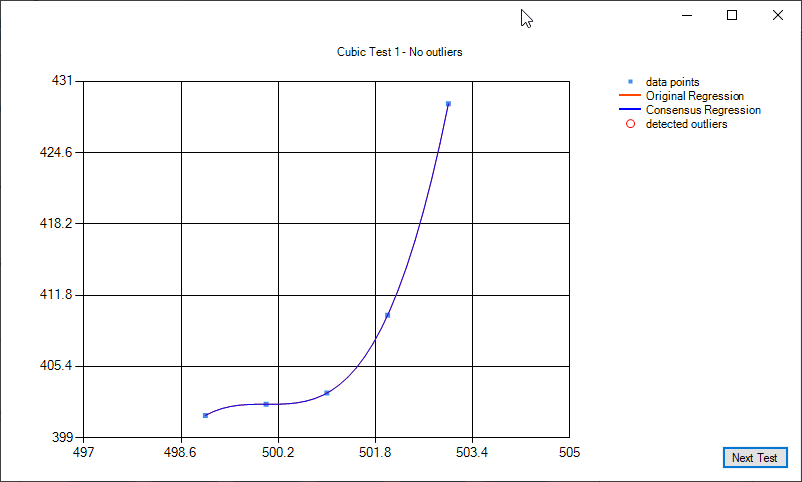
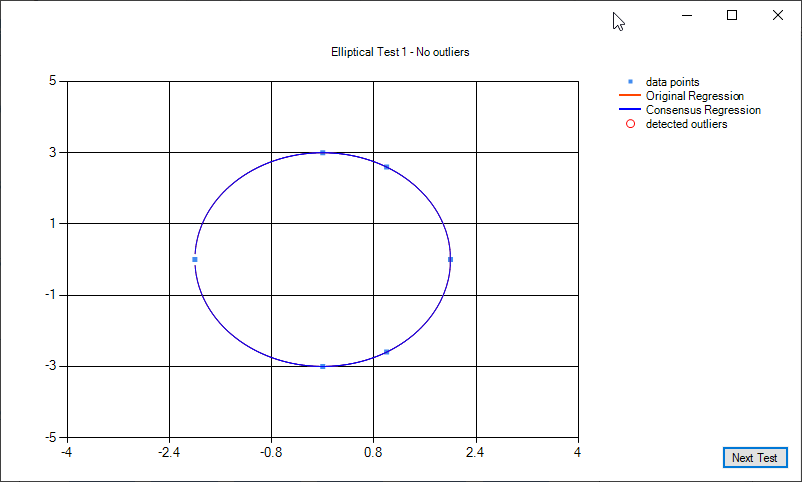
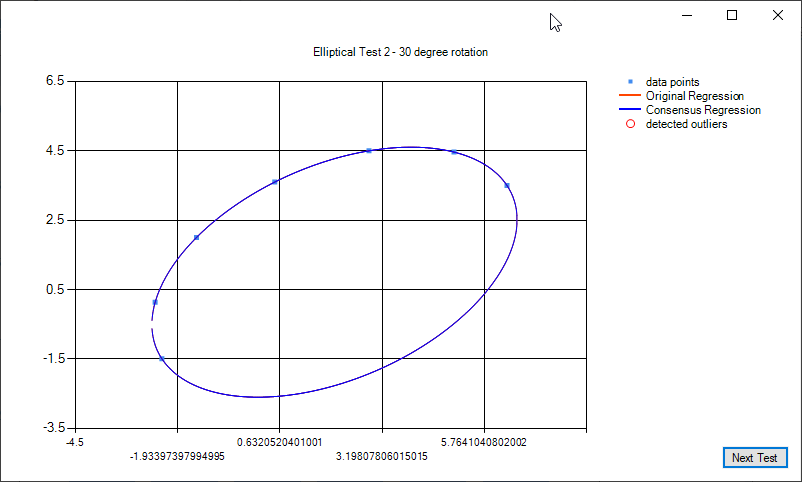
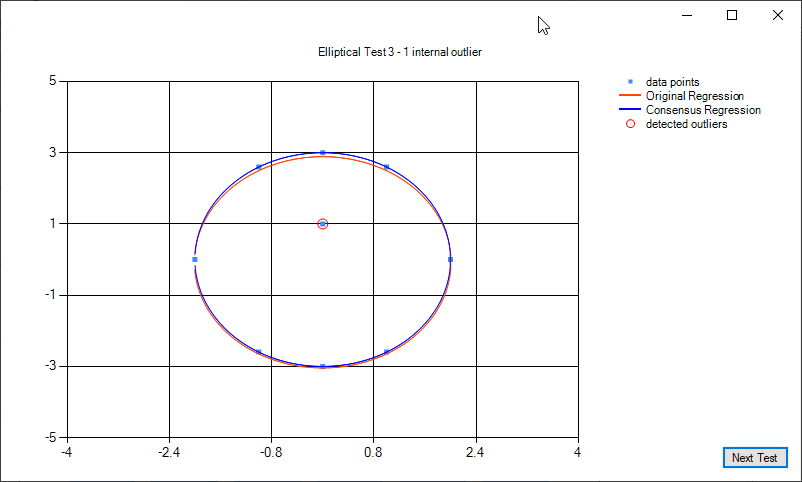
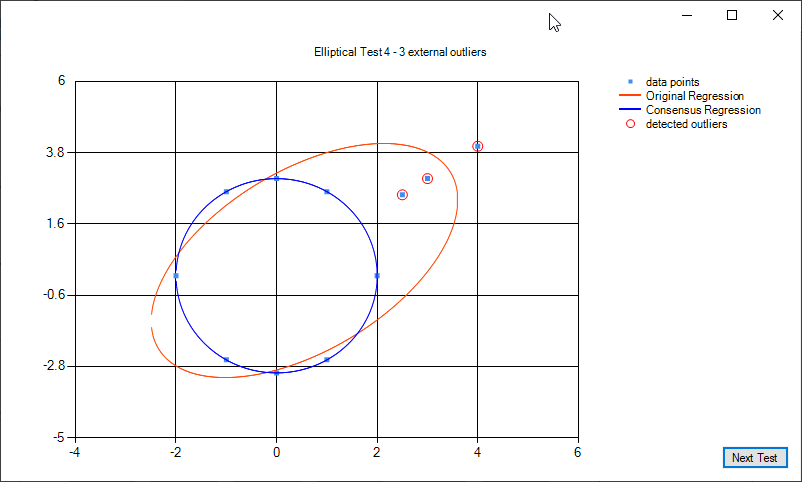
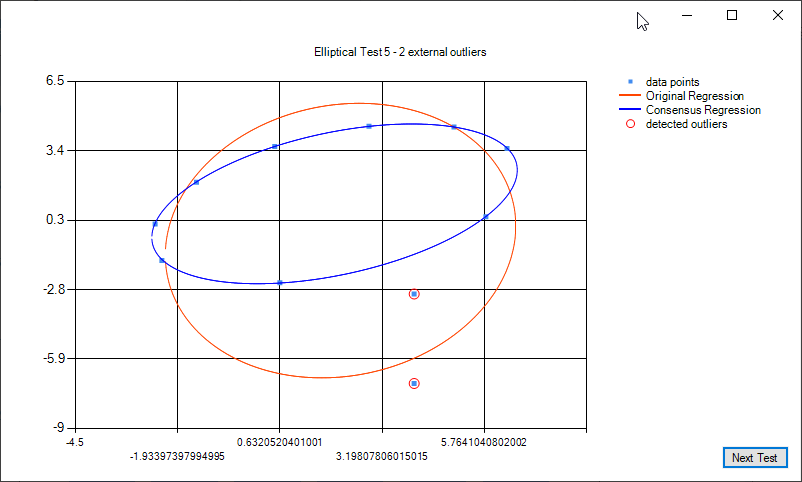
Some examples of elliptical regression and elliptical regression consensus:

On the algorithm. The algorithm takes some inspiration from RANSAC but where RANSAC builds random models from the smallest subsamples, this algorithm starts with all datapoints and iteratively labels and removes outliers. Instead of an exhaustive search the the worst outlier to remove, only 3 candidates are considered. Two of the candidates are those candidates with the greatest regression error "above" and "below" the model (substitute "left"/"right"/"inside"/"outside"). Since the summations was kept for the least squares calculations, removing an outlier is generally as simple as decrementing these summations. Originally, only two candidates were going to be considered but in testing this initial algorithm it was not removing outliers for some "easy" cases. I added a third candidate which is the candidate with maximum "influence"; this is generally the data point with maximum x * y. Finally, iteration is stopped when the model's average regression error goes below a threshold.

For display, C# Chart utility was used.

There is a parallel C++ implementation of these utilities at https://github.com/merrillmckee/regressionUtilsCpp