Implement operation simplification with circuit identities / templates

[glassnotes]

Please describe what you would like the feature to accomplish.
For resource estimation, it would be great to be able to simplify gate sequences in operations based on a standard (or user-defined) set of rules, essentially like a transpiler pass. As it stands, the ResourcesEstimator does not perform any simplification and so overestimates the number of gates that would actually be required (see example below). There are also instances where one may want to simplify based on a different elementary gate decomposition (e.g. a different arrangement of Clifford+T for the Toffoli, or taking advantage of shared control/target simplifications).

---

Describe the solution you'd like
Two things:

1. A basic library of circuit simplification identities and templates that can be applied "out of the box". For example, the ability to wrap an operation with another operation called Simplify, that checks for things like adjacent gates that cancel. Perhaps this could have different levels of optimization like classical compilers (e.g. level 1 just removes neighbouring operations that cancel out, while a higher level performs multiple passes and does things like pushing gates around based on commutation relations).
2. A framework for specifying and applying user-defined decompositions. Perhaps there is a type for a template that takes an operation and returns the desired implementation, that can be passed as an argument to said Simplify function.

Here is a pseudocode example of what I'm imagining (please excuse my syntax):

// User-specified template
CircuitIdentity SharedControlToffoli(Operation) {
    // Given an adjacent pair of gates, check if they are 
    // a Toffoli with shared control; if so, return a Clifford+T 
    // decomposition that takes advantage of simplifications.
}

// Some operation
operation MyOperation() {
    using (q = Qubit[5]) {
        CCNOT(q[0], q[1], q[2]);
        CCNOT(q[0], q[3], q[4]);
   }
}

// Perform the operation
Simplify(MyOperation());  // Some sort of default pass
Simplify(MyOperation(), optimizationLevel=2, userDefinedTemplates=[SharedControlToffoli]); // Add more optimization

---

Describe alternatives you've considered
So far, simplification by hand, or implementing a circuit in a different framework, using its transpiler, and then reimplementing in Q#. This is okay for a few, small circuits, but not sustainable for larger circuits.

---

Additional context
As an example, consider the following operation:

    operation ApplyMultipleH() : Bool {
        using (q = Qubit[1]) {
            H(q[0]);
            H(q[0]);
            let value = ResultAsBool(M(q[0]));
            ResetAll(q);
            return value; 
        }
    }

This yields resource counts as below:

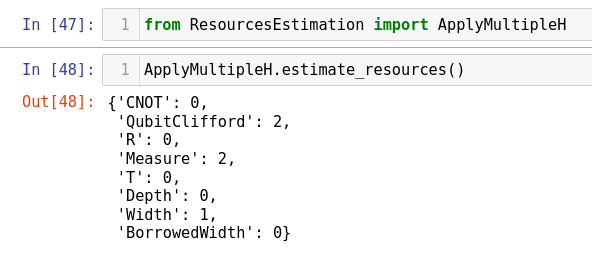
It should be able to determine that the adjacent H cancel out and remove them from the circuit.

[bamarsha]

Hi @glassnotes, I believe this was transferred to the compiler repository because it looks like your examples can be simplified at compile-time. This wouldn't work if the simplifications depend on runtime values and/or branching, but if not, we do have a compile-time circuit optimizer that @rsoiffer worked on last summer, although it's currently experimental and not enabled by default. I think that it could probably handle your examples of adjacent CNOTs and Hs after some configuring.