Finding optimal graph structures, an optimization problem that has applications in several areas including machine learning itself, such as Bayesian Network Learning.
Finding optimal graph structures is an important optimization problem that has applications in several
areas including machine learning itself, such as Bayesian Network Learning. The problem of Bayes- Net Learning can be simplified as the vertex ordering problem. Given a set of vertices the goal is to
determine a vertex ordering with the minimum cost. Consider the network below, which can be represented by the ordering (B, C, A):
Consider the following optimization problem. We are given vertices V1, · · · , Vn and possible parent sets for each vertex. Each parent set has an associated cost. Let O be an ordering (a permutation) of the vertices. We say that a parent set of a vertex Vi is consistent with an ordering O if all of the parents come before the vertex in the ordering. Thus, (C, B, A) would be an inconsistent ordering for the above network. Let mcc(Vi,O) be the minimum cost of the parent sets of vertex Vi that are consistent with ordering O. The task is to find an ordering of vertices O that minimizes the total cost of the network: mcc(V1, O) + · · · + mcc(Vn, O): As an example, consider that you are not given the network above. Instead you are given the vertices A,B, and C and their possible parent sets along with their cost as follows and given the task of finding the minimium cost network.
The cost of ordering (B,C,A) is cost(C→{B}) + cost(A→{B,C})) = 2.4 + 6.3 + 1.3 = 10 whereas the cost of ordering (A,B,C) is cost(C→{B}) + cost(B→{})) = 7.5 + 6.3 + 2.4 = 16.2 Your task is to implement and experiment with the search algorithms(BFS, DFS, UCS) discussed in class for finding a good ordering of the variables. Three datasets are made available for you to experiment on (in addition to the two simple examples described in this document). You will implement the search algorithms in Python and will submit a Python notebook that prints the minimum cost ordering as well as its cost. Consider the following short data file.
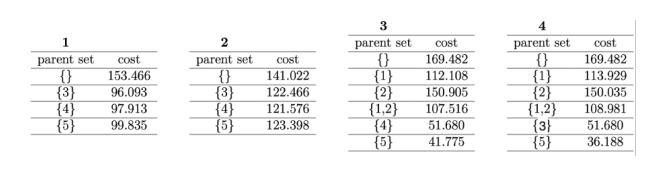
which represents the following example:
Consider the ordering (5, 3, 1, 4, 2). With respect to vertex 1, the parent set {4} is not consistent with the ordering. The parent sets {}, {3}, and {5} are consistent with the ordering The ordering (5, 3, 1, 4, 2) has a total cost of 96.093 + 121.576 + 41.775 + 36.188 + 169.802 = 465.435. whereas the ordering (1, 2, 3, 4, 5) has a total cost of 153.466 + 141.022 + 107.516 + 51.680
- 36.508 = 490.192