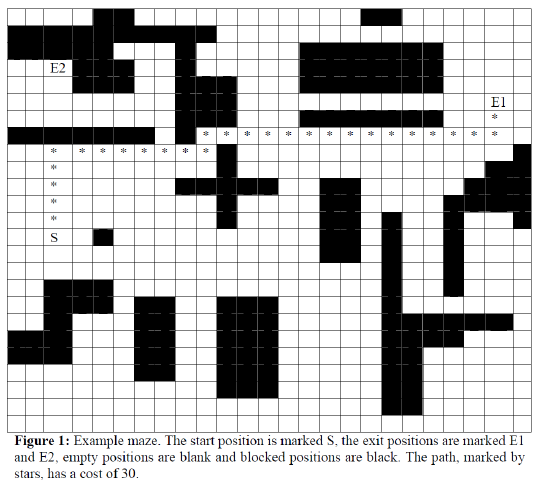
Assume a 25 × 25 two-dimensional maze. Each square in the maze has an (x,y) coordinate, with the bottom-left corner being (0,0) and the top-right corner being (24,24). Each position in the maze can be either empty or blocked. In addition, there are two “special” positions, the starting position and the exit position. The agent can only move up, down, left or right, but never diagonally. It also cannot enter blocked positions or move outside the maze. Its objective is to find a path from its starting position (S) to the exit position (E1 or E2), preferably the cheapest one. The cost of a path is the number of positions the agent has to move through, including the starting and exit position. The map of the maze is given in the figure below.
Implement a code to find a path from the starting position to an exit position using random search. In random search the next move is selected randomly from any of the possible moves in the current state. Assume the agent can not immediately go back to the state that it came from (It can go back to that state later in the search). Limit the total number of moves to 1k (1000), 10k, 100k, and 1000k. For each experiment, report on whether the agent is able to find an exit or not. If it found an exit, which exit was found and what is the path cost from S to that exit. If no exit was found, report your thoughts on the reason to that.