-
Affine Transformation을 활용한 함수다.
-
Affine Transformation은 선형변환(Y = WX)에서 +b를 추가하여 벡터에 위치 이동의 개념을 추가시킨 것이다.
-
아핀 공간은 벡터에 위치의 개념을 추가시킨 것이다.
Linear Transformation -> Y = WX Affine Tarnsformation -> Y = WX + B
Affine Function은 데이터와 실제값 사이의 규칙을 찾는 과정을 거쳐 만들어진 식이다. 즉, 주어진 훈련데이터로 입력데이터인 X와 실제 값인 Y간의 규칙을 찾아 적당한 W와 B값을 할당 시켜 만들어진 식이라는 것이다.
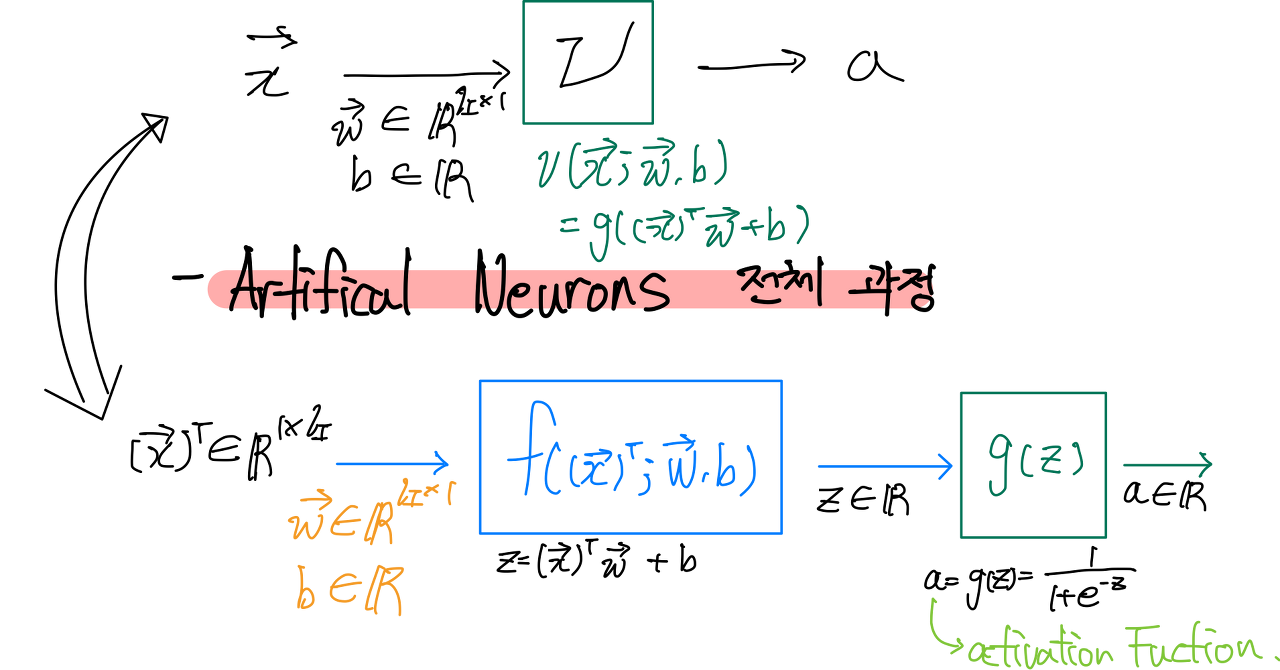
Artificial Neuron이란, 신경해부학적 사실을 토대로 하여 만든 인공신경망 기본구성요소로, 단순한 연산기능을 가지고 있는 수많은 인공뉴런이 서로 연결되어 정보를 저장하고 처리한다는 개념이다.
위 그림은 Artificial Neurons의 전체 과정으로 affine function과 activation function의 파트로 나눠지고 affine function에서 계산된 값을 activation function에서 한번더 연산을 하는 과정이다.
Activation Function은 affine function에서 만들어진 식을 통해 나온 Y값을 sigmoid/tanh/relu 등의 식에 대입하여, 보다 정렬된 값으로 변형시켜주는 식이다.
그러면 왜 우리는 Activation Function을 사용해야하는가?
-선형시스템이 아닌 비선형 시스템으로 변형시키기 위해서다. 이렇게 말하면 잘 와닿지 않을 것이다.
선형시스템은 한계가 있다. XOR문제는 다들 알 것이다.
선형시스템은 AND와 OR문제는 해결할 수 있지만, XOR과 같은 non-linear한 문제는 해결할 수 없다는 한계가 있다.
그리고, 선형시스템은 아무리 layer들을 쌓아 깊게 구현한다고 해도 f(ax+by)=af(x)+bf(y)의 성질 때문에 결국 하나의 linear연산으로 나타낼수 있다.
이에 대한 해결책이 Activation Function을 통해 출력값을 비선형 시스템으로 만드는것이다.
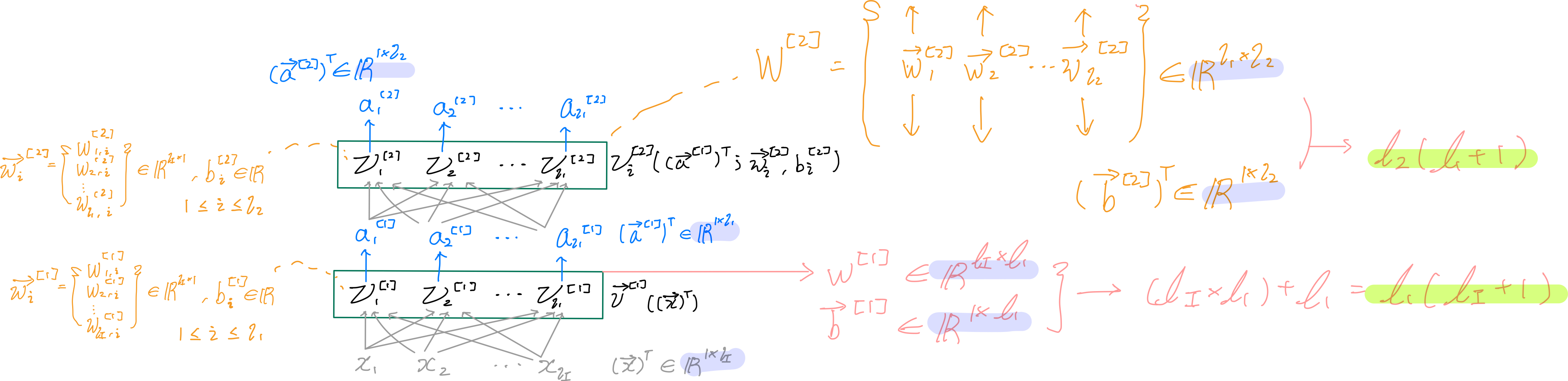
Layer는 서로 다른 Parameter(Weight, Bias)들을 가지고 있는 Parametric Function들의 모임이다.
즉, Neuron들의 집합이라고 생각면된다. 다양한 Neuron들이 하나의 층을 형성하고 그것을 layer라고 부른다.
그리고, Dense Layers는 모든 입력값(x1,x2,x3,x4,xli)가 각각의 뉴런에 모두 들어가는 것을 말한다.
- Input vector (vector X transposed)가 ℓI(엘아이)개 있기 때문에 Weight(vector W)도 ℓI개 있어야한다.
그 이유는 행렬곱의 개념을 가져와 실행하기 때문인데, 행렬곱은 XY인 경우에 X의 열의 개수와 Y의 행의 개수가 같아야 각 원소끼리 곱하면서 더해져가기 때문이다.
- Neuron이 ℓ1개 있으면 weight 자체, bias 자체도 ℓ1개 있다.
그 이유는 각 neuron에 각 weight와 bias가 할당되어 있을 거기 때문이다. 이부분이 하나의 layer에서는 당연한 말이라고 생각되겠지만, 층이 깊어질 수록 헷갈려질 수 있다. 유의해놓자.
- Input 값 X의 열 개수와는 관계없이 결괏값 a vector는 neuron의 개수 ℓ1과 연관된 vector (1,ℓ1) 형태다.
이유는 X ∈ R(1xℓI) 가 들어오면, 우선 W(metrix) ∈ R(ℓIxℓ1)와 행렬곱을 실행하여, bias(vector transposed) ∈ R(1xℓ1)와 더해주면, (1 x ℓI) * (ℓI x ℓ1) + (1 x ℓ1) = (1 x ℓ1)로 결괏값 a vector는 shape = (1 , ℓ1)가 된다.
- 결괏값 a는 X * W + b 의 결괏값 Z에 activation function인 g( ) 을 진행해줘서 나온 값이다.
-
각 layer별 파라미터 개수는 ℓI (Input data X의 행 개수) x ℓ1(현재 layer의 neuron 개수) + 1 x ℓ1(현재 layer의 neuron 개수)다.
-
이전 layer의 결괏값 a1이 다음 layer의 입력값으로 들어가고 이에 맞게 weight와 bias 개수가 할당 되어 연산된다.
sigmoid를 알기 전에 Logit을 알아야하고, Logit을 알기 전에 odds 를 알아야한다. 그 이유는 sigmoid는 odds에서 변형되어, 탄생됐기 때문이다.
odds ratio는, 한 사건이 일어날 확률 대비 한 사건이 일어나지 않을 확률의 비율?이라고 생각하면 된다. 예를 들어, 동전을 던질 때, 뒷면이 나올 확률 대비 앞면이 나올 확률은 1이다. 두 확률이 동일하기 때문이다.
odds 식은 O = P/1-P 다.
odds ratio는 아래와 같은 그래프를 형성한다. (확률이 1에 가까워 질수록 양의 무한이 되는 것을 볼 수 있다.)
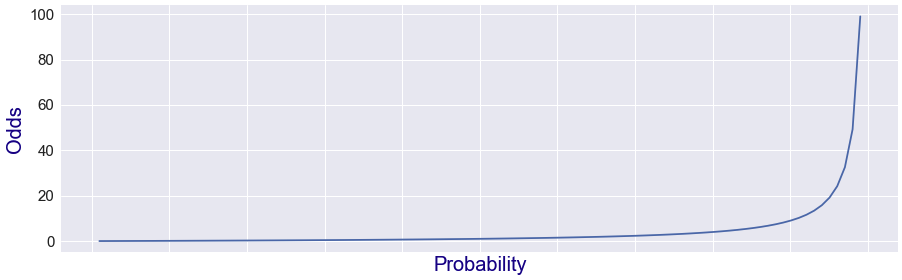
Logit 함수는 odds에 log를 씌운 것이다. odds의 다른 표현이라고 생각하면 된다. odds에 log를 씌운 이유는 연산하기 수월해지기 때문이다.
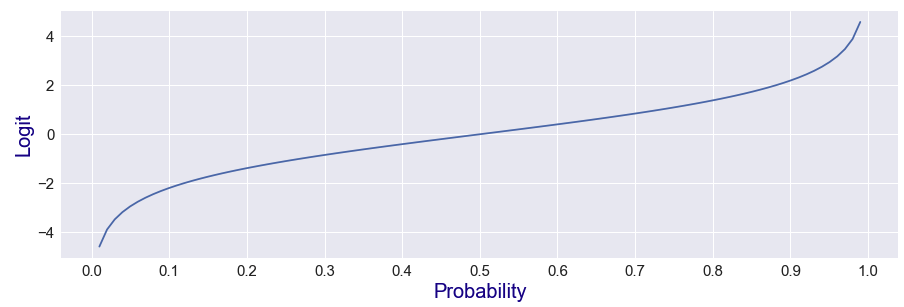
logit 함수의 식은 Logit = log(p/1-p) 다. logit 함수의 특징은 확률 0.5를 기준으로 logit 값이 음수와 양수로 나뉜다. logit 함수의 그래프는 아래와 같다.(확률이 0에 가까워 질수록, 음의 무한이 / 1에 가까워 질수록, 양의 무한이 된다.)
sigmoid 함수는 logit 함수를 "p =" 형태로 변형시킨 것이다. 즉, 값이 확률을 의미하도록 변형시킨 식이라고 생각하면 된다.
logit 값을 확률로 변형시킨 이유는 Binary Classifiers에서 마지막 결과가 확률의 의미를 가지는 값이 나와야하기 때문이다. (&두 분류로 나눠야하기 때문.)
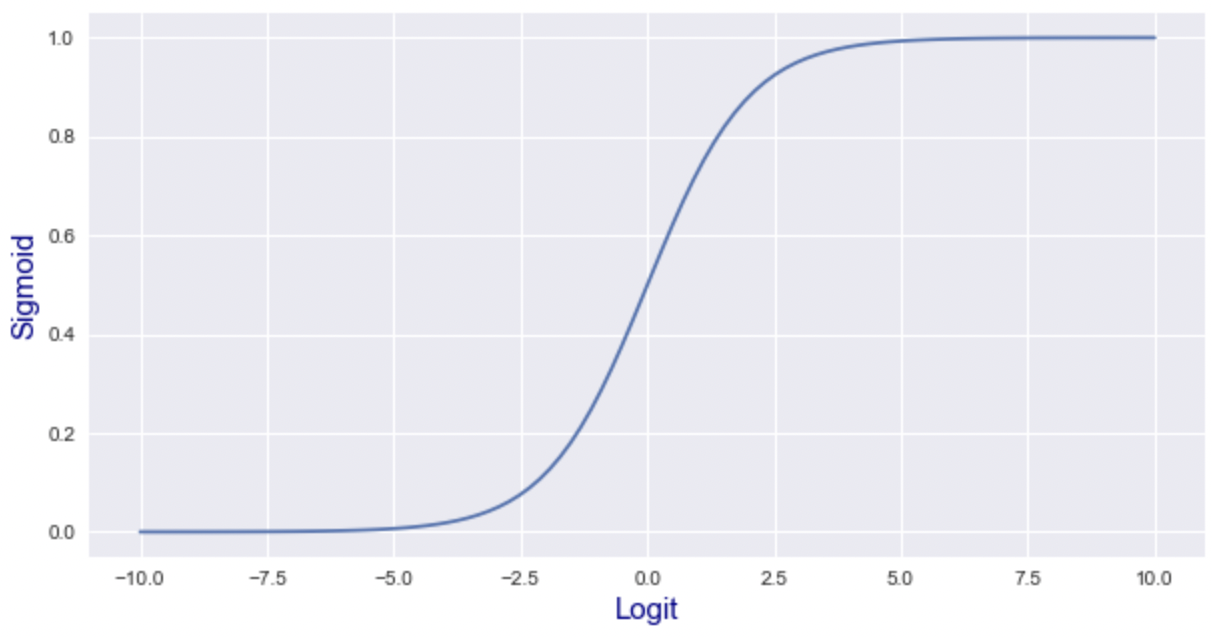
sigmoid 그래프 결과는 아래와 같다.(Logit값이 음의 무한으로 가면, sigmoid값은 0에 수렴하고, Logit값이 양의 무한으로 가면, sigmoid값은 1에 수렴한다.)
※딥러닝에서는 Affine Function을 거쳐 나온 Z값을 Logit 값으로 생각하여 activation Function중 sigmoid에 넣어 나온 P인 확률값을 최대한 실제 확률값으로 만드는 것이 목표다.
마지막 layer에 Sigmoid activation Function을 실행할 Neuron을 하나 추가하여 마지막 Output이 확률값이 되도록 한다.
Binary Classification을 위한 Output을 만들어준 것이다. Binary Classification이란 2개의 범주형 데이터를 활용한 분류를 말한다.
또한, 위 과정의 러닝을 Logistic Regression이라 한다.
독립 변수의 선형결합(affine Function)으로 종속변수를 설명하는 선형회귀와 비슷하지만, 종속변수가 범주형 데이터를 대상으로 하여 일종의 분류 기법으로도 볼 수 있다.
회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도학습 알고리즘이다.
머신러닝에서 Binary Classification 모델로 사용되는 것이 로지스틱 회귀 알고리즘이다.
softmax layer는 다양한 class를 분류하여 확률을 계산할 때, 사용한다.
위 그림과 같이 한번에 다양한 데이터를 입력하여, 각 데이터에 대한 확률값을 도출해내야할 때, 사용된다.
각 데이터에 관하여, 도출된 확률값들의 합은 무조건 1이 되어야한다.(당연한 말이기도 하다.)
Softmax 이전 layer에는 activation Function을 사용하지 않거나, linear Function을 사용한다. 그 이유는 softmax 역할을 하는 layer가 이 후에 나와서, activation Function과 같은 역할을 해야하기 때문이다.
다양한 분류가 필요할 때, 사용된다.
Softmax 이전 layer의 neuron 개수는 logit 값의 개수와 동일하고, softmax layer의 출력값인 provability의 개수와 동일하다. 입력 데이터의 크기가 (N X ℓ0-1)으로 들어온다면, softmax 이전 layer에서는 neuron개수(ℓ0)로 인해 (N X ℓ0)가 될 것이고, softmax layer에서는 이에 맞는 softmax 개수가 나오므로, (N X ℓ0)크기의 provability 개수가 나올 것이다.
Softmax Layers와 Sigmoid의 Neuron Network 구성에서의 차이점은 아래와 같다.
-
Softmax 는 하나의 layer가 softmax의 역할을 하고 Sigmoid는 하나의 layer에서 Affine Function을 거친 Activation Function중 하나의 함수다.
-
Softmax는 이전 layer에서 logit값을 받고 Sigmoid는 현재 layer 속에서 Affine Function을 거친 값을 logit으로 한다.
-
Softmax는 logit vector를 받아서 provability vector를 추출하고, Sigmoid는 logit 1개를 받아서 provability 1개를 추출한다.