In the computer science, very important and intial.
we have to obtain familiar with C++.
I'm using Java and C++.
First, Second, step by step...
🔥 FIRE!!
LIFO(Last in First Out): defined basic linear list
Stack application two calculate:
1) Push: stack에 원소 저장
2) Pop: stack으로부터 원소 가져옴
Stack으로부터 원소를 pop하면 그 원소가 가장 마지막에 넣은 원소임을 보장
구현 형식: Top위치가 중요!👍👍 맨 마지막에 넣은 위치를 저장(-1로 초기화)
push(top ++) 함수: top의 위치를 return 함
pop(top --) 함수: top의 위치를 return 함, 그리고 empty를 통해 비었는지 확인
full 함수: 원소가 주어진 크기보다 크다면 원소를 추가 할 수 없도록 한다.
empty 함수: top의 위치가 0보다 작아지는 경우라면 판단 (top을 어떻게 초기화를 했는지에 따라 다름)
FIFO(First in First Out)
Queue application two calculate:
1) Insert: queue 한 개 원소를 저장
2) delete: 한 개 원소를 취함
구현 형식: rear위치에서 insert, front에서 delete가 이루어짐 / data: front, rear, array 선언
Insert : rear위치에 원소를 넣고 rear ++ 한다.
Delete : front의 위치의 원소를 가져오고 front ++ 한다.
empty 함수: array 에 원소가 없는지 확인
full 함수: array에 원소 모두 차서 공간이 부족한 경우
Circular Queue: Array 사용하여 Queue 구현 시 문제가 생깁니다.
1) rear, front 모두 증가하면 array 끝에 rear가 도달하면 더 이사 원소 추가가 불가능!
앞 쪽의 delete 이루어지 공간은 사용이 🔥 가능. So, ⭕️ Queue 사용
2) full, empty 구분을 못하게 된다. array 전체 공간이 모두 full되면 front, rear가 같은 위치가 되어 초기 empty상태와 동일하게 된다.
⁉️ 해결: 마지막 남은 한 개의 빈 공간은 사용하지 않도록 한다. front 직전 마지막 원소가 비어있는 상태인 full로 판단하게 함
rear, front 증가는 아래와 같이 나머지 연산을 사용
유한 개의 노드로 이루어지며, Root node 특별히 하나만 가진다.
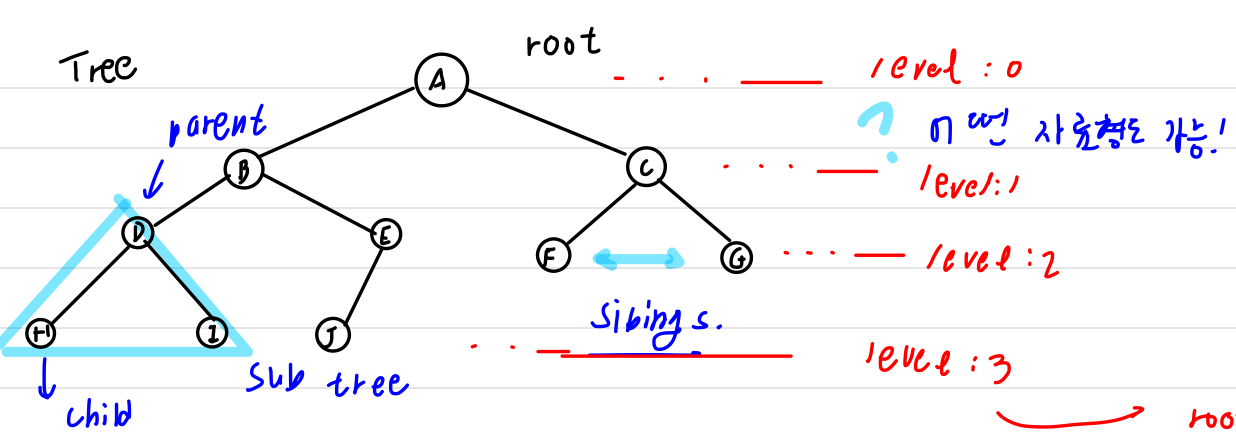
Node(트리구성 기본구조) Parent Node(부모노드) Siblings node(형제노드; 같은 부모) branch(node와 node간 연결) Edge(가장 긴 노드간 연결) Heigh(가장 긴 루트 경로 길이) degree of a node(각 노드의 자식노드 개수) degree of tree(트리 최대 차수) Leaf(terminal node)-(자식이 없는 노드: degree 0) Internal node(degree > 0) ancestors(자신과 root상 path 존재 노드)
Binary Tree(이진트리): 모든 노드 차수가 최대 2인 형태


