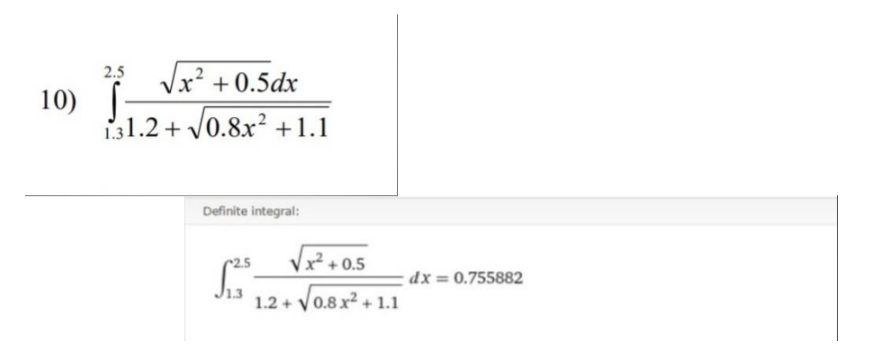PRiR-Homework - multi-thread programming

PD_11_10 - the first program for NUMERICAL INTEGRATION (methods Simpson, rectangle method, trapezoidal method)
PD_22_10 - the second program about Zoo ( real world simulation system )

PD_11_10

I made three classes for each method to represent the area of one figure as a thread.
First one: M_prostokatow - consists in dividing the integration interval into rectangles and calculating the area of these rectangles.
The accuracy of calculations in all methods depends on the number of these divisions, i.e. rectangles.\

Sample integral in this program:

Variable initialization

  	private float a; // beginning of the integration interval
	private float dx; // the length of one interval, i.e. the rectangle after the division 
	
	private double w_calka; // integral value
	private int i; // the iteration number, i.e. the thread or rectangle

Constructor

Method start() = run()
If you add join() here, threads in the result will not go in random order.

public M_prostokatow(double w_calka, int i, float a, float dx){
	this.a = a;
	this.dx = dx;
	this.w_calka = w_calka;
	this.i = i;
	start();
}

Method run()

Count the areas of successive rectangles.
mojPrzyklad.funkcja1() - a static function with an example integral.
Writing to the console the value of the next thread = rectangle.
In a static variable -> wynik_prostokaty from the main class we sum the result.

public void run() {
	w_calka = mojPrzyklad.exampleTen(a+i*dx);
	System.out.println("M_Prostakat nr-" + i + " ma wartosc calki = " + w_calka);
	main_task_1.wynik_prostokaty += w_calka;
}

This method in class main_task_1

// parametrs
    	float xp = (float) 1.3;
	float xk = (float) 2.5;
	int n = 4;
	float dx = (xk - xp)/n;
// main loop - creating threads
    	for(int i = 1; i <= n; i++) {
		new M_prostokatow(wynik_prostokaty, i, xp, dx);
	}
// write the result to the console
    	wynik_prostokaty *= dx;
	System.out.println("---------------Wyniki---------------");
	System.out.println("Metoda prostokatow: Pole --> " + wynik_prostokaty);

The class for trapezoidal method

By analogy with rectangle method, but with a some difference.

1. Another formula for calculating the trapezoidal area = thread

public void run() {
	if(i == 0 || i == n) {
		w_calka = mojPrzyklad.exampleTen(a+i*dx)/2;
	} else {
		w_calka = mojPrzyklad.exampleTen(a+i*dx);
	}
	...

2. Main loop starts with 0

for(int i = 0; i <= n; i++) {
	new M_trapezow(wynik_trapezy, i, xp, dx, n);
}

wynik_trapezy *= dx;
System.out.println("Metoda trapezow: Pole --> " + wynik_trapezy);

Class for Simpson method

By analogy with previous methods, but with some difference.\

1. Difference in the field calculation - depending on the parity of the iteration number

public void run() {
	if(i == 0 || i == n) {
		w_calka = mojPrzyklad.exampleTen(a+i*dx);
	} else if(i%2 == 0) {
		w_calka = 2*mojPrzyklad.exampleTen(a+i*dx);
	} else {
		w_calka = 4*mojPrzyklad.exampleTen(a+i*dx);
	}
	...

main_task_1

	wynik_simpsona *= (dx_simpson/3);
	System.out.println("Metoda Simpsona: Pole --> " + wynik_simpsona);

RESULTS

1. Without join()
   
2. With join()
   
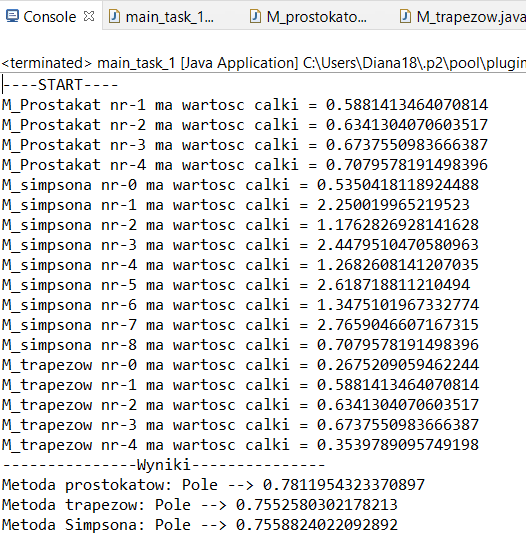
   The best method of calculating the integral - method Simpsona.
   Method analysis :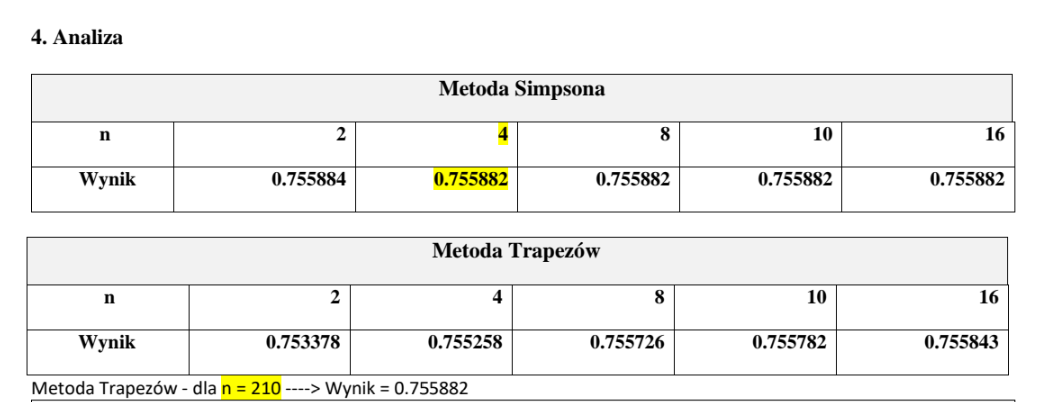

PD_11_10

Zoo with aviaries with various animals.
They may or may not be hungry.
People work in these aviaries, that is, they watch the animals.
If there is not enough food, the worker can order supplies.
If the animals are very hungry and there are not enough supplies ordered, it could be a disaster, so the zoo is closed.

Results