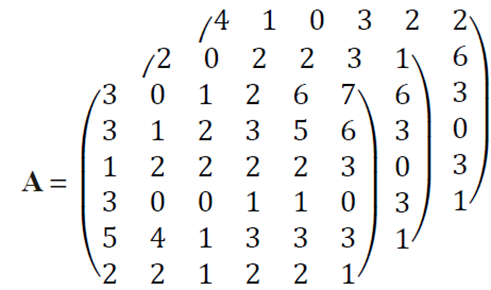layout	use_math	date	title	tag
post	true	2022-12-16	Machine Learning 오일석	Machine Learning

2년 전 위 책으로 공부했던 내용을 정리 해보고자 한다.
이 책은 처음 기계 학습에 대해 공부하고자 하는 분들에게 좋은 책이다. 책의 설명이 쉽기도 하고 유튜브에 "오일석 기계학습"을 검색하면 강의를 볼 수 있어 편하게 공부했었다.

Machine Learning

목차

0. Machine Learning
   • 목차
1. Chapter 1 : Intoduction
   • Chapter 1.1 : 기계 학습과 특징
     • 간단한 기계학습 예제
     • 다차원 특징 공간
   • Chapter 1.2 : 데이터에 대한 이해
     • 목적 함수(Objective function)또는 비용 함수(Cost function)
   • Chapter 1.3 : 모델 선택
     • 과소적합(underfittinig)과 과대적합(overfitting)
     • 편향(Bias)과 분산(Variance)
     • 모델 선택 알고리즘
     • 규제(Regularization)
   • Chapter 1.4 : 기계학습의 여러 학습 방법
     • 지도 학습(Supervised Learning)
       • 분류 방법
     • 비지도 학습(Unsupervised Learning)
     • 강화 학습(Reinforcement Learning)
2. Chaepter 2 : Machine Learning and Math
   • Chapter 2.1 : 선형대수
     • 벡터(Vector)
     • 행렬(Matrix)
     • 텐서(Tensor)
     • 놈(Norm)과 유사도
     • 퍼셉트론(Perceptron)
     • 행렬 분해
     • 역행렬

Chapter 1 : Intoduction

우리는 태어나서 여러가지를 보고 듣고 느끼며 꾸준히 학습하고 있다.
그렇다면 기계는 어떻게 학습하는지를 공부하고 답을 찾아가기 위한 책이다.

Chapter 1.1 : 기계 학습과 특징

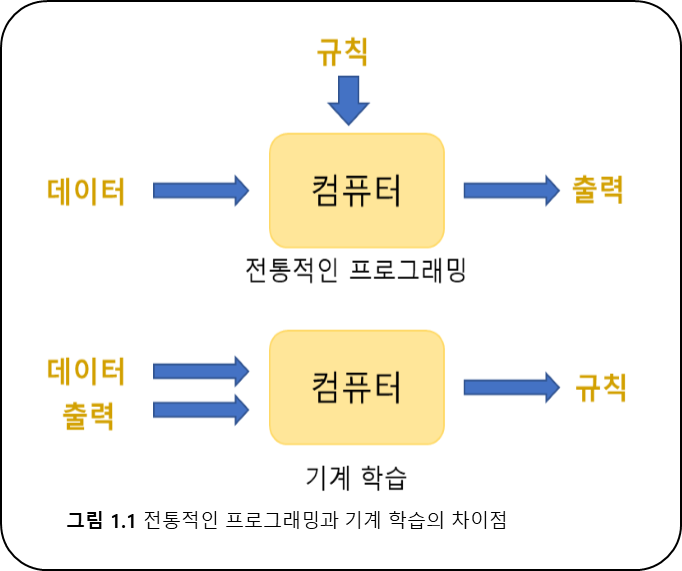
• "컴퓨터를 통한 학습" 기계 학습이다.
• 경험, 데이터를 기반으로 학습하고 예측하는 것이다.

• "프로그램을 명시적을로 작성하지 않고 컴퓨터에 학습할 수 있는 능력을
  부여하기 위한 연구 분야이다."

간단한 기계학습 예제

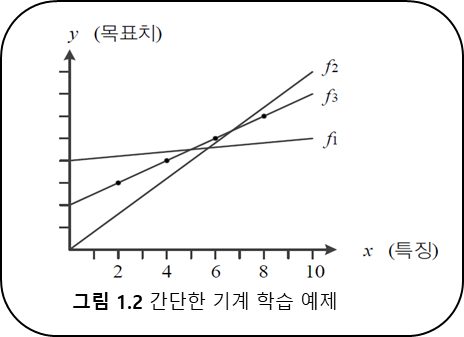
• 가로축은 시간, 세로축은 위치이다.
• 임의의 시간이 주어지면 이동체의 위치를 예측하라.

• 훈련집합과 직선 모델
• 따라서 $x\in\mathbf{X}$와 $y\in\mathbf{Y}$를 설정한 모델에 넣어 가며
  최적의 매개변수 $w$와 $b$를 찾아가는 것이다.

$$\mathbf{X}=\begin{Bmatrix}x_1,x_2,\dots,x_n\end{Bmatrix}, \mathbf{Y}=\begin{Bmatrix}y_1,y_2,\dots,y_n\end{Bmatrix}$$

$$y=wx+b$$

• 처음에는 임의로 설정한 매개변수에서 학습을 마치면 훈련집합에 없는 데이터에 대해서 예측을 가능하게 된다.

다차원 특징 공간

• 위는 $x$의 값에 따라 $y$를 예측하기 위해 매개변수$w,b$를 찾아보았다.
• 이제 여러개의 특징들을 가진 데이터의 결과를 예측해 본다.

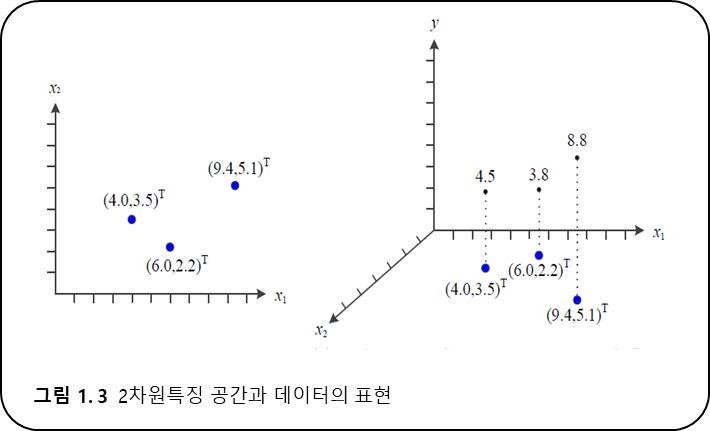
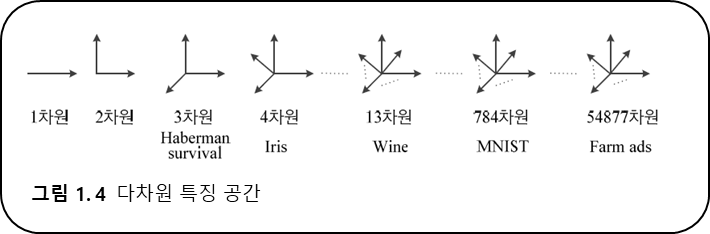
• 다차원 데이터는 다음과 같이 표현된다. $$\text{특징 벡터 표기 : }\mathbf{x}=(x_1,x_2,,\dots,x_d)^T\in\mathbf{X}$$

$$\text{훈련 집합 : }\mathbf{X} = \begin{Bmatrix}\mathbf{x}_1,\mathbf{x}_2,\dots,\mathbf{x}_n\end{Bmatrix}$$

$$\mathbf{Y}=\begin{Bmatrix}y_1,y_2,\dots,y_n\end{Bmatrix}$$

• 학습 모델
  • 모델이 1차 직선인 경우 매개변수의 수는 $d+1$이다.
  • 모델이 2차 곡선 모델인 경우 매개변수의 수는 $d^2+d+1$이다.

$$\text{다차원의 직선모델 : } y=w_1x_1+w_2x_2+\dots+w_dx_d+b$$

위로 가기

Chapter 1.2 : 데이터에 대한 이해

• 데이터 생성

  • 주사위 같이 데이터의 발생 확률을 알고 있다면 새로운 데이터를 생성 할 수 있다.
  • 보통 기계 학습 문제에서는 데이터 생성 과정을 알 수 없다.
  • 주어진 훈련 집합을 통해서 근사 추정할 수 있을 뿐이다.

• 데이터베이스의 품질

  • 주어진 응용 환경에 맞는 데이터베이스릐 확보는 중요하다.
  • 자주 쓰는 데이터는 Iris, MNIST, ImageNet과 같은 데이터 세트이다.
    

목적 함수(Objective function)또는 비용 함수(Cost function)

• 목적 함수는 기계학습에서의 목적을 가진 함수이고, 즉 목표치와 예측치사이의 오차를 줄이는 함수를 의미한다.
• 예측함수의 출력 : $f_\boldsymbol{\theta}(\mathbf{x}_n)$
  • $\boldsymbol{\theta}$는 매개변수 집합이다.
• $y_n$는 목표값이고, $f_\boldsymbol{\theta}(\mathbf{x}_n)-y_n$는 예측과 목표의 손실 오차(Loss function)다.
• 아래 식은 평균 제곱 오차(MSE; Mean Squared Error)이다.

$$J(\boldsymbol{\theta})=\frac{1}{n}\sum_{i=1}^n(f_\boldsymbol{\theta}(\mathbf{x}_i)-y_i)^2$$

위로 가기

Chapter 1.3 : 모델 선택

• 내가 가지고 있는 상황에 따라 어떤 알고리즘을 선택하고, 어떤 데이터 처리방식을 선택하는지 정해진 답은 없다.
• 경험적인 접근방법이나 여러가지 규제(regularization)을 적용한다.

• "To some extent, we are always trying to fit square peg(the data generating process) into a hole(our model family)." 어느 정도 우리가 하는 일은 항상 둥근 홈(우리가 선택한 모델)에 네모 막대기(데이터 생성 과정)을 끼워 넣는 것이라고 말할 수 있다.[Goodfellow2016]

과소적합(underfittinig)과 과대적합(overfitting)

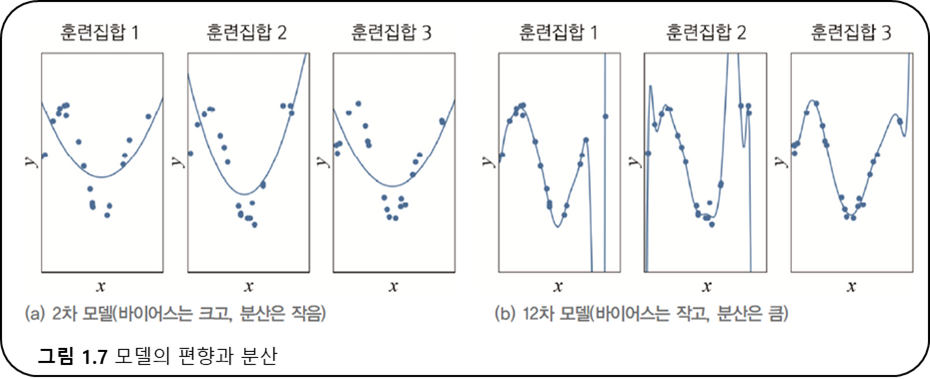
• 과소적합(underfitting)은 모델의 최적화가 진행되지 않은 상태이다.
• 과대적합(overfitting)은 훈련집합에 대해 거의 완벽하게 근사화, 그러나 새로운 데이터를 예측할 때 문제가 발생한다.

편향(Bias)과 분산(Variance)

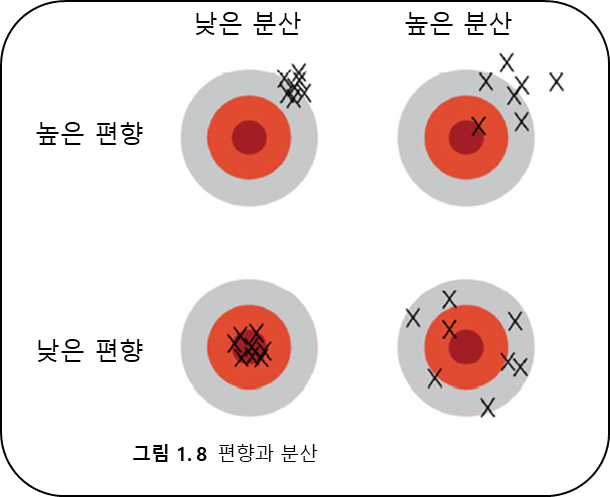
• 편향은 추정 값이 한 쪽 방향으로 치우침에 따라 나타나는 오차.

• 분산은 같은 모델들의 오차.

• 2차 모델은 편향이 크고 비슷한 모델을 얻으므로 분산이 낮다.

• 12차 모델은 편향이 작고 서로 차이가 큰 모델을 얻으므로 분산이 높다.

• 따라서 편향의 희생을 최소로 유지하며 분산을 최대로 낯추어야 한다.

모델 선택 알고리즘

• 여러 모델을 비교하여 성능을 측정하기 위한 검증집합을 이용한다.
• 교차검증은 훈련집합을 k등분하여 하나의 집합을 뺀 나머지를 학습하고 남은 하나로 측정하고, 이를 돌아가며 k법 측정하여 모델의 성능을 측정한다.
• 난수를 이용한 샘플링으로 모델의 성능을 측정하는 부스트트랩을 이용한다.
• 현실에서는 이러한 모델이 무수히 많기 때문에 경험을 통해서 큰 틀을 선택한 후, 세부 모델을 선택한다.

규제(Regularization)

• 데이터 확대
  • 실제 데이터를 얻기 위해서는 비용이 많이 든다.
  • 따라서 데이터를 변형함으로 인위적으로 데이터를 확대한다.
• 가중치 감쇠
  • 학습이 반복되면서 가중치가 커지는 것을 개선된 목적함수를 이용하여 가중치를 조절하는 규제 기법이다.

위로 가기

Chapter 1.4 : 기계학습의 여러 학습 방법

지도 학습(Supervised Learning)

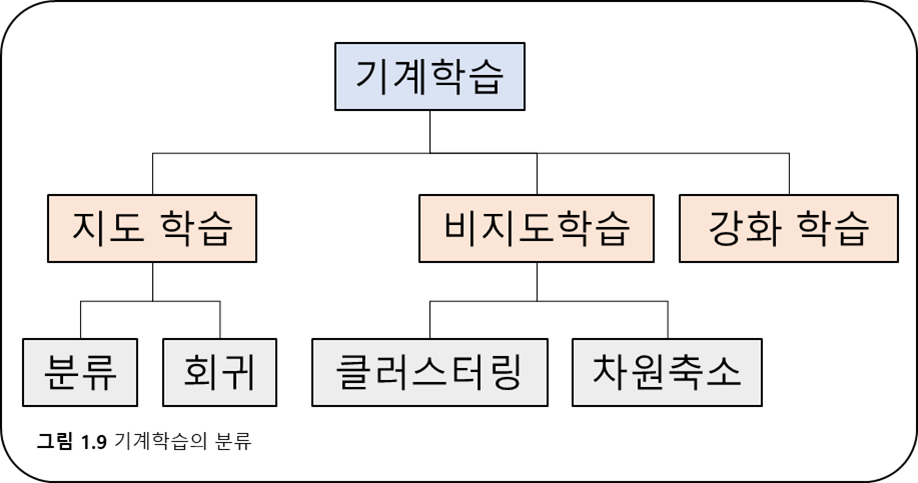
• 입력과 미리 알려진 출력을 연관시키는 관계를 학

1. 분류(Classification)

   • 유사한 특성을 가진 데이터끼리 묶어서 나누는 것
   • 2개로 분류하는 이항 분류, 그 이상의 다항 분류

2. 회귀(Regression)

   • 변수들 사이의 관계를 결정하는 통계적 측정
   • 회귀 분석 : 변수 사이의 회귀에 대해 검정이나 추정하는 것

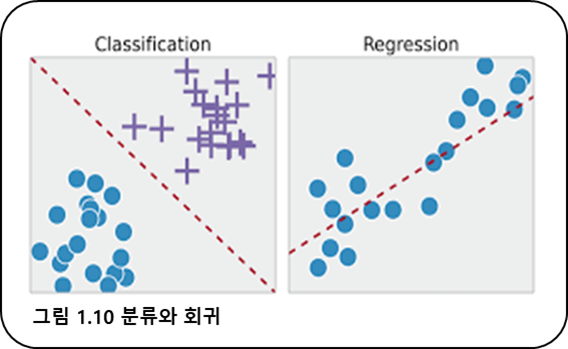
3. 분류와 회귀의 차이점

   • 분류는 일정한 기준에 따라 명백하게 구분 짓는 것
   • 회귀는 오차 제곱의 합을 최소화 하는 선을 긋는 작업

분류 방법

1. Naive Bayes 분류기
   • 자료의 분류를 베이즈 정리를 활용하여 판단.
   • 모든 특성값은 서로 독립
2. 의사결정 트리(Decision Tree)
   • 관측값과 목표값을 연결하는 예측 모델
   • 주택이나 자동차 구입비용 등의 추정에 활용
3. SVM(Support Vector Machine)
   • 데이터를 2개의 영역으로 분류하는 이진 분류기
   • 새로운 데이터가 어느 영역에 속하는지를 판단하기 위해서 가장 큰 여백을 가진 경계선을 찾는 알고리즘
4. K-Nearest Neighbor(K-NN)
   • '최근접 이웃 분류'라고도 불림.
   • 새로운 데이터와 가장 가까운 k개의 이웃 데이터들의 비율로 클래스를 결정

비지도 학습(Unsupervised Learning)

• 출력 값을 알려주지 않고 스스로 모델을 구축하여 학습
• 입력 값에서 규칙성을 스스로 찾아내는 것이 학습의 주요 목표

1. K-means 클러스터링
   • 대표적인 클러스터링 방법
   • 유사한 특성을 가진 k개의 데이터 그룹으로 묶는 방법
   • 각 클러스터에는 클러스터 중심이 있음

2. 추천 시스템(Recommender System)
   • 사용자의 정보를 모으고 정보에 기반하여 사용자에게 다른 정보를 추천하는 시스템

강화 학습(Reinforcement Learning)

• 목표값이 주어지는데, 지도 학습과 다른 형태이다.
• 바둑을 예로 들어 바둑의 수를 두는 행위가 샘플인데, 게임이 끝나면 목표값 하나가 부여된다.
• 게임을 구성한 샘플들 각각에 목표값을 나누어 주어야 한다.
• 자세한 내용은 9장에 나온다.

위로 가기

Chaepter 2 : Machine Learning and Math

• 수학은 목적함수를 정의하고, 목적함수가 최저가 되는 점을 찾아주는 최적화 이론을 제공한다.
• 최적화 이론에 규제, 모멘텀 기법, 학습률 제어, 멈춤 조건과 같은 제어를 추가하여 알고리즘을 구축한다.
• 사람은 알고리즘을 설계하고 데이터를 수집한다.

Chapter 2.1 : 선형대수

• 데이터를 분석하여 유용한 정보를 알아내거나 특징 공간을 변환하는 등의 과업을 수행하는 데 핵심 역할
• 학습 모델의 매개변수집합, 데이터, 선형연산의 결합 등을 행렬 또는 텐서로 간결하게 표현

벡터(Vector)

• 샘플을 특징 벡터(feature vector)로 표현
• 예) Iris 데이터에서 꽃받침의 길이, 꽃받침의 너비, 꽃잎의 길이, 꽃잎의 너비라는 4가지 특징이 각각 5.1, 3.5, 1.4, 0.2인 샘플

$$ \mathbf{x}=\begin{pmatrix}x_1 \\ x_2 \\ x_3 \\ x_4\end{pmatrix} = \begin{pmatrix}5.1 \\ 3.5 \\ 1.4 \\ 0.2\end{pmatrix}$$

$$ x=\begin{pmatrix}x_1 \\ x_2 \\ x_3 \\ x_4\end{pmatrix}=\begin{pmatrix}5.1 \\ 3.5 \\ 1.4 \\ 0.2\end{pmatrix} $$

행렬(Matrix)

• 여러 개의 벡터를 담는다.
• 훈련집합을 담은 행렬을 설계행렬이라 부른다.
• 예) Iris 데이터에 있는 150개의 샘플

$$\mathbf{X} = \begin{pmatrix} x_{1,1} & x_{1,2} & x_{1,3} & x_{1,4} \\ x_{2,1} & x_{2,2} & x_{2,3} & x_{2,4} \\ \vdots & \vdots & \vdots & \vdots \\ x_{150,1} & x_{150,2} & x_{150,3} & x_{150,4} \end{pmatrix}$$

텐서(tensor)

• 3차원 이상의 구조를 가진 숫자 배영
• 예) 3차원 구조의 RPG 컬러 영

놈(Norm)과 유사도

• 1차 놈은 $L_1 norm$, 맨해튼 놈 이라고도 불리고, 성분의 절대값의 합이다.
• 2차 놈은 $L_2 norm$, 유클리드 놈 이라고도 불리고, 가장 널리 쓰인다. 성분 제곱의 합의 루트이다.

$$\displaystyle\begin{Vmatrix}\mathbf{x}\end{Vmatrix}_\infty=\begin{pmatrix}\displaystyle\sum_{i=1}^{d}{\begin{vmatrix}x_i\end{vmatrix}^p}\end{pmatrix}^{\frac{1}{p}}$$

• 최대 놈은 $L_{\infty} norm$이며 성분들의 정대값 중에서 가장 큰 값으로 계산된다.

$$\begin{Vmatrix}\mathbf{x}\end{Vmatrix}_{\infty}=max(|x_1|,|x_2|,\dots,|x_d|)$$

• 행렬의 프로베니우스 놈

$$\begin{Vmatrix}\mathbf{A}\end{Vmatrix}_{F}=\displaystyle\begin{pmatrix}\displaystyle\sum_{i=1}^{n}\sum_{j=1}^{m}a_{ij}^2\end{pmatrix}^\frac{1}{2}$$

• 코사인 유사도
  • 내적공간의 두 벡터간 각도의 코사인값을 이용하여 벡터간의 유사한 정도를 의미한다.
  • 다차원의 양수 공간에서의 유사도 측정에 자주 이용한다.

$$\text{cosie similarity}(\mathbf{a,b})=\frac{\mathbf{a}}{\begin{Vmatrix}\mathbf{a}\end{Vmatrix}}\cdot\frac{\mathbf{b}}{\begin{Vmatrix}\mathbf{b}\end{Vmatrix}}=\cos{\theta}$$

퍼셉트론(Perceptron)

• 인공신경망의 한 종류이다.
  

• 퍼셉트론의 동작을 수식으로 표현

$$o=\tau(\mathbf{w\cdot x})=\begin{cases}1,a\geq T\\ -1,a< T\end{cases}$$

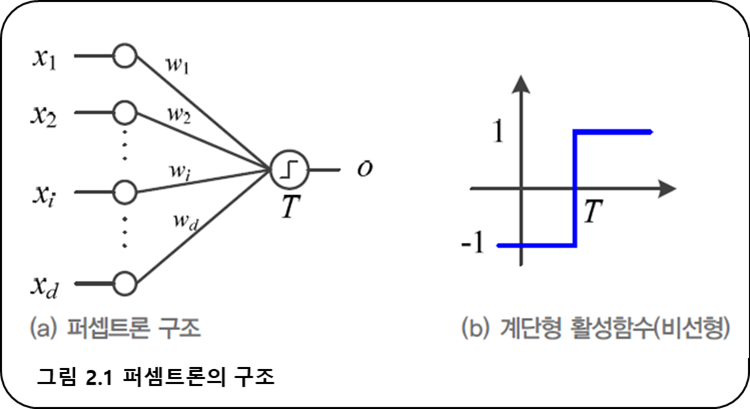
• 출력이 여러 개인 퍼셉트론
  • J번째 퍼셉트론의 가중치 벡터( $\mathbf{w}$ )와 출력벡터( $\mathbf{o}$ )

$$\mathbf{w}_j=(w_{j1},w_{j1},\dots,w_{jd})$$

$$\mathbf{o}=(o_1,o_2,\dots,o_e)^T$$

*동작을 수식으로 표현.

$$\mathbf{o}=\tau\begin{pmatrix}\mathbf{w}_1\cdot\mathbf{x} \\ \mathbf{w}_2\cdot\mathbf{x} \\ \vdots \\ \mathbf{w}_c\cdot\mathbf{x}\end{pmatrix}$$

• 가중치 벡터를 각 부류의 기준 벡터로 간주하면, c개의 부류의 유사도를 계산.

역행렬

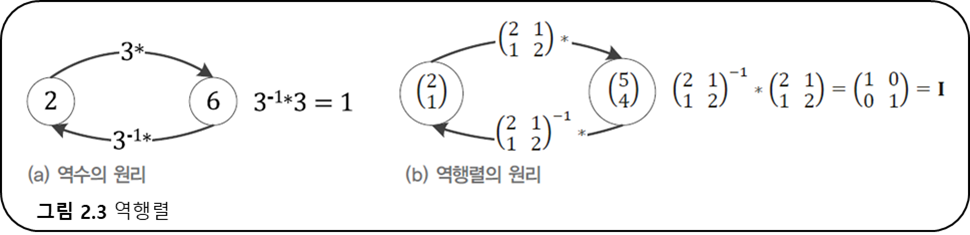
• 역행렬의 원리

• 역행렬이 존재하는 필요충분조건
  • 최대계수를 가진다.
  • 모든 행과 열이 선형독립이다.
  • 행렬식은 0이 아니다.
  • $\mathbf{A}^T\mathbf{A}$는 양의 정부호 대칭 행렬이다.
  • 고윳값은 모두 0이 아니다.

행렬 분해

• 고유 벡터( $\mathbf{v}$ )와 고윳값( $\lambda$ )

$$\mathbf{Av}=\lambda\mathbf{v}$$

• 고윳값 분해
  • $\mathbf{Q}$는 $\mathbf{A}$의 고유 벡터를 열에 배치한 행렬, $\Lambda$는 고윳값을 대각선에 배치한 대각행렬

$$\mathbf{A}=\mathbf{Q}\Lambda\mathbf{Q}^{-1}$$

• 특이값 분해
  • 왼쪽 특이행렬 $\mathbf{U}$는 $\mathbf{A}\mathbf{A}^T$의 고유 벡터를 열에 배치한 $n\times n$행렬
  • 오른쪽 특이행렬 $\mathbf{V}$는 $\mathbf{A}^T\mathbf{A}$의 고유 벡터를 열에 배치한 $m\times m$행렬
  • $\Sigma$는 $\mathbf{A}\mathbf{A}^T$의 고윳값의 제곱근을 대각선에 배치한 $n\times m$대각행렬

$$\mathbf{A}=\mathbf{U}\Sigma\mathbf{V}^T$$

Chapter 2.2 : 확률(Probability)과 통계

• 확률 : 어떤 일이 일어날 가능성을 측량하는 단위로 비율이나 빈도를 나타낸다.
• 통계 : 한 곳에 몰아서 어림잡아 계산한다.

확률(Probability)

$$P(\text{도})=\frac{4}{16},P(\text{개})=\frac{6}{16},P(\text{걸})=\frac{4}{16},P(\text{윷})=\frac{1}{16},P(\text{모})=\frac{1}{16}$$

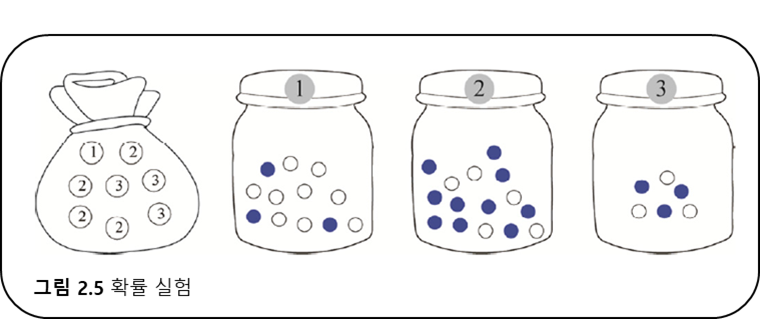
• 번호를 $y$, 공의 색을 $x$라는 확률변수로 표현하면 정의역은

$$y\in \begin{Bmatrix}\text{1, 2, 3}\end{Bmatrix}, x\in \begin{Bmatrix}\text{파랑, 하양}\end{Bmatrix}$$

• 카드가 1번, 공이 하양일 확률을 결합확률이라 한다.

$$P(y=\text{1},x=\text{하양})=P(x=\text{하양}|y=\text{1})P(y=\text{1})=\frac{9}{12}\frac{1}{8}=\frac{3}{32}$$

• 곱 규칙 : $P(y,x)=P(x|y)P(y)$
• 합 규칙 : $P(x)=\sum_{y} P(y,x)=\sum_{y} P(x|y)P(y)$
• 하양 공이 뽑힐 확률

$$P(\text{하양})=P(\text{하양}|\text{1})P(\text{1})+P(\text{하양}|\text{2})P(\text{2})+P(\text{하양}|\text{3})P(\text{3})$$

$$=\frac{9}{12}\frac{1}{8}+\frac{5}{15}\frac{4}{8}+\frac{3}{6}\frac{3}{8}=\frac{43}{96}$$

베이즈 정리(Bayes' theorem)

$$P(y|x)=\frac{P(x|y)P(y)}{P(x)}$$

• 위 실험에서 하양 공이 나왔다는 사실을 알고 어느 병에서 나온 공인지 추정.

$$\hat y=\operatorname*{arg\max}_yP(y|x=\text{하양})=\operatorname*{arg\max}_y\frac{P(x=\text{하양}|y)P(y)}{P(x=\text{하양})}$$

$$P(1|\text{하양})=\frac{P(\text{하양}|1)P(1)}{P(\text{하양})}=\frac{9}{43}$$

$$P(2|\text{하양})=\frac{P(\text{하양}|2)P(2)}{P(\text{하양})}=\frac{16}{43}$$

$$P(3|\text{하양})=\frac{P(\text{하양}|3)P(3)}{P(\text{하양})}=\frac{18}{43}$$

위로 가기