This C++ code is an improvement over the previous C++ code Nbody.cpp. Outside of making the code object oriented, this code implements an octree structure to organize all the bodies in the simulation, allowing for some approximations that vastly cut down on the run time. The Velocity-Verlet algorithm is still used, as well as Newtonian gravity and elastic collision detection. Thanks to massive improvements in memory usage however, this code is capable of handling hundreds or thousands of bodies over tens or hundreds of thousands of timesteps, with a runtime on order of a few seconds to an hour. The Barnes-Hut Octree structure and approximations implemented additionally allows for the runtime to scale as O(NlogN) as opposed to O(N^2).
This code is fully object oriented. There are several classes and one struct declated (which will be elaborated on further down) but the entire simulation is run within the bodygen object. The user-accessible main.cpp file only allows the user to run the simulation given a set of command line inputs.
This code is split into a header .hpp file and two .cpp files: bodygen.hpp, bodygen.cpp, main.cpp
- bodygen.hpp contains all the classes and structs, as well as all the function declarations within the classes
- bodygen.cpp contains all the function definitions, as well as various operator overloads
- main.cpp takes in command line inputs, checks for the correct inputs, and runs the simulation based on those inputs
The primary innovation of this code is the implementation of the Barnes-Hut Algorithm. For small scale simulations this does not provide many advantages, but for a large number of bodies, this algorithm is highly efficient in cutting down run time while still producing relatively accurate results.
The data structure to implement the algorithm comes in the form of a tree. The simulation space is divided into eight quadrants, with each of the eight quadrants then being subdivided further into eight subquadrants. This would then repeat recursively. Each quadrant or region can be considered a node that has eight branches, which are connected to the eight subregions or subquadrants, which themselves are nodes.
Suppose the simulation space is populated with a distribution of bodies. The Octree is created recursively such that there will be one body per leaf node. The attached image provides a simplified 2D version with a few bodies, but it can be generalized to 3D with many more bodies
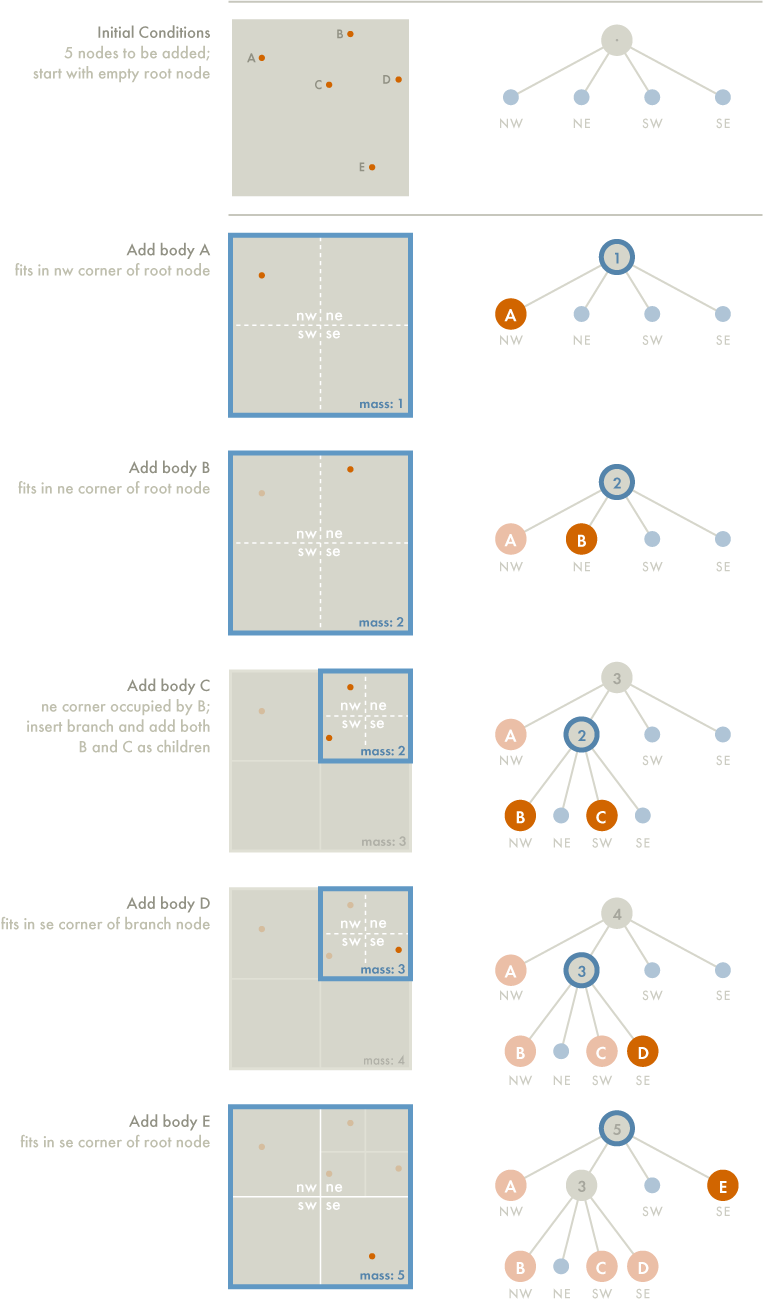
Each node would store the center of gravity, total mass and extent (or spread) of all bodies within that node, as well as point to eight child nodes.
With the structure in place, we can now apply the algorithm. The general idea is that if a collection of bodies are far enough away and span a small enough angular size, we can assume that collection of bodies to be a point mass at their center of gravity, and compute gravity from that point mass. This means instead of summing the gravitational vectors from each body in that collection, we have a single gravitational vector from the center of gravity. This massively speeds up the simulation speed, without too much loss in accuracy.
The more detailed steps are as follows. Suppose we have reached a leaf node with a single body, and wish to update it's acceleration. We are recusively iterating through the tree and have arrived at a node
-
We check if our leaf node is a descendant of the node. If so we check its child nodes for the same conditions. Once we've found a node that is not an ancestor of our leaf node, we can continue
-
If our node ends up being another leaf node, the gravitational vector is computed directly for our leaf node.
-
We look at the ratio between the extent of the bodies within the node and the distance between the node and our leaf node. You can think of this ratio as an angular diameter. If this ratio is greater than some predetermined value, we check the child nodes, and their children recursively.
-
If the ratio is less than the predetermined value, we stop at that node. We assume that node to be a point mass at its center of gravity, with the total mass of all bodies within that node, and calculate the gravitational vector.
In a worst case scenario, only steps 1 and 2 will be done, meaning that for each of the N bodies, we will have to iterate over the remaining N-1 bodies for a total of O(N^2) calculations. However generally, searching through a tree requires O(logN) calculations, meaning the overall big-O of the Barnes-Hut Algorithm is O(NlogN).
For small collections of bodies, this algorithm provides little measurable improvements over a standard O(N^2) simulation. But once we have thousands or more bodies, this algorithm provides a substantial run time improvement - a tenfold increase in the number of simulated bodies will not equate to a hundredfold increase in runtime. Below is a table across 1000 iterations of this code, comparing the body count to run time.
| Bodies | Runtime (s) |
|---|---|
| 10 | 0.0256581 |
| 50 | 0.160065 |
| 100 | 0.514786 |
| 400 | 4.57545 |
| 1000 | 21.0741 |
| 10000 | 752.019 |
As we can see, going from 10 to 50 bodies resulted in the runtime increasing by a factor of 8 as opposed to 25. From 10 to 100 bodies we see an increase by a factor of around 20 as opposed to 100.
This code employs the velocity-verlet algorithm to solve for position and velocity. I have attached a writeup of my previous Nbody.cpp code which discusses velocity-verlet in more detail, but mathematically the algorithm is expressed as follows
Now let us discuss the code itself. In bodygen.hpp, various objects are defined.
class body
{
public:
array<long double, 3> position, velocity, acceleration, newacceleration;
long double mass, radius;
int index;
};
class region
{
public:
array<long double, 2> xrange, yrange, zrange;
vector<body> bodiesinregion;
string regnodepath;
bool checkcol;
};
The body and region classes are relatively trivial so you can refer to the Doxygen documentation for all the details. In a nutshell body contains all the physical parameters of a body such as position, velocity, acceleration etc. Region contains the boundaries of a region or quadrant as well as bodiesinregion - a vector object that stores the bodies within that region.
Node is a struct that is the main data structure required to make the octree - in fact the node struct is the octree.
struct Node
{
bool isleaf;
string nodepath;
array<long double,3> cog;
long double cogmass;
long double extent;
body solebody;
array<Node*,8> Nodelist;
};Let us discuss the individual objects in the struct
isleafis a simple boolean true/false variable that is true only if the current node is a leaf.nodepathis a string that stores the path to the current node from the root node (the first node that represents the entire simulation space).cogstores the center of gravity of a given node - it is a length-3 array. In a physics/math sense this would be a vector.cogmassstores the total mass of the node, which is the masses of all bodies within this node and all of its descendants.extentstores the "spread" of the bodies in a node. This will be calculated in a function described later, but essentially is twice the average distance between all bodies and the center of gravity.solebodystores the body in the current node. This variable is only initialized and referenced ifisleaf == true. For non-leaf nodes, this variable stores junk data.Nodeliststores pointers to eight other nodes. This is the main definition that makes the Octree exist.
class Spacetree
{
public:
Spacetree(region);
Node* treegen();
private:
region regi;
Node* addnulls(Node*);
Node* makeatree(region);
vector<body> updatecollision(vector<body> &);
vector<body> mergebodies(vector<body> &);
};
This class simply makes the tree. The Spacetree(region) constructor initializes regi to some input region object. The functions will be discussed in detail further down, but in a nutshell treegen() makes a tree given regi, and the remaining functions help in making the tree. Most of the functions and regi are protected, with only the constructor and treegen publicly accessible.
This is the main class through which all the code is ran.
class bodygen
{
private:
Node* update(Node*);
Node* makebodies();
Node* updatesingleacceleration(Node*, Node*);
Node* updateallacceleration(Node*, Node*);
void deletetree(Node*);
bool comparetree(Node*, Node*);
array<long double,6> calcminmax();
array<long double,2> randcircgen(long double, long double);
array<long double,3> randspheregen(long double, long double);
size_t count{100};
string filename;
long double timestep{1};
size_t iterations{100};
Node* datatree;
region space;
bool writeinitfile;
vector<body> bodyvector;
public:
bodygen(string, long double, size_t);
bodygen(size_t, string, long double, size_t);
void simulate();
};
There are two constructors - bodygen(string, long double, size_t) is called when there is an initial data file to read, in which case filename is initialized to the desired file name. bodygen(size_t, string, long double, size_t) is called when there is no initial data file. In this case filename is initialized as a desired initial data file as the code generates the initial data, while the first size_t refers to the number of bodies to simulate, initialized to count. The remaining long double and size_t refer to the timestep and number of iterations, which are initialized to timestep and iterations respectively.
As for the remaining objects
datatreestores the octreespacestores the simulation spacewriteinitfileis a bool that determines if the code needs to generate bodies internallybodyvectorstores the information of all the bodies in a singlevectorobject
The remaining functions and helper functions will be discussed further down. As with the other classes, most of the variables and functions are protected, with only the constructors and the simulate function being publicly accessible.
The bodygen.cpp file contains all the object-oriented functions, in addition to all the necessary operator overloads.
First let us examine some standard operator overloads
template <typename T, size_t L>
array<T,L> operator+(const array<T,L> &v1, const array<T,L> &v2)
{
array<T,L> sum;
for(size_t i{0}; i < L; i++)
{
sum[i] = v1[i] + v2[i];
}
return(sum);
}
template <typename T, size_t L>
array<T,L> operator-(const array<T,L> &v1, const array<T,L> &v2)
{
array<T,L> sum;
for(size_t i{0}; i < L; i++)
{
sum[i] = v1[i] - v2[i];
}
return(sum);
}
template <typename T, size_t L>
T operator*(const array<T,L> &v1, const array<T,L> &v2)
{
T sum{0};
for(size_t i{0}; i < L; i++)
{
sum = sum + v1[i]*v2[i];
}
return(sum);
}
template <typename T, size_t L>
array<T,L> operator*(const T &s, array<T,L> &v)
{
array<T,L> returnval;
for(size_t i{0}; i < L; i++)
{
returnval[i] = s*v[i];
}
return(returnval);
}
These overloads are trivial vector algebra operations. The first two add or subtract vectors (in this case they are length L array objects of type T), the third is a dot product, and the fourth multiplies a scalar to a vector.
Next we have a series of more specialized operator overloads
template <typename T, size_t L>
bool operator>=(const array<T,L> &v1, const array<T,L> &v2)
{
for(size_t i{0}; i < L; i++)
{
if(v1[i] >= v2[i])
{
continue;
}
else
{
return(false);
}
}
return(true);
}
template <typename T, size_t L>
bool operator<(const array<T,L> &v1, const array<T,L> &v2)
{
for(size_t i{0}; i < L; i++)
{
if(v1[i] < v2[i])
{
continue;
}
else
{
return(false);
}
}
return(true);
}
bool operator==(const string &a, const string &b)
{
for(size_t i{0}; i < a.size(); i++)
{
if(a[i] != b[i])
{
return(false);
}
}
return(true);
}
ostream &operator<<(ostream &out, body &b)
{
out << b.index << ',';
for(size_t i{0}; i < 3; i++)
{
out << b.position[i] << ',';
}
for(size_t j{0}; j < 3; j++)
{
out << b.velocity[j] << ',';
}
out << b.mass << ',' << b.radius;
return(out);
}
ostream &operator<<(ostream &out, vector<body> &v)
{
out << "x coord" << ',' << "y coord" << ',' << "z coord" << ',' << "scalar\n";
for(size_t i{0}; i < v.size(); i++)
{
out << v[i].position[0] << ',' << v[i].position[1] << ',' << v[i].position[2] << ',' << v[i].radius << '\n';
}
return(out);
}
The first two overloads for >= and < take two 'array' objects of length L and compares their elements. If all comparisons are satisfied true is returned, otherwise false is returned. The third overload == compares two strings to determine if they are equal.
The last two overload the ostream operator <<. The first of these prints out the index, position, velocity, mass and radius of a body, while the second prints out the position and radius of every body in the vector object reference &v.
Two separate << overloads are defined here since they are used in different situations. The first is used to write out initial condition data, where velocity and mass are relevant, while the second writes out the simulation data, where those variables are not relevant for visualization.
Below are a series of minor helper functions that are not strictly tied to any class
template <typename T, size_t L>
T moodulus(const array<T,L> &v)
{
T sum{0};
for(size_t i{0}; i < v.size(); i++)
{
sum = sum + v[i]*v[i];
}
return(sqrt(sum));
}
template <typename T>
int sgn(T val)
{
return (T(0) < val) - (val < T(0));
}
template <typename T>
array<T,3> crossprod(array<T,3> &v1, array<T,3> &v2)
{
array<T,3> result = {v1[1]*v2[2] - v1[2]*v2[1], v1[2]*v2[0] - v1[0]*v2[2], v1[0]*v2[1] - v1[1]*v2[0]};
return(result);
}
The function moodulus outputs the length, or modulus, of some physical vector (in this instance it is an array of length L).
The function sgn returns the sign of some input of type T.
The function crossprod takes the vector cross product of two input vectors (in this instance they are array objects of length 3)
Spacetree has the following constructor
Spacetree::Spacetree(region inputreg)
: regi{inputreg} {}
which initializes regi to inputreg
Node* Spacetree::treegen()
{
Node* root = new Node;
regi.checkcol = false;
root = makeatree(regi);
return(root);
}
The only public function accessible in Spacetree. This function allocates memory for a new Node* pointer object and runs the makeatree function, which makes the octree. The regi.checkcol = false is inserted to initialize checkcol to false. checkcol is a parameter meant to check if collisions have already been calculated within a region/node. Will be elaborated further down
Node* Spacetree::addnulls(Node* newnode)
{
for(size_t i{0}; i < 8; i++)
{
newnode->Nodelist[i] = NULL;
}
return(newnode);
}
This function is only called on leaf nodes, and simply sets the leaf node to point to NULL pointers, terminating the tree.
vector<body> Spacetree::updatecollision(vector<body> &bodyvector)
{
vector<size_t> indices(0);
for(size_t i{0}; i < bodyvector.size(); i++)
{
for(size_t j{0}; j < bodyvector.size(); j++)
{
int check{0};
if(i == j)
{
continue;
}
for(size_t k{0}; k < indices.size(); k++)
{
if(i == indices[k] or j == indices[k])
{
check = 1;
break;
}
}
if(check == 1)
{
continue;
}
if(moodulus(bodyvector[i].position - bodyvector[j].position) < bodyvector[i].radius + bodyvector[j].radius)
{
const long double fact1 = (2*bodyvector[j].mass*((bodyvector[i].velocity - bodyvector[j].velocity)*(bodyvector[i].position - bodyvector[j].position))/((bodyvector[i].mass + bodyvector[j].mass)*moodulus(bodyvector[i].position - bodyvector[j].position)*moodulus(bodyvector[i].position - bodyvector[j].position)));
const long double fact2 = (2*bodyvector[i].mass*((bodyvector[j].velocity - bodyvector[i].velocity)*(bodyvector[j].position - bodyvector[i].position))/((bodyvector[i].mass + bodyvector[j].mass)*moodulus(bodyvector[i].position - bodyvector[j].position)*moodulus(bodyvector[i].position - bodyvector[j].position)));
array<long double, 3> posdiff1 = bodyvector[i].position - bodyvector[j].position;
array<long double, 3> posdiff2 = bodyvector[j].position - bodyvector[i].position;
bodyvector[i].velocity = bodyvector[i].velocity - fact1*posdiff1;
bodyvector[j].velocity = bodyvector[j].velocity - fact2*posdiff2;
indices.push_back(i);
indices.push_back(j);
}
}
}
return(bodyvector);
}
This function implements a standard collision check in a vector of body: bodyvector. bodyvector is looped over twice as each body is checked with each other. However if two bodies do collide, their indices are added to an indices vector object, and if those indices are encountered again, they will be skipped. This guarantees that only two bodies can collide with each other at each timestep.
The formula used to compute the collisions is below - for simplicity, all collisions are assumed to be elastic
Node* Spacetree::makeatree(region reg)
{
Node* pointer = new Node;
pointer->nodepath = reg.regnodepath;
if(reg.bodiesinregion.size() == 1)
{
pointer = addnulls(pointer);
pointer->isleaf = true;
pointer->solebody = reg.bodiesinregion[0];
pointer->cog = pointer->solebody.position;
pointer->cogmass = pointer->solebody.mass;
pointer->extent = 0;
return(pointer);
}
pointer->isleaf = false;
long double totmass{0};
long double extent{0};
array<long double, 3> tempcog = {0,0,0};
vector<body> regbods = reg.bodiesinregion;
long double maxrad{0};
for(size_t h{0}; h < regbods.size(); h++)
{
totmass = totmass + regbods[h].mass;
if(regbods[h].radius > maxrad)
{
maxrad = regbods[h].radius;
}
}
for(size_t hh{0}; hh < regbods.size(); hh++)
{
tempcog = tempcog + ((regbods[hh].mass)/(totmass))*regbods[hh].position;
}
for(size_t hhh{0}; hhh < regbods.size(); hhh++)
{
extent = extent + moodulus(regbods[hhh].position - tempcog);
}
pointer->cogmass = totmass;
pointer->cog = tempcog;
pointer->extent = 2*extent/regbods.size();
if(2*extent/regbods.size() < 10*maxrad && !reg.checkcol)
{
reg.bodiesinregion = updatecollision(reg.bodiesinregion);
reg.checkcol = true;
}
long double xboxlength = (reg.xrange[1] - reg.xrange[0])/2;
long double yboxlength = (reg.yrange[1] - reg.yrange[0])/2;
long double zboxlength = (reg.zrange[1] - reg.zrange[0])/2;
array<region,8> regionlist;
array<string,8> pathnames = {"dll","dlr","dal","dar","ull","ulr","ual","uar"};
regionlist[0].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[0].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[0].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[7].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[7].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[7].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
regionlist[1].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[1].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[1].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[2].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[2].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[2].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[3].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[3].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[3].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[4].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[4].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[4].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
regionlist[5].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[5].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[5].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
regionlist[6].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[6].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[6].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
for(size_t i{0}; i < 8; i++)
{
vector<body> newbodiesinregion(0);
regionlist[i].bodiesinregion = newbodiesinregion;
regionlist[i].regnodepath = reg.regnodepath + pathnames[i];
array<long double, 3> minranges = {regionlist[i].xrange[0], regionlist[i].yrange[0], regionlist[i].zrange[0]};
array<long double, 3> maxranges = {regionlist[i].xrange[1], regionlist[i].yrange[1], regionlist[i].zrange[1]};
for(size_t j{0}; j < reg.bodiesinregion.size(); j++)
{
if (reg.bodiesinregion[j].position >= minranges && reg.bodiesinregion[j].position < maxranges)
{
regionlist[i].bodiesinregion.push_back(reg.bodiesinregion[j]);
}
else
{
continue;
}
}
if(regionlist[i].bodiesinregion.size() >= 1)
{
if(reg.checkcol)
{
regionlist[i].checkcol = true;
}
else
{
regionlist[i].checkcol = false;
}
pointer->Nodelist[i] = makeatree(regionlist[i]);
}
else if(regionlist[i].bodiesinregion.size() == 0)
{
pointer->Nodelist[i] = NULL;
}
}
return(pointer);
}
This function is quite long so let us walk through the function step by step
Node* pointer = new Node;
pointer->nodepath = reg.regnodepath;
if(reg.bodiesinregion.size() == 1)
{
pointer = addnulls(pointer);
pointer->isleaf = true;
pointer->solebody = reg.bodiesinregion[0];
pointer->cog = pointer->solebody.position;
pointer->cogmass = pointer->solebody.mass;
pointer->extent = 0;
return(pointer);
}
pointer->isleaf = false;
First new memory is allocated for a new Node* pointer. The next line sets the nodepath to reg.regnodepath. This is done since this function makeatree is called recursively with region as its argument, so information on the path must be stored in the region object as the tree is created recursively, with it being stored in the node at this step. The if statement checks if there is only one body in this region - if so, isleaf is set to true, NULL pointers are added to the Nodelist of the current node, and the solebody is updated to be the one remaining body (along with some other assignments such as assigning cog to simply be the position of the body). This check is necessary since we want to terminate the tree when there is one body remaining - we do not want a situation where the tree continues branching into smaller and smaller quadrants containing that one body, eventually resulting in a memory leak.
long double totmass{0};
long double extent{0};
array<long double, 3> tempcog = {0,0,0};
vector<body> regbods = reg.bodiesinregion;
long double maxrad{0};
for(size_t h{0}; h < regbods.size(); h++)
{
totmass = totmass + regbods[h].mass;
if(regbods[h].radius > maxrad)
{
maxrad = regbods[h].radius;
}
}
for(size_t hh{0}; hh < regbods.size(); hh++)
{
tempcog = tempcog + ((regbods[hh].mass)/(totmass))*regbods[hh].position;
}
for(size_t hhh{0}; hhh < regbods.size(); hhh++)
{
extent = extent + moodulus(regbods[hhh].position - tempcog);
}
pointer->cogmass = totmass;
pointer->cog = tempcog;
pointer->extent = 2*extent/regbods.size();
This part of the function is relatively trivial. We loop through all the bodies in the current region to compute the center of gravity, total mass, and extent of the current node. I have defined the extent to be the average distance between each body and the center of gravity multiplied by two, and it characterizes the 'spread' of a group of bodies
if(2*extent/regbods.size() < 10*maxrad && !reg.checkcol)
{
reg.bodiesinregion = updatecollision(reg.bodiesinregion);
reg.checkcol = true;
}
This part of the function prevents the code from being O(N^2) since that is the big-O for updatecollision. This only applies updatecollision if the extent of the node is small enough (specifically, if the extent is less than 10 times the radius of the largest body). However, this piece of code is not entirely necessary. My implementation of collisions is relatively crude and requires small timesteps, and would likely fail for astronomical scales (one second timesteps are simply too small for astronomical simulations). The user can feel free to comment out this portion of the code if they so choose.
long double xboxlength = (reg.xrange[1] - reg.xrange[0])/2;
long double yboxlength = (reg.yrange[1] - reg.yrange[0])/2;
long double zboxlength = (reg.zrange[1] - reg.zrange[0])/2;
array<region,8> regionlist;
array<string,8> pathnames = {"dll","dlr","dal","dar","ull","ulr","ual","uar"};
regionlist[0].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[0].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[0].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[7].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[7].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[7].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
regionlist[1].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[1].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[1].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[2].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[2].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[2].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[3].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[3].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[3].zrange = {reg.zrange[0], reg.zrange[0] + zboxlength};
regionlist[4].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[4].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[4].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
regionlist[5].xrange = {reg.xrange[0]+xboxlength, reg.xrange[1]};
regionlist[5].yrange = {reg.yrange[0], reg.yrange[0] + yboxlength};
regionlist[5].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
regionlist[6].xrange = {reg.xrange[0], reg.xrange[0] + xboxlength};
regionlist[6].yrange = {reg.yrange[0]+yboxlength, reg.yrange[1]};
regionlist[6].zrange = {reg.zrange[0]+zboxlength, reg.zrange[1]};
This part of the function subdivides the current region into eight quadrants, which are stored in an array object regionlist, as well as the an array of labels pathnames. These labels will be added to the nodepath string, and act as simple labels for each of the quadrants.
for(size_t i{0}; i < 8; i++)
{
vector<body> newbodiesinregion(0);
regionlist[i].bodiesinregion = newbodiesinregion;
regionlist[i].regnodepath = reg.regnodepath + pathnames[i];
array<long double, 3> minranges = {regionlist[i].xrange[0], regionlist[i].yrange[0], regionlist[i].zrange[0]};
array<long double, 3> maxranges = {regionlist[i].xrange[1], regionlist[i].yrange[1], regionlist[i].zrange[1]};
for(size_t j{0}; j < reg.bodiesinregion.size(); j++)
{
if (reg.bodiesinregion[j].position >= minranges && reg.bodiesinregion[j].position < maxranges)
{
regionlist[i].bodiesinregion.push_back(reg.bodiesinregion[j]);
}
else
{
continue;
}
}
if(regionlist[i].bodiesinregion.size() >= 1)
{
if(reg.checkcol)
{
regionlist[i].checkcol = true;
}
else
{
regionlist[i].checkcol = false;
}
pointer->Nodelist[i] = makeatree(regionlist[i]);
}
else if(regionlist[i].bodiesinregion.size() == 0)
{
pointer->Nodelist[i] = NULL;
}
}
return(pointer);
The final part of the function does two things within a loop over regionlist. First, bodies in reg.bodiesinregion are assigned to one of the eight quadrants if they fall within one of them. Second, the makeatree function is called recursively on each element in regionlist for each element in pointer->Nodelist. Also if updatecollision was ran earlier and checkcol is set to true, it will be set to true for all sub regions. Finally, for elements in regionlist with no bodies, the corresponding element in pointer->Nodelist is set to point to NULL.
bodygen has two constructors
bodygen::bodygen(const string inputstring, long double tstepinput, const size_t iter)
: filename{inputstring}, timestep{tstepinput}, iterations{iter}
{
bodyvector.resize(0);
writeinitfile = false;
}
bodygen::bodygen(const size_t inputcount, const string st, long double tstepinput, const size_t iter)
: count{inputcount}, filename{st}, timestep{tstepinput}, iterations{iter}
{
bodyvector.resize(0);
writeinitfile = true;
}
The first constructor initializes filename to inputstring, timestep to tstepinput and iterations to iter. Additionally writeinitfile is set to false. This constructor is called when there is an existing initial data file to be read. filename in this case refers to the desired filename to be read.
The second constructor initializes count to inputcount, filename to st, timestep to tstepinput and iterations to iter. Additionally writeinitfile is set to true. This constructor is called when there is no existing initial data file to be read, and the user wants to generate new data. filename in this case refers to the filename the user wishes to name the generated initial data file
void bodygen::deletetree(Node* tree)
{
if(tree == NULL)
{
return;
}
for(size_t i{0}; i < 8; i++)
{
deletetree(tree->Nodelist[i]);
}
delete tree;
}
This function is relatively trivial - it recursively deletes all nodes within a tree and frees up the memory
This is the main function that runs the simulation
void bodygen::simulate()
{
if(writeinitfile)
{
datatree = makebodies(); //Make bodies if theres no initial data file
}
else
{
string infolist[8];
string radiuss;
ifstream file(filename); //Opens initial data file
array<long double, 6> minmax = {0,0,0,0,0,0};
int previndex{-1};
while(file.is_open() == true)
{
body newbody;
for(size_t i{0}; i < 8; i++)
{
getline(file, infolist[i], ',');
}
getline(file, radiuss, '\n');
if(stoi(infolist[0]) == previndex)
{
break;
}
newbody.index = stoi(infolist[0]);
newbody.position = {stold(infolist[1]),stold(infolist[2]),stold(infolist[3])};
newbody.velocity = {stold(infolist[4]),stold(infolist[5]),stold(infolist[6])};
newbody.mass = stold(infolist[7]);
newbody.radius = stold(radiuss);
newbody.acceleration = {0,0,0};
newbody.newacceleration = {0,0,0};
bodyvector.push_back(newbody);
previndex = newbody.index;
size_t k2{0};
for(size_t k{0}; k < 3; k++)
{
if(newbody.position[k] < minmax[k2])
{
minmax[k2] = newbody.position[k];
}
else if(newbody.position[k] > minmax[k2+1])
{
minmax[k2+1] = newbody.position[k];
}
k2 = k2 + 2;
}
}
file.close();
space.xrange = {minmax[0] - 1,minmax[1] + 1};
space.yrange = {minmax[2] - 1,minmax[3] + 1};
space.zrange = {minmax[4] - 1,minmax[5] + 1};
space.bodiesinregion = bodyvector;
Spacetree space_tree{space};
datatree = space_tree.treegen();
}
string strdirname = filename.substr(0, filename.size()-4);
const char* dirname = strdirname.c_str();
mkdir(dirname);
array<long double,6> minimaxi;
size_t j{0};
int ccount{0};
for(size_t i{0}; i < iterations; i++)
{
datatree = updateallacceleration(datatree, datatree);
datatree = update(datatree);
if(j == 100)
{
ofstream datafile;
datafile.precision(30);
filename = ".\\" + strdirname + "\\" + strdirname + ".csv." + to_string(ccount);
datafile.open(filename);
datafile << fixed << bodyvector;
datafile.close();
j = 0;
ccount = ccount + 1;
}
minimaxi = calcminmax();
space.xrange = {minimaxi[0] - 1,minimaxi[1] + 1};
space.yrange = {minimaxi[2] - 1,minimaxi[3] + 1};
space.zrange = {minimaxi[4] - 1,minimaxi[5] + 1};
space.bodiesinregion = bodyvector;
Spacetree space_tree{space};
deletetree(datatree);
datatree = space_tree.treegen();
j = j + 1;
}
}
This function is quite long but it is relatively straightforward. Nonetheless let us break it down into pieces
if(writeinitfile)
{
datatree = makebodies(); //Make bodies if theres no initial data file
}
else
{
string infolist[8];
string radiuss;
ifstream file(filename); //Opens initial data file
array<long double, 6> minmax = {0,0,0,0,0,0};
int previndex{-1};
while(file.is_open() == true)
{
body newbody;
for(size_t i{0}; i < 8; i++)
{
getline(file, infolist[i], ',');
}
getline(file, radiuss, '\n');
if(stoi(infolist[0]) == previndex)
{
break;
}
newbody.index = stoi(infolist[0]);
newbody.position = {stold(infolist[1]),stold(infolist[2]),stold(infolist[3])};
newbody.velocity = {stold(infolist[4]),stold(infolist[5]),stold(infolist[6])};
newbody.mass = stold(infolist[7]);
newbody.radius = stold(radiuss);
newbody.acceleration = {0,0,0};
newbody.newacceleration = {0,0,0};
bodyvector.push_back(newbody);
previndex = newbody.index;
size_t k2{0};
for(size_t k{0}; k < 3; k++)
{
if(newbody.position[k] < minmax[k2])
{
minmax[k2] = newbody.position[k];
}
else if(newbody.position[k] > minmax[k2+1])
{
minmax[k2+1] = newbody.position[k];
}
k2 = k2 + 2;
}
}
file.close();
space.xrange = {minmax[0] - 1,minmax[1] + 1};
space.yrange = {minmax[2] - 1,minmax[3] + 1};
space.zrange = {minmax[4] - 1,minmax[5] + 1};
space.bodiesinregion = bodyvector;
Spacetree space_tree{space};
datatree = space_tree.treegen();
}
This if else statement checks if writeinitfile is true or false. If true, the function makebodies is called (to be discussed further below) and generates bodies. Otherwise, the data is read from filename into a vector of body objects, before datatree is created, containing those bodies.
string strdirname = filename.substr(0, filename.size()-4);
const char* dirname = strdirname.c_str();
mkdir(dirname);
array<long double,6> minimaxi;
size_t j{0};
int ccount{0};
for(size_t i{0}; i < iterations; i++)
{
datatree = updateallacceleration(datatree, datatree);
datatree = update(datatree);
if(j == 100)
{
ofstream datafile;
datafile.precision(30);
filename = ".\\" + strdirname + "\\" + strdirname + ".csv." + to_string(ccount);
datafile.open(filename);
datafile << fixed << bodyvector;
datafile.close();
j = 0;
ccount = ccount + 1;
}
minimaxi = calcminmax();
space.xrange = {minimaxi[0] - 1,minimaxi[1] + 1};
space.yrange = {minimaxi[2] - 1,minimaxi[3] + 1};
space.zrange = {minimaxi[4] - 1,minimaxi[5] + 1};
space.bodiesinregion = bodyvector;
Spacetree space_tree{space};
deletetree(datatree);
datatree = space_tree.treegen();
j = j + 1;
}
Here the actual simulation is ran. Outside the loop the main thing to note is the output file name will be whatever to input file name/initial data file name was + .csv at the end. So for instance, "data.csv" will be output as "dataNbody.csv". The actual output itself is non trivial however - a directory with the name filename is created, and the data is output as "dataNbody.csv.ccount" where ccount is an integer that tracks the index of the output data. For instance the 56th output with initial data file name data.csv would be written as "dataNbody.csv.55" ("dataNbody.csv.0" is the first).
Within the loop, the primary functions that are run are updateallacceleration and update (both to be explained further below), which updates the positions, velocities and acclerations of all bodies at the current timestep. The if(j == 100) part is written in so that only every 100th iteration is output into a data file - this was done to minimize the amount of space taken in the computer and helps with the visualization, but the user can remove the if statement if they wish to output data at every single timestep, or change the value. Below the loop, the bounds are recalculated, and datatree is deleted and then remade. datatree is remade at every timestep to maximize the accuracy of the simulation, given that moving bodies would drastically alter the structure of a tree over time.
array<long double,6> bodygen::calcminmax()
{
array<long double,6> minmax{0,0,0,0,0,0};
for(size_t i{0}; i < bodyvector.size(); i++)
{
size_t k2{0};
for(size_t k{0}; k < 3; k++)
{
if(bodyvector[i].position[k] < minmax[k2])
{
minmax[k2] = bodyvector[i].position[k];
}
else if(bodyvector[i].position[k] > minmax[k2+1])
{
minmax[k2+1] = bodyvector[i].position[k];
}
k2 = k2 + 2;
}
}
return(minmax);
}
This function calculates the boundaries of the smallest box that would encapsulate all body objects inside bodyvector. This is a helper function that makes it easy to create a new region.
array<long double,2> bodygen::randcircgen(long double r1, long double r2)
{
random_device rd;
mt19937_64 mt64(rd());
long double scale = ((long double) mt64())/((long double) mt64.max());
long double scale2 = ((long double) mt64())/((long double) mt64.max());
long double scale3 = ((long double) mt64())/((long double) mt64.max());
long double chosenr = r1 + (r2 - r1)*scale;
array<long double, 2> xd = {0,0};
xd[0] = (2*scale3 - 1)*chosenr;
xd[1] = sgn(2*scale2 - 1)*sqrt(chosenr*chosenr - xd[0]*xd[0]);
return(xd);
}
array<long double,3> bodygen::randspheregen(long double r1, long double r2)
{
random_device rd;
mt19937_64 mt64(rd());
long double scale = ((long double) mt64())/((long double) mt64.max());
long double scale2 = ((long double) mt64())/((long double) mt64.max());
long double scale3 = ((long double) mt64())/((long double) mt64.max());
long double scale4 = ((long double) mt64())/((long double) mt64.max());
long double chosenr = r1 + (r2 - r1)*scale;
array<long double, 3> xd = {0,0,0};
xd[0] = (2*scale2 - 1)*chosenr;
xd[1] = (2*scale3 - 1)*sqrt(chosenr*chosenr - xd[0]*xd[0]);
xd[2] = sgn(2*scale4 - 1)*sqrt(chosenr*chosenr - xd[0]*xd[0] - xd[1]*xd[1]);
return(xd);
}
These are two helper functions that generate either random 2D or 3D coordinates within some annulus or spherical shell of inner radius r1 and outer radius r2.
Node* bodygen::makebodies()
{
bodyvector.resize(count);
ofstream datafile;
datafile.precision(30);
datafile.open(filename);
array<long double, 8> randlist;
for(size_t i{0}; i < count; i++)
{
for(size_t j{0}; j < 8; j++)
{
random_device rd;
mt19937_64 mt64(rd());
randlist[j] = 2*((long double) mt64()/((long double) mt64.max())) - 1;
}
//array<long double,3> spherevars = randspheregen(10, 1E7);
//array<long double,2> circvars = randcircgen(1.2E9, 4E9);
//bodyvector[i].position = {spherevars[0], spherevars[1], spherevars[2]};
//bodyvector[i].position = {circvars[0], circvars[1], 1E5*randlist[2]};
//array<long double,3> randrotvec = {randlist[0],randlist[1],randlist[2]};
//randrotvec = (1/moodulus(randrotvec))*randrotvec;
//array<long double,3> perpvec = crossprod(bodyvector[i].position, randrotvec);
//perpvec = (1/moodulus(perpvec))*perpvec;
//const long double extrafactor = sqrt(G*1E30/(moodulus(bodyvector[i].position)))/moodulus(bodyvector[i].position);
//bodyvector[i].velocity = crossprod(bodyvector[i].position,perpvec);
//bodyvector[i].velocity = extrafactor*bodyvector[i].velocity;
bodyvector[i].position = {10E15*randlist[0], 10E15*randlist[1], 10E15*randlist[2]};
bodyvector[i].velocity = {1000*randlist[3], 1000*randlist[4], 1000*randlist[5]};
bodyvector[i].mass = 3E30*(randlist[6]+1)/2;
bodyvector[i].radius = 1E9*(randlist[7]+1)/2;
bodyvector[i].index = i;
if(i == count - 1)
{
/*
bodyvector[i].position = {0,0,0};
bodyvector[i].velocity = {0,0,0};
bodyvector[i].mass = 1E40;
bodyvector[i].radius = 0;
bodyvector[i].index = i;
*/
datafile << fixed << bodyvector[i];
}
else
{
datafile << fixed << bodyvector[i] << '\n';
}
}
datafile.close();
array<long double,6> minimaxi = calcminmax();
space.xrange = {minimaxi[0] - 1,minimaxi[1] + 1};
space.yrange = {minimaxi[2] - 1,minimaxi[3] + 1};
space.zrange = {minimaxi[4] - 1,minimaxi[5] + 1};
space.bodiesinregion = bodyvector;
Spacetree space_tree{space};
return(space_tree.treegen());
}
This function randomly generates count bodies. Upon immediate inspection you may notice various pieces of code have been commented out. I made the conscious choice to comment these sections out rather than delete them since these are examples of code I used to generate initial data which were used in some of the visualizations. The uncommented portion randomly generates bodies within a cube 10E15 meters in side length, but the user is encouraged to fiddle around and generate their own initial conditions.
The additional multiline comment below the if statement represents a central mass much greater than the other masses. I've included a central mass in all of my visualizations since without one the simulation looks quite boring.
Once the data is generated, it is assigned to bodyvector and written out to filename, before being placed into datatree.
bool bodygen::comparetree(Node* root, Node* tree)
{
if(root->nodepath == tree->nodepath)
{
return(true);
}
else
{
for(size_t i{0}; i < 8; i++)
{
if(tree->Nodelist[i] != NULL)
{
return(comparetree(root,tree->Nodelist[i]));
}
}
return(false);
}
}
This function is recursively called through tree, and at each step it checks if the nodepaths of root and tree are the same. It returns true if they are, false otherwise. In other words, this function checks if root is a descendant node of tree.
Node* bodygen::updateallacceleration(Node* tree, Node* wholetree)
{
if(tree == NULL)
{
return(tree);
}
if(tree->isleaf)
{
tree = updatesingleacceleration(tree,wholetree);
}
else
{
for(size_t i{0}; i < 8; i++)
{
tree->Nodelist[i] = updateallacceleration(tree->Nodelist[i],wholetree);
}
}
return(tree);
}
This function recursively updates the accelerations of all leaf nodes, applying recursion through tree. If tree is a leaf node, the function updatesingleacceleration is called.
Node* bodygen::updatesingleacceleration(Node* root, Node* tree)
{
if(tree == NULL)
{
return(root);
}
if(!comparetree(root,tree) && (tree->extent/(moodulus(root->solebody.position - tree->cog)) < 0.3 or tree->isleaf))
{
long double A = G*tree->cogmass/(moodulus(tree->cog - root->solebody.position)*moodulus(tree->cog - root->solebody.position)*moodulus(tree->cog - root->solebody.position));
array<long double,3> B = tree->cog - root->solebody.position;
root->solebody.newacceleration = root->solebody.newacceleration + A*B;
}
else
{
for(size_t i{0}; i < 8; i++)
{
root = updatesingleacceleration(root,tree->Nodelist[i]);
}
}
return(root);
}
This function is where the Barnes-Hut Algorithm is fully applied, encapsulated in the second if statement. If root is not a child node of tree and if the angular size (extent divided by distance) is less than 0.3 or if tree is a leaf node, then the gravitational pull of tree on root is calculated. If the appropriate conditions are not satisfied, the function is called recursively on the child nodes of tree.
Node* bodygen::update(Node* tree)
{
if(tree == NULL)
{
return(tree);
}
if(tree->isleaf)
{
array<long double,3> sumacc = tree->solebody.acceleration + tree->solebody.newacceleration;
tree->solebody.position = tree->solebody.position + timestep*tree->solebody.velocity + (0.5*timestep*timestep)*tree->solebody.acceleration;
tree->solebody.velocity = tree->solebody.velocity + (0.5*timestep)*sumacc;
tree->solebody.acceleration = tree->solebody.newacceleration;
tree->solebody.newacceleration = {0,0,0};
bodyvector[tree->solebody.index] = tree->solebody;
}
else
{
for(size_t i{0}; i < 8; i++)
{
tree->Nodelist[i] = update(tree->Nodelist[i]);
}
}
return(tree);
}
This function, like the ones before it, is recursive. It searches through tree and updates the positions and velocites of all leaf nodes. Additionally, the appropriate index in bodyvector is also updated, allowing for the tree to be deleted and then remade later without losing data.
Finally we have the main function.
int main(int argc, char* argv[])
{
chrono::time_point start_time{chrono::steady_clock::now()};
if(argc > 5 or argc < 4)
{
std::cout << "Incorrect number of inputs\n";
return 0;
}
else if(argc == 4)
{
for(size_t j{2}; j < 4; j++)
{
if((size_t) atoi(argv[j]) <= 0)
{
std::cout << "Invalid inputs detected - please input a positive integer, long double and postive integer, or a string, long double, and positive integer.\n";
return 0;
}
}
if((size_t) atoi(argv[1]) == 0)
{
ifstream file(argv[1]);
if(!file.is_open())
{
std::cout << "Input file not found\n";
return 0;
}
else
{
string str = (string) argv[1];
long double ld = (long double) atoi(argv[2]);
size_t st = (size_t) atoi(argv[3]);
bodygen gen{str,ld,st};
gen.simulate();
chrono::time_point end_time{chrono::steady_clock::now()};
chrono::duration<double> elapsed_time_seconds{end_time - start_time};
chrono::duration<double, milli> elapsed_time_milli{end_time - start_time};
cout << "Elapsed time: " << elapsed_time_seconds.count() << " seconds, ";
return 0;
}
}
}
else
{
for(size_t j{1}; j < 5; j++)
{
if((size_t) atoi(argv[j]) <= 0 && j != 2)
{
std::cout << "Invalid inputs detected - please input a positive integer, long double and postive integer, or a string, long double, and positive integer.\n";
return 0;
}
}
size_t st1 = (size_t) atoi(argv[1]);
string str = (string) argv[2];
long double ld = (long double) atoi(argv[3]);
size_t st = (size_t) atoi(argv[4]);
bodygen gen{st1,str,ld,st};
gen.simulate();
chrono::time_point end_time{chrono::steady_clock::now()};
chrono::duration<double> elapsed_time_seconds{end_time - start_time};
chrono::duration<double, milli> elapsed_time_milli{end_time - start_time};
cout << "Elapsed time: " << elapsed_time_seconds.count() << " seconds, ";
return 0;
}
}
The main function has many checks in place to make sure the command line inputs are correct. Error messages will be returned if there are insufficient/too many inputs, incorrect inputs (letters when in places where numbers are asked for, or negative numbers), or if a file is not found. There are two sets of possible command line inputs
C:\Filepath> ./bodygen.exe filename.csv positive_number positive_integerA possible input would be
C:\Filepath> ./bodygen.exe gg.csv 10 4600which would take the initial condition data gg.csv, and run 4600 iterations with 10 second timesteps, and output "ggNbody.csv" to the folder "gg".
C:\Filepath> ./bodygen.exe positive_integer filename.csv positive_number positive_integer
A possible input would be
C:\Filepath> ./bodygen.exe 500 balls.csv 1.6834 3555which would create an initial condition data file "balls.csv" with 500 bodies, simulate with 1.6834 second timesteps over 3555 iterations, and output to "ballsNbody.csv" to the folder "balls".
Included in the git repository are some sample data I have generated. "testdata.csv" and "gg.csv" are initial condition data files, and in the "testdata" and "gg" folders we find the corresponding simulated data sets.
The simulation data is written out in a way such that it can be read by Paraview. I've created five animations (which unfortunately I cannot upload to github, so instead I will include a google drive link below), all of which are 1000 bodies with a central mass.
https://drive.google.com/drive/folders/1KSQek9YFoXO6Z9lsXeq_I0boNn8Yz7W_?usp=sharing
To briefly describe each simulation
-
orbits.avi is simply a collection of asteroids orbiting some central mass with 100 second timesteps
-
orbitsdetailed.avi is a more accurate simulation of orbits.avi with 10 second timesteps.
-
testanim.avi is a simulation set where I messed up my initial conditions such that the bodies ended up in a half ring around the central mass, but it looked cool so I kept it
-
kepler.avi is a demonstration of kepler shear - how some "line" of mass gets distorted into a spiral
-
disruption.avi contains the same planetary ring/disk system from orbitsdetailed.avi but now I've included a massive body that interferes and disrupts the system by flying right into the disk


