기본적인 알고리즘 문제들을 함께 해결해보는 공간, NBA입니다.
- 양희제
-
김태학
-
박진성
-
이강윤
-
이기용
-
김도언
-
송대현
-
유덕균
-
조용현
Details
운영 계획
- 2023년 1월 변경사항 : 프로젝트 집중 기간으로, 알고리즘에 대한 감을 잃지 않기 위해 각자의 수준에 맞는 문제를 일주일에 최소 1문제 이상 자율적으로 해결합니다.
- ~~2022년 9월 변경사항 : 다양한 알고리즘 문제 사이트에 존재하는 IM형 문제(필수), A형 문제(선택)들을 일주일에 2~3문제(IM형 1~2문제, A형 1문제)씩 해결합니다.~~
- ~~2022년 8월 변경사항 : SWEA에 존재하는 D1, D2 문제(총 44문제)를 일주일에 5문제씩 해결합니다.~~
- 주어진 문제 중 각각 1문제씩 골라 회의 날짜에 발표합니다. 이 때, 관련 개념에 대해 함께 설명하여야 하며, 모든 팀원이 이해할 수 있도록 충분히 노력하여야 합니다.
- 해결한 문제들은 양식에 맞게 파일 내에 작성한 뒤 Github에 Push합니다.
- 관련 개념들은 정리하여 노션 페이지에 업로드합니다.
- 월말에 그동안의 회의를 토대로 팀원끼리 익명투표하여 참여우수 교육생을 선발합니다.
- 매월 참여우수 교육생은 월말 결과보고서에 우수 교육생 관련하여 이름이 기재될 예정입니다.
Details
팀원 규칙
🧡 시간 약속 잘 지키기!!
💚 팀원 간 쿠션어 사용하기!!(부드러운 말 사용)
💛 회의 시 발표 끝나면 박수 쳐주기!! 👏👏👏👏
Details
파일 네이밍 규칙 및 폴더 구조
- 파일 네이밍 규칙
- 매주 푼 문제를 자신의 폴더 안에
문제번호.py로 추가합니다. - 이 때, 코드 맨 위에 주석으로 문제 제목을 작성합니다.
- 예시(1545.py)
- 매주 푼 문제를 자신의 폴더 안에
- 폴더 구조
Details
커밋 메세지 규칙
- NBA Commit message 구조
- 원래 기본적으로 Commit message는 제목, 본문, 꼬리말로 구성되지만, 기초 알고리즘을 푸는 교육생임을 감안하여 제목만을 작성합니다.
- 위에서 언급한 제목은 커밋 명령어인
git commit -m "커밋 메세지"에서"커밋 메세지"를 뜻하며, 편의상 커밋 메세지라고 부르겠습니다. - 커밋 메세지는 다음과 같은 양식으로 작성합니다.
"<타입>: <내용>"
-
타입의 종류
- Feat: 알고리즘 문제 파일 추가 및 수정
- Docs: 주석 또는 README.md 내용 수정
- Refactor: 기능의 변화가 아닌 코드 리팩토링 ex) 변수 이름 변경
- 커밋 예시
- NBA Commit message 규칙
- 커밋 메세지는 50자 이내로 작성합니다.
- 커밋 메세지의 첫 글자는 대문자로 작성합니다.
- 제목은 명령문으로 작성하고, 과거형으로 작성하지 않습니다.
Details
관련 개념 정리
- 매주 해결하는 알고리즘 문제들과 관련된 개념들을 정리하여 업로드합니다.
- 관련 개념 정리 문서는 아래 위치한 세부 계획에 주 단위로 기록합니다.
| 이름 | 문제 | 풀이 |
|---|---|---|
| 유덕균 | [BOJ] 2012. 등수 매기기 | 바로가기 |
| 김도언 | [BOJ] 14889. 스타트와 링크 | 바로가기 |
| 이강윤 | [BOJ] 13335. 트럭 | 바로가기 |
| 이기용 | [BOJ] 1260. DFS와 BFS | 바로가기 |
| 양희제 | [BOJ] 14889. 스타트와 링크 | 바로가기 |
| 박진성 | [SWEA] 1244. 최대 상금 | 바로가기 |
| 이름 | 문제 | 풀이 |
|---|---|---|
| 유덕균 | [BOJ] 2755. 이번학기 평점은 몇점? | 바로가기 |
| 김도언 | [BOJ] 9020. 골드바흐의 추측 | 바로가기 |
| 이강윤 | [BOJ] 1748. 수 이어 쓰기 1 | 바로가기 |
| 양희제 | [BOJ] 4948. 베르트랑 공준 | 바로가기 |
| 박진성 | [BOJ] 15686. 치킨 배달 | 바로가기 |
| 조용현 | [BOJ] 14889. 스타트와 링크 | 바로가기 |
| 이름 | 문제 | 풀이 |
|---|---|---|
| 유덕균 | [Programmers] 120956. 옹알이 (1) | 바로가기 |
| 김도언 | [BOJ] 18870. 좌표 압축 | 바로가기 |
| 양희제 | [BOJ] 16928. 뱀과 사다리 게임 | 바로가기 |
| 조용현 | [BOJ] 2012. 등수 매기기 | 바로가기 |
| 문제 이름 | 난이도 | 발표자 및 풀이 |
|---|---|---|
| [Programmers] 72410. 신규 아이디 추천 | LV1 | 박진성 |
| [BOJ] 7569. 토마토(3차원) | G5 | 이기용 |
| [Programmers] 77485. 행렬 테두리 회전하기 | LV2 | 김도언, 양희제 |
| [BOJ] 2638. 치즈 | G3 | 이강윤, 김태학 |
| 문제 이름 | 난이도 | 발표자 및 풀이 |
|---|---|---|
| [Programmers] 42889. 실패율 | LV1 | 유덕균 |
| [BOJ] 2502. 떡 먹는 호랑이 | S1 | 김도언 |
| [SWEA] 2112. 보호 필름 | D5 | 이강윤 |
| [BOJ] 20058. 마법사 상어와 파이어스톰 | G3 | 양희제, 김태학 |
| 문제 이름 | 난이도 | 발표자 및 풀이 |
|---|---|---|
| [BOJ] 1389. 케빈 베이컨의 6단계 법칙 | S1 | 박진성 |
| [SWEA] 2806. N-Queen | D3 | 양희제 |
| [SWEA] 2477. 차량 정비소 | D5 | 김태학 |
| [BOJ] 20057. 마법사 상어와 토네이도 | G3 | 이강윤 |
✅ 선택 과제
-
SQLD 시험 관련하여 공부한 흔적(개념 정리, 문제 풀이 등) - 사진도 가능!
-
다음 2문제를 해결하여 풀이 제출(17086.py, 10158.py 생성 후 풀이 제출!)
- 문제1 : [BOJ] 17086. 아기 상어 2 (실버 2)
링크 : https://www.acmicpc.net/problem/17086 - 문제2 : [BOJ] 10158. 개미 (실버 4)
링크 : https://www.acmicpc.net/problem/10158
- 문제1 : [BOJ] 17086. 아기 상어 2 (실버 2)
| 이름 | 제출 확인 |
|---|---|
| 김도언 | ✅ |
| 김태학 | ✅ |
| 박진성 | ✅ |
| 양희제 | ✅ |
| 유덕균 | ✅ |
| 이강윤 | ✅ |
| 이기용 | ✅ |
| 조용현 | ✅ |
| 문제 이름 | 난이도 | 발표자 및 풀이 |
|---|---|---|
| [BOJ] 14501. 퇴사 | S3 | 이기용, 박진성, 이강윤, 김도언 |
| [BOJ] 15686. 치킨 배달 | G5 | 조용현, 유덕균 |
| [Programmers] 92342. 양궁대회 | LV2 | 김태학, 양희제 |
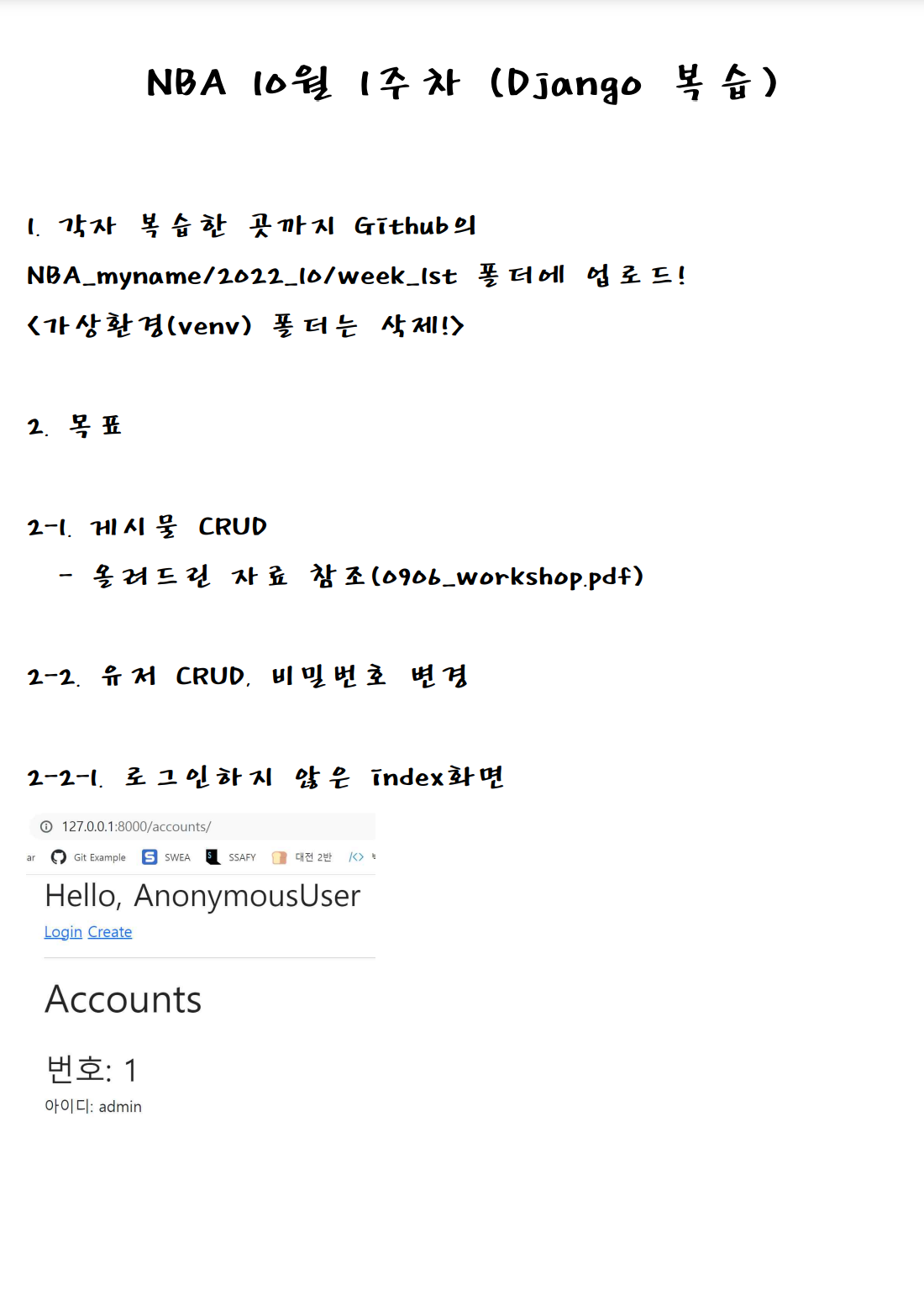
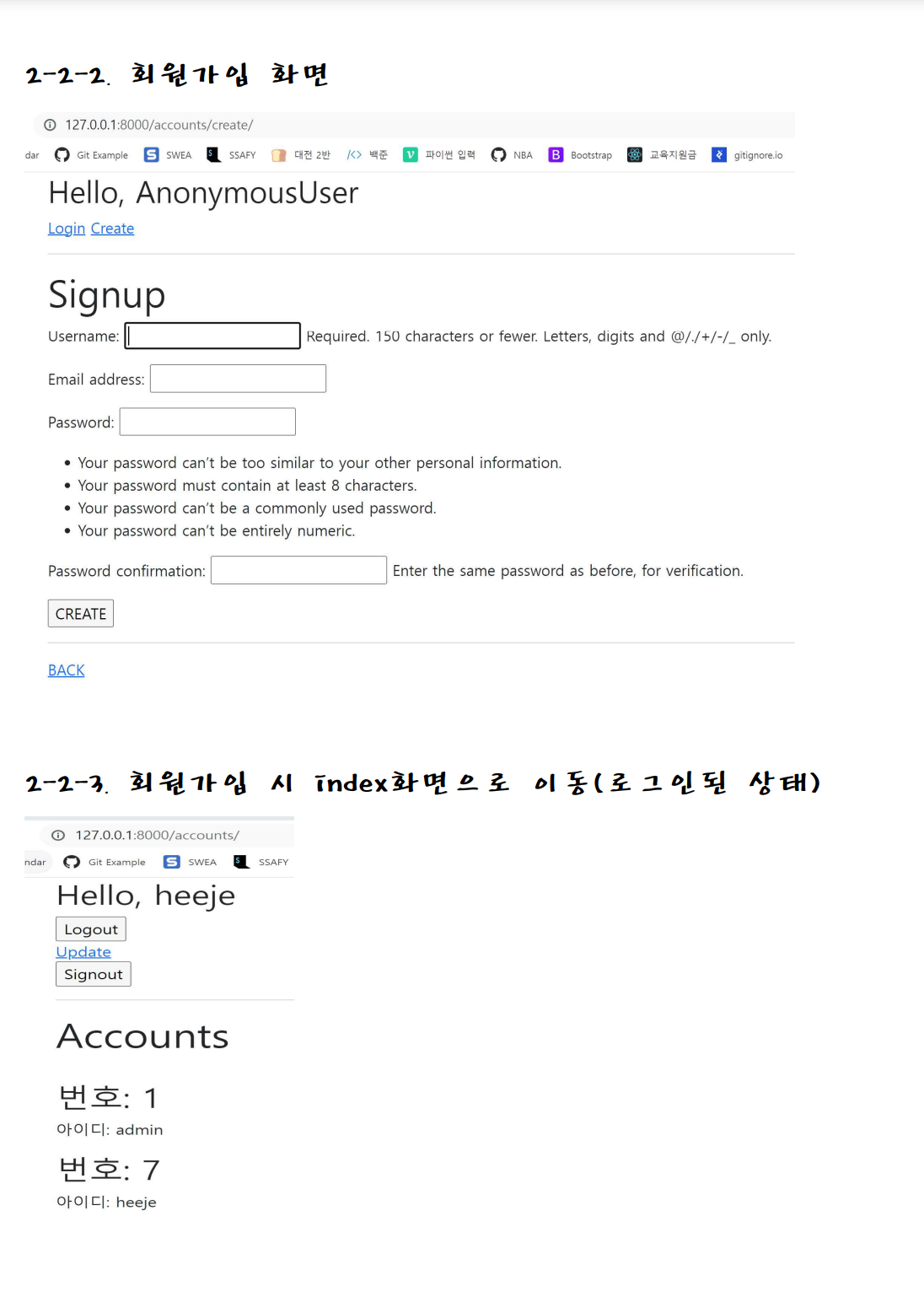
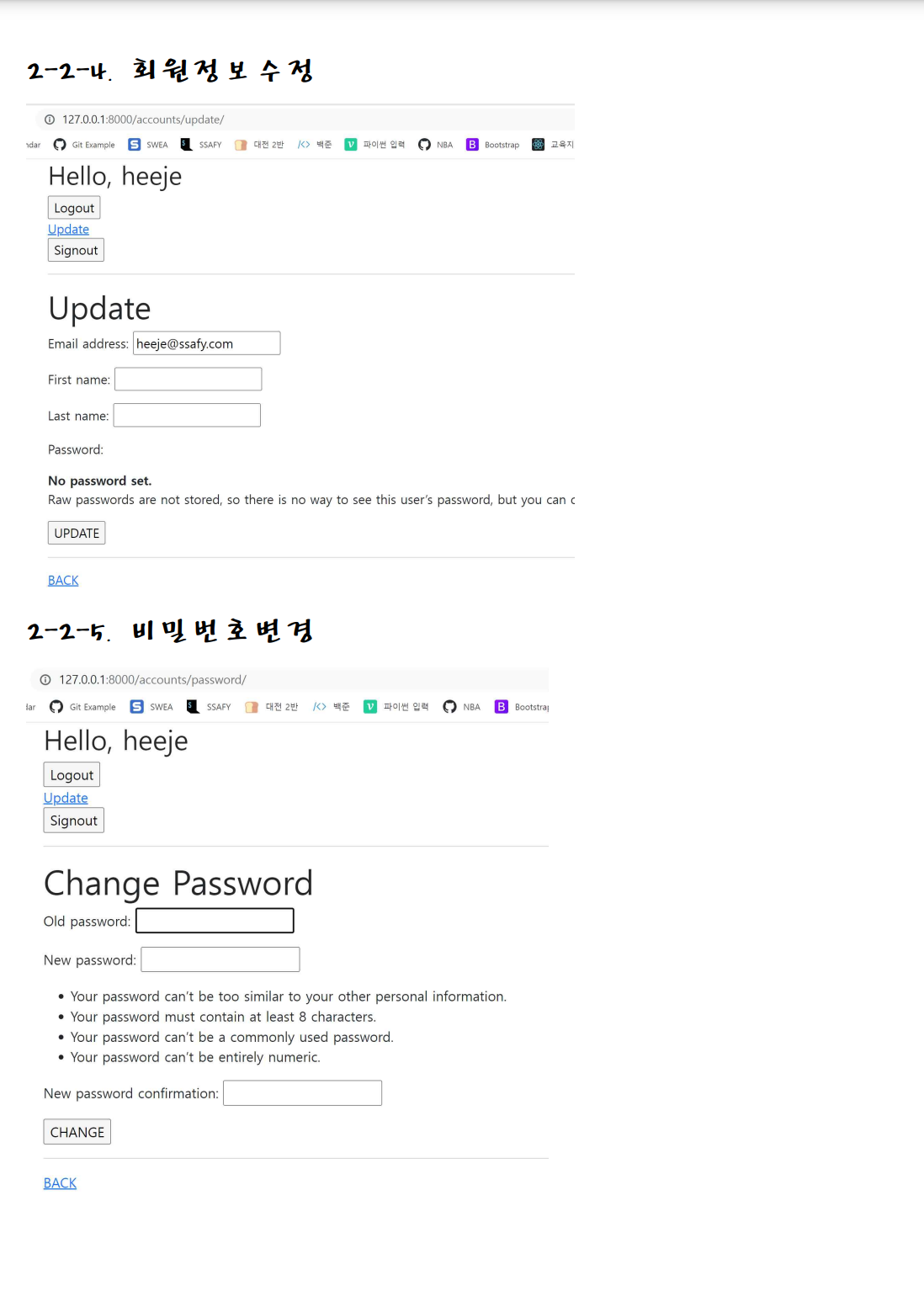
✅ Django 복습
| 이름 | 제출 확인 |
|---|---|
| 김도언 | ✅ |
| 김태학 | ✅ |
| 박진성 | ✅ |
| 송대현 | ✅ |
| 양희제 | ✅ |
| 유덕균 | ✅ |
| 이강윤 | ✅ |
| 이기용 | ✅ |
| 조용현 | ✅ |
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [SWEA] 1949. 등산로 조성 | D5 | 이강윤, 김태학 | 유덕균, 조용현 |
| [BOJ] 7576. 토마토 | G5 | 양희제, 박윤지(Guest) | 김도언, 김경아(Guest) |
| [Programmers] 64061. 크레인 인형뽑기 게임 | LV2 | 박진성, 이기용 | 양희제 |
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [BOJ] 15683. 감시 | G4 | 이강윤, 양희제 | 김도언, 조용현 |
| [Programmers] 87694. 아이템 줍기 | LV3 | 김태학, 박승재(Guest) | 양희제 |
| [Programmers] 67256. 키패드 누르기 | LV1 | 이기용, 박진성 | 유덕균, 장현혁(Guest) |
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [SWEA] 14510. 나무 높이 | D3 | 김태학, 양희제 | 조용현, 전동준(Guest) |
| [BOJ] 16236. 아기 상어 | G3 | 이강윤, 허정범(Guest) | 김도언, 유덕균 |
| [Programmers] 68645. 삼각 달팽이 | LV2 | 이기용, 박진성 | 양희제 |
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [SWEA] 1952. 수영장 | D4 | 김태학, 이강윤 | 양희제, 오태훈(Guest) |
| [BOJ] 2635. 수 이어가기 | S5 | 이기용, 이가은(Guest) | 김도언, 조용현 |
| [Programmers] 42888. 오픈채팅방 | LV2 | 양희제, 박진성 | 송대현, 유덕균 |
9월 1주차 회의 내용 관련 개념 정리
필요한 계산 값을 저장해두었다가 재사용하는 알고리즘 설계 기법
다이나믹 프로그래밍은 다음과 같은 조건을 만족할 때 사용할 수 있습니다.
- 최적 부분 구조
- 큰 문제를 작은 문제로 나눌 수 있고, 이러한 작은 문제의 답을 모아 큰 문제를 해결할 수 있습니다.
- 중복된 하위 문제
- 동일한 작은 문제를 반복적으로 해결해야 합니다.
피보나치 수열
- 다이나믹 프로그래밍으로 해결할 수 있는 대표적인 예시가 바로 피보나치 수열입니다. 피보나치 수열은 현재 항을 계산하기 위해 이전 두 항의 합을 구해야 합니다. 이를 재귀함수를 사용하여 코드로 구현하게 되면 다음과 같습니다.
def fibo(x):
if x==1 or x==2:
return 1
return fibo(x-1) + fibo(x-2)
print(fibo(5))-
해당 코드는 O(2^N)의 시간복잡도를 가지게 되어 N이 증가함에 따라 수행시간이 기하급수적으로 늘어나게 됩니다. 예를 들어 N=30이면 약 10억 가량의 연산을 수행해야 합니다.
Topdown -
탑다운 방식은 메모이제이션을 사용하여 다이나믹 프로그래밍을 구현하는 방식 중 하나입니다. 메모이제이션(memoization)이란 한번 구한 계산 결과를 메모리 공간에 메모해두고, 같은 식을 다시 호출하면 메모한 결과 그대로 가져오는 기법을 말합니다. 탑다운 방식은 큰 문제를 해결하기 위해 작은 문제를 호출한다고 하여 하향식이라고도 불리는데, 이러한 탑다운방식은 재귀함수를 이용하여 구현할 수 있습니다.
# 한번 계산된 결과를 메모이제이션하기 위한 리스트
memo = [0]*100
# 피보나치 수열을 재귀함수로 구현(topdown)
def fibo(x):
# fibo(1)=fibo(2)=0
if x==1 or x==2:
return 1
# 이미 계산한 적 있는 문제라면 그대로 반환
if memo[x] != 0:
return memo[x]
# 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
memo[x] = fibo(x-1)+fibo(x-2)
return memo[x]
print(fibo(99))
Bottom-Up
-
바텀-업 방식은 타블레이션(tabulation)을 사용하여 다이나믹 프로그래밍을 구현하는 방식 중 하나입니다. 타블레이션(tabulation)이란 하위 문제부터 천천히 해결하면서 더 큰 문제를 해결하는 기법을 말하는데, 이렇게 부르는 이유는 작은 문제부터 큰 문제까지 하나하나 테이블을 채워간다는 의미 때문입니다. 바텀-업 방식은 하위 문제부터 시작해서 더 큰 문제를 해결해 나가기 때문에 상향식이라고도 부릅니다. 다이나믹 프로그래밍의 전형적인 형태는 바로 이 바텀업 방식인데, 이는 반복문을 이용하여 구현할 수 있습니다.
-
구현 방법
# 작은 문제부터 해결해서 저장할 dp테이블 dp = [0]*100 # fibo(1)=fibo(2)=0 dp[1]=1 dp[2]=1 n=99 # 피보나치 수열을 반복문으로 구현(bottom up) for i in range(3, n+1): dp[i] = dp[i-1]+dp[i-2] print(dp[n])
출처 : DOing
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [SWEA] 4013. 특이한 자석 | D4 | 양희제, 이용준(Guest) | 유덕균, 송대현 |
| [SWEA] 1220. Magnetic | D3 | 박진성, 이기용 | 김도언, 김도희(Guest) |
| [Programmers] 60058. 괄호 변환 | LV2 | 김태학, 이강윤 | 양희제, 조용현 |
9월 2주차 회의 내용 관련 개념 정리
deque란, 쉽게 말해서 파이썬의 list와 같이 요소들을 한 곳에 담아두는 배열입니다. 파이썬에서 queue는 선입선출(FIFO)의 방식으로 작동되는데, deque는 양쪽 방향 모두에서 요소를 추가 및 제거할 수 있다는 점에서 양방향인 queue라고 할 수 있겠습니다.
List도 있는데 굳이 deque를 사용하는 이유는?
-
List보다 Deque의 속도가 훨씬 빠르기 때문입니다. list는 O(n)의 속도, deque는 O(1)의 속도를 갖습니다. 리스트와 같은데 굳이 import를 해가면서 쓰는 이유는 위와 같이 속도, 성능 면에서의 장점 때문이라고 할 수 있습니다.
-
사용 방법
from collections import deque
q = deque()
q1 = deque(maxlen=9) # 최대 길이가 9인 deque 생성-
사용가능한 메서드들
q.append(item): 오른쪽 끝에 삽입q.appendleft(item): 왼쪽 끝에 삽입q.pop(): 가장 오른쪽의 요소 반환 및 삭제q.popleft(): 가장 왼쪽의 요소 반환 및 삭제q.extend(array): 주어진 array 배열을 순환하며 q의 오른쪽에 추가q.extendleft(array): 주어진 array 배열을 순환하며 q의 왼쪽에 추가q.remove(item): 해당 item을 q에서 찾아 삭제q.rotate(숫자): 해당 숫자만큼 회전 (양수 : 시계방향, 음수 : 반시계 방향)
Stack -
스택의 특성
- 물건을 쌓아 올리듯 자료를 쌓아 올린 형태의 자료구조입니다.
- 스택에 저장된 자료는 선형 구조를 갖습니다.
- 선형구조 : 자료 간의 관계가 1대1의 관계를 갖습니다.
- 비선형구조 : 자료 간의 관계가 1대N의 관계를 갖습니다.
- 스택에 자료를 삽입하거나 스택에서 자료를 꺼낼 수 있습니다.
- 마지막에 삽입한 자료를 먼저 꺼내는 후입선출(LIFO, Last-In-First-Out)의 구조를 갖습니다.
-
사용법
stack.append(요소): 괄호 안의 요소를 리스트 맨 뒤에 삽입stack.pop(): 리스트의 맨 뒤 요소를 삭제
출처 : Block Chain & NFT
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [SWEA] 4008. 숫자 만들기 | D4 | 김태학, 임성빈(Guest) | 양희제, 김진호(Guest) |
| [SWEA] 1211. Ladder2 | D4 | 양희제, 이강윤 | 김도언, 조용현 |
| [Programmers] 17681. [1차] 비밀지도 | LV1 | 박진성, 이기용 | 유덕균, 송대현 |
| 문제 이름 | 난이도 | 발표자 및 풀이(1팀) | 발표자 및 풀이(2팀) |
|---|---|---|---|
| [SWEA] 1244. 최대 상금 | D3 | - | 김도언 |
| [Programmers] Test. 이진 트리 | LV3 | 김태학 | - |
| [SWEA] 5207. 이진 탐색 | D3 | 박진성 | - |
| [SWEA] 5024. 병합 정렬 | D3 | 양희제 | 송대현 |
| [SWEA] 5650. 핀볼 게임 | D4 | - | 유덕균 |
| [Programmers] Test. 이모티콘 | LV3 | 이강윤 | - |
| [SWEA] 5178. 노드의 합 | D3 | 이기용 | - |
| [BOJ] 1991. 트리 순회 | S1 | - | 조용현 |
![[Programmers] Test. 이진 트리](https://github.com/HeeJeYang/Navigate-Basic-Algorithms/blob/master/NBA_taehak/2022_09/week_4th/bin_tree.png){kind=link}
| 문제 번호 | 문제 이름 | 난이도 | 발표자(1팀) | 풀이(1팀) | 발표자(2팀) | 풀이(2팀) |
|---|---|---|---|---|---|---|
| 1545 | 거꾸로 출력해 보아요 | D1 | 김태학 | 바로 가기 | 유덕균 | 바로 가기 |
| 2019 | 더블더블 | D1 | 이강윤 | 바로 가기 | 조용현 | 바로 가기 |
| 1936 | 1대1 가위바위보 | D1 | 이기용 | 바로 가기 | 김도언 | 바로 가기 |
| 1959 | 두 개의 숫자열 | D2 | 양희제 | 바로 가기 | 송대현 | 바로 가기 |
| 1204 | 최빈수 구하기 | D2 | 박진성 | 바로 가기 | 양희제 | 바로 가기 |
8월 1주차 회의 내용 관련 개념 정리
packing은 여러 개의 객체를 하나로 합쳐줄 때 사용하는 반면, 이와 반대되는 개념인 unpacking은 여러 개의 객체를 포함하고 있는 하나의 객체를 풀어줍니다.
# 예시
numbers = [1, 2, 3]
print(*numbers) # 1 2 3
# 언패킹 되는 과정
# 1. print(*numbers)
# 2. print(*[1, 2, 3])
# 3. print(1, 2, 3)
# 4. 1 2 3이 출력됨
range 함수는, 연속적인 숫자 객체를 만들어서 반환해주는 함수입니다. 불변형이고, 순서가 있는 시퀀스형입니다. 반복문 for와 함께 사용이 되기 때문에 알아둬야 할 필수 요소라고 생각하시면 되겠습니다.
# 예시
for a in range(4):
print(a, end=' ') # 0 1 2 3 (4는 출력되지 않습니다.)
for b in range(1, 5):
print(b, end=' ') # 1 2 3 4 (5는 출력되지 않습니다.)
for c in range(1, 6, 2):
print(c, end=' ') # 1 3 5
for d in range(5, 2, -1):
print(d, end=' ') # 5 4 3 (2는 출력되지 않습니다.)
프로그래밍 언어, 특히 c언어로 swap을 시도하면 이렇습니다.
a = 30
b = 50
temp = a
a = b
b = temp
print(a, b) # 50 30
하지만 파이썬에게는 파이써닉(pythonic)한 코드가 있습니다.
a = 30
b = 50
a, b = b, a
print(a, b) # 50 30
물론 파이써닉한 코드도 좋은 코드이지만 회의에서도 말씀드렸다시피 가독성이 좋은 코드가 더 좋은 코드라고 할 수 있겠습니다!! 🙂
파이썬에서 문자열을 표현하는 방법은 여러 가지가 있지만, 그 중 가장 최근에 나왔으면서 깔끔한 표현방법이 f-string입니다. 다들 잘 사용하고 계셔서 다행입니다!
team_name = "NBA"
count_members = 9
print(f'저희 그룹스터디 이름은 {team_name}이며, 팀원은 총 {count_members}명입니다.')
# 저희 그룹스터디 이름은 NBA이며, 팀원은 총 9명입니다.| 문제 번호 | 문제 이름 | 난이도 | 발표자(1팀) | 풀이(1팀) | 발표자(2팀) | 풀이(2팀) |
|---|---|---|---|---|---|---|
| 1933 | 간단한 N 의 약수 | D1 | 양희제 | 바로 가기 | 양희제 | 바로 가기 |
| 1938 | 아주 간단한 계산기 | D1 | 이강윤 | 바로 가기 | 송대현 | 바로 가기 |
| 1284 | 수도 요금 경쟁 | D2 | 김태학 | 바로 가기 | 유덕균 | 바로 가기 |
| 1288 | 새로운 불면증 치료법 | D2 | 이기용 | 바로 가기 | 조용현 | 바로 가기 |
| 1940 | 가랏! RC카! | D2 | 박진성 | 바로 가기 | 김도언 | 바로 가기 |
8월 2주차 회의 내용 관련 개념 정리
표현식과 제어문을 통해 특정한 값을 가진 리스트를 간결하게 생성하는 방법
- List Comprehension의 과정
a = []
# List Comprehension의 과정을 제어문으로 만들어 보면..
for i in range(5):
if i % 2 == 1:
a.append(i)
# 마법의 복사 붙여넣기
# for문 그대로 들고가서 가운데, if문을 그 오른쪽에, 출력할 값을 왼쪽에!
a = [i for i in range(5) if i % 2 == 1]-
알고리즘 문제 풀 때 많이 활용됨!!
[code for 변수 in iterable] [code for 변수 in iterable if 조건식] # [1, 2, 3, 4, ...] 에서 [2, 4, 6, 8...] 뽑아낼 떄 등 많이 사용됨!
Set이란, 중복되는 요소가 없이, 순서에 상관없는 데이터들의 묶음입니다. 담고 있는 요소를 삽입 변경, 삭제 가능한 가변 자료형입니다. 셋을 활용하면 다른 컨테이너에서 중복된 값을 쉽게 제거할 수 있습니다. 하지만 순서가 무시되기 때문에 순서가 중요한 경우 사용할 수 없습니다.
# Set은 중복 값 제거
print({1, 2, 3, 1, 2}) # {1, 2, 3}
print(type({1, 2, 3})) # <class 'set'>
# 빈 중괄호는 Dictionary
blank = {}
print(type(blank)) # <class 'dict'>
blank_set = set()
print(type(blank_set)) # <class 'set'>
# Set은 순서가 없어 인덱스 접근 등 특정 값에 접근할 수 없음
print({1, 2, 3}[0]) # TypeError: 'set' object is not subscriptable-
다양한 셋 메서드
-
s.copy() : 셋의 얕은 복사본을 반환
-
s.add(x) : 항목 x가 셋 s에 없다면 추가
-
s.pop() : 셋 s에서 랜덤하게 항목을 반환하고, 해당 항목을 제거. set이 비어있을 경우 KeyError
-
s.remove(x) : 항목 x를 셋 s에서 삭제. 항목이 존재하지 않을 경우 KeyError
-
s.discard(x) : 항목 x가 셋 s에 있는 경우, 항목 삭제
-
s.update(t) : 셋 t에 있는 모든 항목 중 셋 s에 없는 항목을 추가
-
s.clear() : 모든 항목을 제거
-
s.isdisjoint(t) : 셋 s가 셋 t와 서로 같은 항목을 하나라도 갖고 있지 않은 경우, True 반환(서로소)
-
s.issubset(t) : 셋 s가 셋 t의 하위 셋인 경우, True 반환
-
s.issuperset(t) : 셋 s가 셋 t의 상위 셋인 경우, True 반환
자연수 n의 약수를 구할 때 좀 더 효율적인 방법이 있습니다. 바로 n의 제곱근이하의 자연수들만 반복문으로 돌리는 것입니다.
왜냐하면, '임의의 자연수 N의 약수들 중에서 두 약수의 곱이 N이 되는 약수 A와 약수 B는 반드시 존재한다'는 규칙이 존재하기 때문에, 자연수 N의 제곱근까지의 약수를 구하면 그 짝이 되는 약수는 자동으로 구해지기 때문입니다.
# 단순 풀이 (시간복잡도 O(N)) def get_divisor(n): n = int(n) divisors = [] for i in range(1, n + 1): if (n % i == 0): divisors.append(i) return divisors # 효율화 풀이 (시간복잡도 O(N^(1/2))) def get_divisor(n): n = int(n) divisors = [] divisors_back = [] for i in range(1, int(n**(1/2)) + 1): if (n % i == 0): divisors.append(i) if (i != (n // i)): divisors_back.append(n//i) return divisors + divisors_back[::-1]
출처 : GangYunGit_TIL, 이누의 개발성장기
-
| 문제 번호 | 문제 이름 | 난이도 | 발표자(1팀) | 풀이(1팀) | 발표자(2팀) | 풀이(2팀) |
|---|---|---|---|---|---|---|
| 2025 | N줄덧셈 | D1 | 이강윤 | 바로 가기 | 양희제 | 바로 가기 |
| 2027 | 대각선 출력하기 | D1 | 김태학 | 바로 가기 | 김도언 | 바로 가기 |
| 1945 | 간단한 소인수분해 | D2 | 박진성 | 바로 가기 | 유덕균 | 바로 가기 |
| 1946 | 간단한 압축풀기 | D2 | 양희제 | 바로 가기 | 조용현 | 바로 가기 |
| 1948 | 날짜 계산기 | D2 | 이기용 | 바로 가기 | 송대현 | 바로 가기 |
8월 3주차 회의 내용 관련 개념 정리
알고리즘의 로직을 코드로 구현할 때, 시간 복잡도를 고려한다는 것은 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가? 와 같습니다. 즉 효율적인 알고리즘을 구현한다는 것은 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘이라고 말할 수 있습니다.
시간 복잡도를 표기하는 방법
-
최악의 경우 : Big-O(빅-오) ⇒ 상한 점근
-
최선의 경우 : Big-Ω(빅-오메가) ⇒ 하한 점근
-
중간의 경우 : Big-θ(빅-세타) ⇒ 그 둘의 평균
Big-O 표기법은 최악의 경우를 고려하므로, 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있다.
- N줄덧셈
# N줄덧셈
T = int(input())
print(T * (T + 1) // 2)
# 1. 등차수열의 합 공식
# 시간복잡도 : O(4) = O(1)
# sum = N * (N + 1) // 2
# 2. 1부터 N까지 반복문을 돌며 합을 계산
# 시간복잡도 : O(N)
# sum = 0
# for i in range(1, N + 1):
# sum += i-
1초가 걸릴 때 입력의 최대 크기
- O(N) : 약 1억
- O(N^2) : 약 1만
- O(N^3) : 약 500
- O(2^N) : 약 20
- O(N!) : 10
zip() 함수는 여러 개의 iterable한 객체를 인자로 받고 각 객체가 담고 있는 원소를 튜플의 형태로 차례로 접근할 수 있는 반복자(iterator)를 반환합니다.
open_brackets = ['(', '[', '{', '<']
closed_brackets = [')', ']', '}', '>']
for pair in zip(open_brackets, closed_brackets):
print(pair)
# ('(', ')')
# ('[', ']')
# ('{', '}')
# ('<', '>')위 코드와 같이, zip() 함수를 사용하면 마치 옷의 지퍼를 올리는 것처럼 양 측에 있는 데이터를 하나씩 차례로 짝을 지어줍니다.
- 활용 예시
# 2차원 리스트 다루기
a = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
# 90도 회전
rotated_a = list(zip(*a[::-1]))
# [
# [7, 4, 1],
# [8, 5, 2],
# [9, 6, 3]
# ]
# 행과 열 바꾸기
change_row_and_col_a = list(zip(*a))
# [
# [1, 4, 7],
# [2, 5, 8],
# [3, 6, 9]
# ]출처 : ONOFF.log
| 문제 번호 | 문제 이름 | 난이도 | 발표자(1팀) | 풀이(1팀) | 발표자(2팀) | 풀이(2팀) |
|---|---|---|---|---|---|---|
| 2029 | 몫과 나머지 출력하기 | D1 | 박진성 | 바로 가기 | 조용현 | 바로 가기 |
| 2043 | 서랍의 비밀번호 | D1 | 이기용 | 바로 가기 | 김도언 | 바로 가기 |
| 1961 | 숫자 배열 회전 | D2 | 김태학 | 바로 가기 | 송대현 | 바로 가기 |
| 1966 | 숫자를 정렬하자 | D2 | 양희제 | 바로 가기 | 양희제 | 바로 가기 |
| 1970 | 쉬운 거스름돈 | D2 | 이강윤 | 바로 가기 | 유덕균 | 바로 가기 |
| 2563 | BOJ - 색종이 | B1 | 김영주 교수님 | Guest 풀이 | 김영주 교수님 | Guest 풀이 |
8월 4주차 회의 내용 관련 개념 정리
정렬이란, 2개 이상의 자료를 특정 기준에 의해 작은 값부터 큰 값(오름차순), 혹은 그 반대의 순서대로(내림차순) 재배열하는 것을 의미합니다.
대표적인 정렬 방식의 종류
- 버블 정렬(Bubble Sort)
- 카운팅 정렬(Counting Sort)
- 선택 정렬(Selection Sort)
- 퀵 정렬(Quick Sort)
- 삽입 정렬(Insertion Sort)
- 병합 정렬(Merge Sort)
이번 회의에서는 이전에 학습하였던 버블 정렬과 카운팅 정렬, 그리고 내장 함수인 sort에 대해 알아보았습니다.
버블 정렬
- 인접한 두 개의 원소를 비교하며 자리를 계속 교환하는 방식입니다.
- 정렬 과정
- 첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 마지막 자리까지 이동합니다.
- 한 단계가 끝나면 가장 큰 원소가 마지막 자리로 정렬됩니다.
- 교환하며 자리를 이동하는 모습이 물 위에 올라오는 거품 모양과 같다고 하여 버블 정렬이라고 합니다.
- 시간 복잡도(O(n^2))
- 구현 방법
T = int(input())
for tc in range(1, T + 1):
N = int(input())
numbers = list(map(int, input().split()))
for j in range(N - 1, 0, -1):
for i in range(j):
if numbers[i] > numbers[i + 1]:
numbers[i], numbers[i + 1] = numbers[i + 1], numbers[i]
print(f"#{tc}", *numbers)
카운팅 정렬(Counting Sort)
-
항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
-
제한 사항
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능 : 각 항목의 발생 횟수를 기록하기 위해, 정수 항목으로 인덱스되는 카운트들의 배열을 사용하기 때문입니다.
- 카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 합니다.
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능 : 각 항목의 발생 횟수를 기록하기 위해, 정수 항목으로 인덱스되는 카운트들의 배열을 사용하기 때문입니다.
-
시간 복잡도(O(n + k))
-
구현 방법
T = int(input()) for tc in range(1, T + 1): N = int(input()) numbers = list(map(int, input().split())) max_num = max(numbers) c = [0] * (max_num + 1) sorted_numbers = [] for number in numbers: c[number] += 1 for i in range(len(c)): while c[i]: sorted_numbers.append(i) c[i] -= 1 print(f"#{tc}", *sorted_numbers)
sort(), sorted() -
sort, sorted는 내장함수이며, 내부적으로 병합 정렬을 적용하고 있습니다. 병합 정렬을 이용할 시 최악의 경우에도 O(NlogN)의 시간복잡도를 보장해준다는 장점이 있습니다.
배열 회전에 관한 zip 활용 예시
# 2차원 리스트 다루기
a = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
# 90도 회전
rotated_a = list(zip(*a[::-1]))
# [
# [7, 4, 1],
# [8, 5, 2],
# [9, 6, 3]
# ]
# 행과 열 바꾸기
change_row_and_col_a = list(zip(*a))
# [
# [1, 4, 7],
# [2, 5, 8],
# [3, 6, 9]
# ]