Finite difference discretization order for UpwindDifference

[archermarx]

Hi all, I'm loving the DiffEq ecosystem a lot and I wanted to thank yall for implementing Neumann and Robin BCs this week. I was running some tests on basic linear advection and was testing out higher order finite differences and found that specifying an order above 1 when applying the MOLFiniteDifference function made no difference to the approximation.

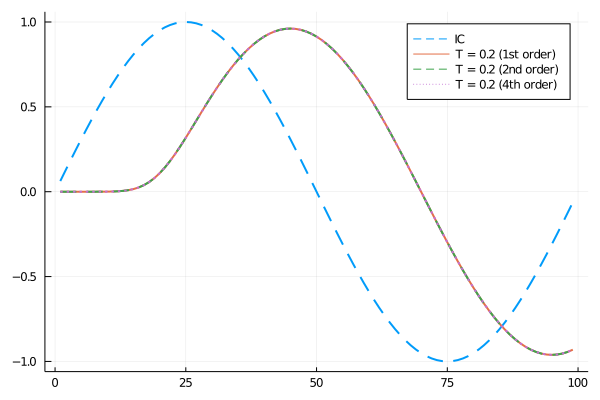
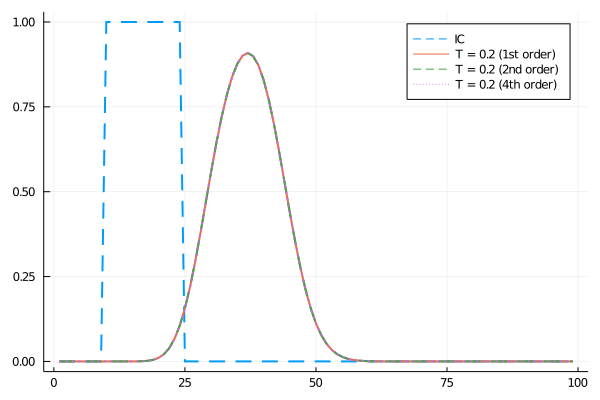
Investigating the code, I found this in the discretize_2 function:

 if deriv_order == 0
      expr = :(u[:,$j])
  elseif deriv_order == 1
      # TODO: approx_order and forward/backward should be

      #       input parameters of each derivative
      approx_order = 1
      L = UpwindDifference(deriv_order,approx_order,dx[i],len_of_indep_vars[i]-2,-1)
      expr = :(-1*($L*Q[$j]*u[:,$j]))
  elseif deriv_order == 2
      L = CenteredDifference(deriv_order,approx_order,dx[i],len_of_indep_vars[i]-2)
      expr = :($L*Q[$j]*u[:,$j])
  end

If I understand this correctly, first derivatives are always discretized using a first order upwind finite difference, which would explain what I saw. Is there a reason that the UpwindDifference doesn't support higher derivatives at this time?

[ChrisRackauckas]

That's a mistake. It should allow for higher order upwinding. We need to allow for specifying the order of centered and upwinding operators separately in the MOLFiniteDifference constructor though.

[archermarx]

Ok! good to know. I can try and put together a PR then.