במפקדי האוכלוסין שנערכו מדי עשור בארצות הברית מאז לידתה, שיטת הרישום היתה פשוטה. נציגים היו לוקחים מכל אזרח את פרטיו, רושמים את הפרטים על פתק נייר, ושולחים את כל הפתקים למטה המרכזי של המפקד.
באמצע המאה התשע עשרה (1850) האוכלוסייה כמובן גדלה, והספירה הידנית של כל הפתקים נהיית מייגעת ומועדת לטעויות. להוסיף על הכאוס הקיים, הייתה גם דרישה חדשה בקונגרס, לאסוף פרטים נוספים במפקד האוכלוסין, כמו מין, צבע עור, מצב כלכלי ועוד נתונים. וכך, תהליך הספירה באמצעות פתקים הפך להיות כמעט בלתי אפשרי. מנגד, טעות הייתה בלתי אפשרית, שכן הייצוג בקונגרס מבוסס על מפקד האוכלוסין, ולספירה או טעויות בספירה היו משמעויות פוליטיות טעונות.
בשנת 1890+- ממשלת ארה"ב הכריזה על תחרות ליצור תהליך שייעל את הספירה ההצעה שזכתה הייתה של הרמן הולרית' (Herman Hollerith) שהציג מכונה המבוססת על כרטיסי ניקוב בשם "מכונת טבולציה" (Tabulating machine) את הרעיון הוא קיבל מכך שראה בכרטיסי רכבת היה סימון של צבע שיער והמבקר היה מנקב את הכרטיס לפי צבע השיער של הנוסע כדי למנוע העברה של הכרטיס מאדם לאדם.
בשביל מפקד האוכלוסין השתמשו בכרטיס הזה (ליתר דיוק הכרטיס היה ריק. התמונה היא רק מפה איפה לנקב.)
הסוקר ניקב את הכרטיס לפי פרטי האזרח. למשל, הסימון של גבר בן 50 היא ניקוב של האות M ושל המספר 50.
העובד במרכז המיון הכניס את הכרטיס למכונה (בצד שמאל בתמונה הבאה) עם כוסיות עופרת שעמדו מתחת לכל הנקודות בכרטיס ואז הניח מעליו לוח עם מחטים והפעיל את המכונה במקום שהיה חור המחט נגעה בתושבת שמתחת לכרטיס וסגרה מעגל. על כל סגירת מעגל המונה של הנקודה הזאת עלה באחד. כך בתוך זמן קצר אפשר למנות את כל האוכלוסיה של המדינה עם פירוט כמה מתוכם הם גברים/נשים וכו'. בהמשך הוסיפו מכונת מיון (המכשיר מצד ימין בתמונה הבאה) הכללים היו מובנים מראש ואם המעגל נסגר בנקודה X התא המיועד נפתח והעובד הכניס את הכרטיס לתוכו. בהמשך הוסיפו מנגנון שמכניס את כל הכרטיסים באופן אוטומטי בלי צורך שעובד יכניס את הכרטיסים באופן ידני.
אחרי ההצלחה עם ממשלת ארה"ב Herman הקים חברה מסחית שלימים הפכה להיות IBM. לשכות האוכלוסין ממדינות נוספות בעולם עבדו עמו. והשכיר את המכונות האלו לממשלות שונות וגם לחברות מסחריות.
בהמשך נוספו עוד יכולות כמו מכונה שמנקבת כרטיסים אחרים ועם לוח בקרה יכלו "לתכנת" את המכונה שתעשה פעולות שונות כשיש מתח בנקודה מסויימת
הנה תיאור איך מבצעים כפל עם הלוח הזה:
If I wanted to multiply, say, 12 times 15, I would punch a one and a two into the first column of a card and the second column of a card, then in the third column I would put another one and in the fourth column I would put a five. So the first two spots would be one and two and that would go into place on the plug board that shows it is the multiplier, and then the third and fourth spots on the card would go to a place that showed it was the multiplicand. And then there was a third slot that was to be the result, and that would punch the answer into whichever column on the card you wanted to put it in. And then you would need six wires to complete that.
בשלב מסויים, בגלל שלכל חברה היה צרכים שונים, יצרו לוח גנרי בצורה שאפשרה "לכתוב" על הכרטיס מידע דינמי. בכל כרטיס היה 80 עמודות ו12 שורות, בכל עמודה אפשר לכתוב תו אחד, כך שיש 80 תווים בכרטיס. שורות 0-9 חור בכל אחד מהם מסמן את הספרה המתאימה, שורה 11 נקראת X שורה 12 נקראת Y אם רק Y מנוקב זה מסמן את התו & ואם רק X מנוקב זה מסמן את התו -. הABC חולק ל3 קבוצות וסומן עם 2 ניקובים. למשל 12+1=A 12+2=B 11+1=J וכן הלאה. 0+9=Z השורה 0 שימשה גם כסמן וגם שסימון לספרה 0
אין ספק שיש כאן הרבה בזבוז של מקום על הדף, למה לסמן רק עם 2 ניקובים כשאפשר ליצור עוד הרבה סוגי שילובים, בשביל לייצר עוד סוגי תווים בפחות מקום?
במשך השנים עברו לשמירת המידע על חומרים אחרים, שאפשרו לשמור יותר מידע על כל ס"מ, וגם לכתוב ולמחוק ללא הגבלה. היצוג של חור מנוקב או לא, בוצע על ידי כתיבה של 0 ו 1. חור=דלוק=1 בלי חור=כבוי=0
למשל, סרט מגנטי: מגנט שפונה למעלה=1 למטה=0. או חורים בדיסק, ומחט עוברת על הדיסק ו"קוראת" איפה יש חורים. כיום שומרים את המידע בתאים קטנים, שאפשר לטעון אותם בשדה מגנטי. אבל הרעיון הבסיסי נשאר זהה:ל המידע נשמר ב0 או 1.
בשנות ה60 הגיעו לסטנדרט של שמירת מידע (צריך להרחיב יותר בסיפור הזה) וקבעו שלכל נקודת מידע קוראים ביט (bit) ולכל שמונה ביטים קוראים בייט (byte).
בשונה מהשיטה של IBM לעיל שלא מנצלת את כל הצירופים שאפשר לשמור כאן יצרו סטנדרט שבו אפשר לנצל את כל הצירופים החשבון פשוט ב8 ביט אפשר לשמור עד 256 בא נתחיל מחשבון של 2 ביט בו אפשר לשמור 4 צירופים 00=0 01=1 10=2 11= 3 עכשיו כל ביט שמוסיפים מכפיל את האפשרויות ב2 אם יש לנו 3 ביט אז יש לנו 8 צרופים כל הצירופים שהיה לנו עם 2 ביטים עם 0 בהתחלה או עם 1 בהתחלה
000=0
010=1
010=2
011=3
100=4
110=5
110=6
111=7
וכן הלאה
4=16
5=32
6=64
7=128
8=256
אז בבייט אנחנו יכולים לשמור מספר עד 255 או לשמור טקסט, איך נשמור טקסט? מסכמים על לוח האותיות וכל אות מקבלת מספר כך למשל האות A מסומנת עם המספר 65 בהמשך רצו להוסיף עוד אותיות משפות אחרות ובגלל שאין מקום בייצוג של 8 ביט שומרים את המידע בשני בייטים שזה 16 ביט שנותן 256X256 אפשרויות (למי שאין כח לחשב זה יוצא 65536 אפשרויות)
לשיטת ייצוג זו קוראים חשבון בינארי אפשר לעשות חשבון בדומה לחשבון שעושים בחשבון עשרוני (מה שאנחנו משתמשים ביום יום) למשל אם רוצים לעשות את החשבון הבא 01101101 + 0000001 אז 1+1=0 עם שארית 1 ואז 0+0+שארית 1 = 1 וכן הלאה וכך יוצאים עם התוצאה 01101110
כדי להמיר מספר בינארי לעשרוני צריך לחשב שהמספר הראשון שווה 1 השני 2 השלישי 4 הרביעי 8 וכן הלאה ולכן 01101110 שווה 2+4+8+32+64.
אחרי שהבנו איך זה מתבצע על הנייר צריך לנסות איך המחשב עושה את זה.
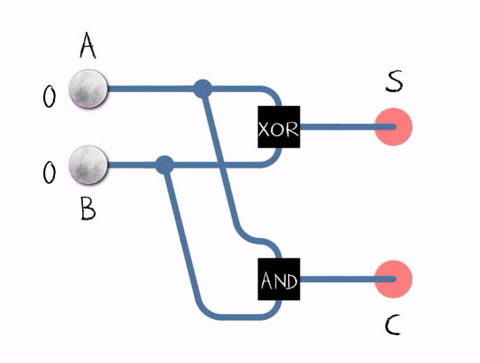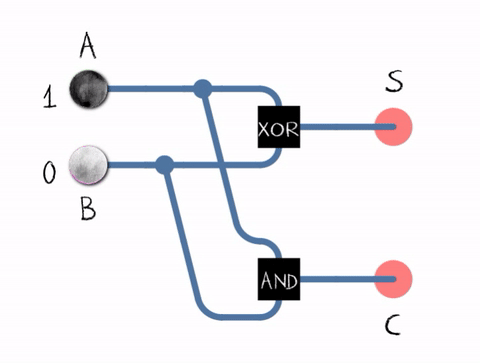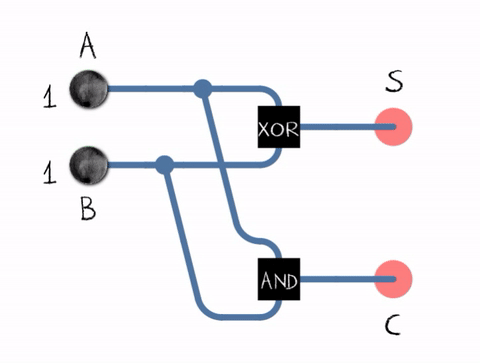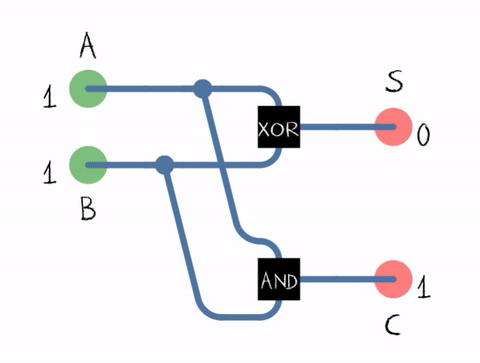
הבסיס של המעבד זה שערים לוגיים שזה רכיב שכיום עשוי לרוב מסיליקון שיש לו שתי כניסות ויציאה אחת יש כמה סוגי שערים OR זה שער שיוציא זרם אם הוא מקבל זרם באחד משני הכניסות (או בשניהם?) XOR זה שער דומה לOR אבל הוא לא יוציא זרם אם יש זרם בשני הכניסות AND זה שער שמוציא זרם רק אם הוא מקבל זרם בשני הכניסות.
בשביל לעשות חישוב חיבור פשוט (בלי שארית) אז אפשר להעביר את הביט הראשון של שני הבייטים שרוצים לחשב דרך שער OR והפלט נרשם במקום בו רוצים לשמור את הביט הראשון של התוצאה, וכן הלאה. הבעיה היא כמובן שאנחנו רוצים לשמור את השארית בשביל זה אפשר להשתמש בHalf Adder (חצי מחבר) שמורכב משני שערים השער הראשון XOR מחשב את הקלט של שני הביטים אם זה 0+1 הפלט יהיה 1 אם זה 0+0או 1+1 הפלט יהיה 0 בנוסף נעביר את הקלט של שני הביטים דרך שער AND והפלט שלו ישמר באוגר מיוחד של השארית. ורק במקרה של 1+1 הפלט שלו יהיה 1. עכשיו הבעיה היא שבביט הבא אנחנו צריכים לחשב חשבון עם 3 מקורות שני המספרים + השארית. ושבפלט יהיה בשביל זה יש מבנה קצת יותר מורכב של שערים בשם full-adder (לא יודע האם יש תועלת להכנס לכל החשבון של full-adder הרעיון הובן)
אנימציה של Half Adder מויקיפדיה
אנימציה של full-adder מויקיפדיה
אחרי שיש לנו אמצעי אחסון כל שהוא ומעבד המורכב משערים לוגיים אפשר לחשב כל חישוב כשהקלט והפלט יכול להיות אמצעי אחסון שונים.
במחשב המודרני יש אמצעי אחסון לטווח ארוך (דיסק) ואמצעי אחסון לטווח קצר. באחסון בדיסק אפשר לשמור מידע לכתיבה בלבד ע"י סימון חורים בנקודות שונות בדיסק והמחט עולה ויורדת לפי החורים, בדיסק עם אפשרות למחיקה (לא יודע איך זה עובד) אפשר לבטל את הסימונים האלו. באחסון RAM (ר"ת של ?) יש טבלה של תאים שבהם אפשר לטעון מטען מגנטי ולסמן 1 עם מטען 0 בלי מטען (תתקנו אותי אם אני טועה).
החסרון באחסון בדיסק זה המהירות קריאה\כתיבה והחסרון באחסון בRAM הוא שהמידע נמחק כשהמחשב נכבה (דהיינו שאין מתח) ובנוסף הרכיבים של RAM הרבה יותר יקרים מדיסק.