Inaccurate results using jacobian_dot(q, q_dot)

[juanjqo]

The method jacobian_dot(q, q_dot) returns inaccurate results. I performed a comparison test using a derivative Jacobian matrix analytically computed (using a two planar links robot) vs jacobian_dot. The results are not the same.
I realized that the method computes the time derivative Jacobian until joint ith. This is great, but, x_effector and J are computed until joint obj.links. Furthermore, I believe that J(:,1:i) must be computed using jacobian(theta, ith) instead of taking a column from matrix J.
I modified the method in this way:

    function J_dot = jacobian_dot(obj,theta,theta_dot, ith)
        % J_dot = jacobian_dot(theta,theta_dot) returns the Jacobian 
        % time derivative.
        % J_dot = jacobian_dot(theta,theta_dot,ith) returns the first
        % ith columns of the Jacobian time derivative.
        % This function does not take into account any base or
        % end-effector displacements.
        
        if nargin == 4
            n = ith;
        else
            n = obj.links;
        end
        
      
        %x_effector = obj.raw_fkm(theta);
        %J = obj.raw_jacobian(theta);  
        
        x_effector = obj.raw_fkm(theta, n);

        Jj = obj.jacobian(theta,n);
        Jaux = zeros(8,obj.links);
        Jaux(:,1:n) = Jj;
        J = Jaux;
        
        
        vec_x_effector_dot = J*theta_dot;
        
        x = DQ(1);            
        J_dot = zeros(8,n-obj.n_dummy);
        jth=0;
        
        for i = 0:n-1
            % Use the standard DH convention
            if strcmp(obj.convention,'standard')
                w = DQ.k;
                z = DQ(obj.get_z(x.q));
            else % Use the modified DH convention
                w = DQ([0,0,-sin(obj.alpha(i+1)),cos(obj.alpha(i+1)),0,0,-obj.a(i+1)*cos(obj.alpha(i+1)),-obj.a(i+1)*sin(obj.alpha(i+1)) ] );
                z = 0.5*x*w*x';
            end
            
            if ~obj.dummy(i+1)
                
                if jth == 0
                        Ji = zeros(8, obj.links);                           
                else
                        %ji = obj.jacobian_(theta,ith, obj.links);
                        
                        Jj = obj.jacobian(theta,jth);
                        Jaux = zeros(8,obj.links);
                        Jaux(:,1:jth) = Jj;
                        Ji = Jaux;
                end
                
                %vec_zdot = 0.5*(haminus8(w*x') + hamiplus8(x*w)*DQ.C8)*J(:,1:i)*theta_dot(1:i);
                vec_zdot = 0.5*(haminus8(w*x') + hamiplus8(x*w)*DQ.C8)*Ji*theta_dot;
                J_dot(:,jth+1) = haminus8(x_effector)*vec_zdot + hamiplus8(z)*vec_x_effector_dot;
                x = x*obj.dh2dq(theta(jth+1),i+1);
                jth = jth+1;
            else
                % Dummy joints don't contribute to the Jacobian
                x = x*obj.dh2dq(0,i+1);                    
            end
        end
    end

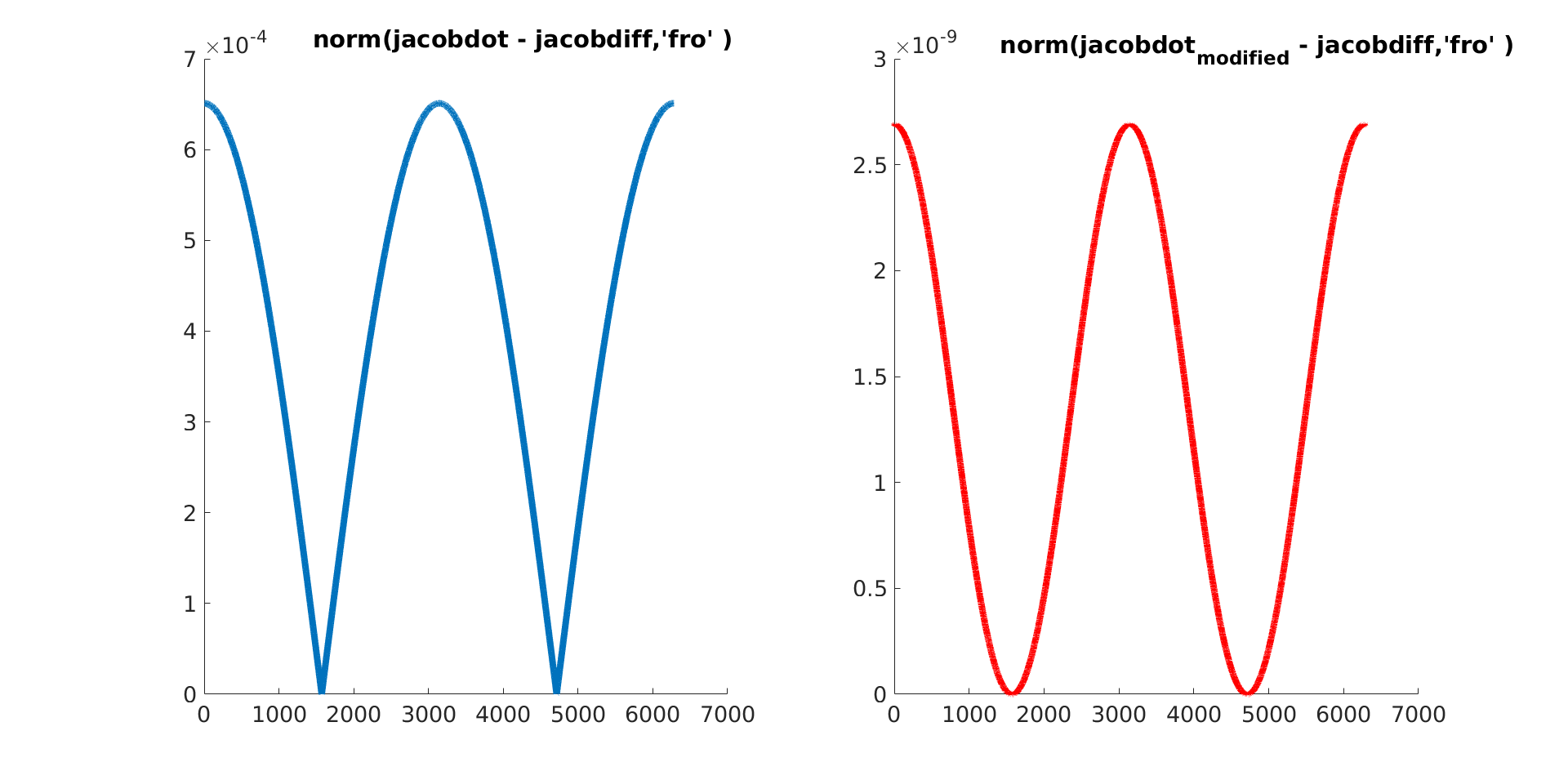
Using the modified method, the analytical derivative Jacobian matrix matched with the jacobian_dot. Furthermore, I performed the jacobian_time_derivative.m example. Using the modified method the error is lower.

[bvadorno]

Hi, Juancho. Thanks for testing the function. Indeed, this bug inherits the bug mentioned in issue #1. I've just fixed it. Please take a look at my implementation as I didn't use auxiliary matrices and I also implemented the possibility of using jacobian_dot up to the i-th link. Could you please test it again?

Cheers,
Bruno

[juanjqo]

Sure!
There is some problem with matrix dimensions.

q = randn(n,1);
q_dot = randn(n,1);
robotGD.jacobian_dot(q,q_dot,1)

Error using *
Inner matrix dimensions must agree.

Error in DQ_kinematics/jacobian_dot (line 351)
vec_x_effector_dot = J*theta_dot(:,1:ith);

J is 8,1 and theta_dot(:,1:ith) is 2x1.

Other problematic part of the code is obj.raw_jacobian(theta,i) when i=0; This generates a 8x0 matrix with theta_dot(1:i) being 1x0.

[bvadorno]

I had tested before committing the fix and I didn't encounter any problems.

Other problematic part of the code is obj.raw_jacobian(theta,i) when i=0; This generates a 8x0 matrix with theta_dot(1:i) being 1x0.

This is not the actual behavior. When i=0, obj.raw_jacobian(theta,i) returns a 8x0 matrix and theta_dot(1:i) returns a 0 x 1 vector; therefore obj.raw_jacobian(theta,i) * theta_dot(1:i) returns a 8 x 1 vector of zeros. Did you test it by using the provided example m-file? As I can see, the error appeared in a program of yours, so I'm wondering if maybe the problem is in your program. Could you please run my example file?

Cheers,
Bruno

[juanjqo]

I am sorry, I was not precise.

There are two problems.

1. When the robot has one link. (see minimal_example.m)

Here, theta_dot(1:i) is 1x0 when i=0;

2. When is used the method jacobian_dot(q,q_dot, ith) . (see minimal_example2.m)

minimal_example.zip

[bvadorno]

Juancho, thanks a lot.

I've already fixed the problem when one uses the method jacobian_dot(q,q_dot, 1). I'm now looking into the first problem.

Bruno

[bvadorno]

Juancho, I finally fixed it. This bug was caused by lack of consistency in Matlab.

More specifically, when i = 0 and length(theta) = 1, theta(1,i) returns a 1 x 0 vector, differently from the expected behavior, which is to return a 0 x 1 matrix. Therefore, we have to deal with the case i = 0 explictly.

Please let me know if know everything works.

Cheers,
Bruno

[juanjqo]

It is working now!
Thanks for the support!

Regards,
Juancho