Tic-Tac-Toe-MinimaxAlgorithm ⭕❕❌

An implementation of Minimax AI Algorithm on Tic-Tac-Toe (or Noughts and Crosses) game. Try it: Tic-tac-toe - Minimax.

▷ What is Minimax?

Minimax is a artificial intelligence applied in two player games, such as tic-tac-toe, checkers, chess and go. This games are known as zero-sum games, because in a mathematical representation: one player wins (+1) and other player loses (-1) or both of anyone not to win (0).

▷ How does it works?

The algorithm search, recursively, the best move that leads the Max player to win or not lose (draw). It consider the current state of the game and the available moves at that state, then for each valid move it plays (alternating min and max) until it finds a terminal state (win, draw or lose).

▷ Finding the bestMove:

We shall be introducing a new function called bestMove(). This function evaluates all the available moves using minimax() and then returns the best move the maximizer can make. The pseudocode is as follows :

public Move bestMove(int[][] arr,boolean turn ){
        int best = -1000;
        Move result = new Move(-1,-1);
        
        for (int i = 0; i < arr.length; i++) {
                for (int j = 0; j < arr[i].length; j++){  
                    if(arr[i][j] == 0){
                        arr[i][j] = 2;
                        int score = minimax(arr, !turn);
                        arr[i][j] = 0;
                        if(score>best){
                            best = score;
                            result.setX(i);
                            result.setY(j);
                        }
                    }
                }
        }
        return result;
    }

▷ Minimax:

To check whether or not the current move is better than the best move we take the help of minimax() function which will consider all the possible ways the game can go and returns the best value for that move, assuming the opponent also plays optimally

The code for the maximizer and minimizer in the minimax() function is similar to findBestMove(), the only difference is, instead of returning a move, it will return a value. Here is the pseudocode :

public int minimax(int[][] arr, boolean isTurn){
        int s = checkResult(arr);
        if(s == 10) return s;
        if(s == -10) return s;
        if(checkMove(arr) == false)
            return 0;
        if (isTurn == true){
            int best = -10000;
            for (int i = 0; i < arr.length; i++) {
                for (int j = 0; j < arr[i].length; j++){
                    if(arr[i][j]==0){
                        arr[i][j] =2;
                        best = Math.max(best, minimax(arr, !isTurn));
                        arr[i][j] =0;
                    }
                }
            }
            return best;
        }
        else {
            int best = 10000;
            for (int i = 0; i < arr.length; i++) {
                for (int j = 0; j < arr[i].length; j++){
                    if(arr[i][j]==0){
                        arr[i][j] =1;
                        best = Math.min(best, minimax(arr, !isTurn));
                        arr[i][j] =0;
                    }
                }
            }
            return best;
        }
    }

▷ Checking for GameOver state:

To check whether the game is over and to make sure there are no moves left we use checkMove() function. It is a simple straightforward function which checks whether a move is available or not and returns true or false respectively. Pseudocode is as follows :

 public boolean checkMove(int[][] arr){
        for (int i = 0; i < arr.length; i++) {
                for (int j = 0; j < arr[i].length; j++) {
                    if(arr[i][j]==0){
                        return true;
                    }      
            }
        } 
         return false;
    }

▷ Implements MouseListener:

public void mousePressed(MouseEvent e) {
            for (int i = 0; i < arBT.length; i++) {
                for (int j = 0; j < arBT[i].length; j++) {
                    if (e.getButton() == 1 && e.getSource()==arBT[i][j] && turn == false && arrEnd[i][j] == false){
                        arBT[i][j].setText("X");
                        arr[i][j] = 1;
                        arrEnd[i][j] = true;
                        turn = true;
                        btReset.setEnabled(true);
                    }             
                } 
            }
            if(turn == true && checkMove(arr)==true){
                Move p = bestMove(arr, turn);
                int i = p.getX();
                int j = p.getY();
                arBT[i][j].setText("O");
                arrEnd[i][j]=true;
                arr[i][j] = 2;
                turn = false;
            }
            int check = checkResult(arr);
            if(check == 10 && endGame == false){
                JOptionPane.showConfirmDialog(null, "Máy Thắng !!!","Kết thúc trò chơi",JOptionPane.DEFAULT_OPTION);
                end();
                endGame = true;
            }else if(check == -10 && endGame == false){
                JOptionPane.showConfirmDialog(null, "Người Thắng !!!","Kết thúc trò chơi",JOptionPane.DEFAULT_OPTION);
                end();
                endGame = true;
            }
            if(endGame == false){
                if(checkMove(arr) == false){
                    JOptionPane.showConfirmDialog(null, "Hoà nhau !!!","Kết thúc trò chơi",JOptionPane.DEFAULT_OPTION);
                endGame = true;
                }
            }
        }

▷ Explanation :

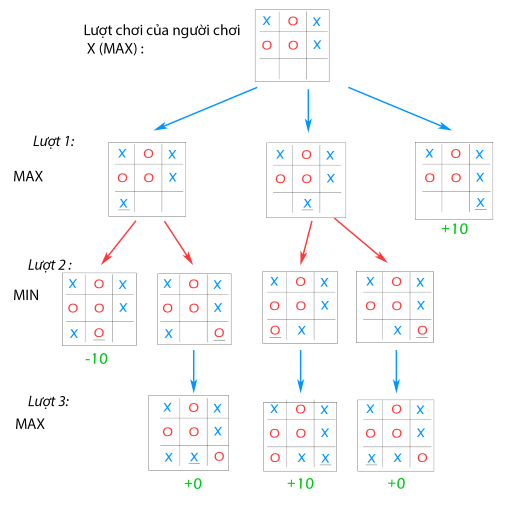
This image depicts all the possible paths that the game can take from the root board state. It is often called the Game Tree.

As we can see in the picture above, the current state of the game is on player X's turn to represent MAX. We temporarily set the value of MAX when the game wins for X = +10 and MIN when the game loses for X = -10 and when the game is drawn = 0.

Now in turn 1, MAX can go 1 of 3 moves as shown. So how to choose 1 of the 3 countries which is the best to go. We rely on the value of each country to choose the best country, as here those 3 nodes belong to the MAX class, so choose the largest value. We start finding the value of each of those nodes. In the MAX layer in turn 1, we have nodes 1,2,3 numbered from left to right as shown. Our node 3 is already a leaf node (X win game ) and has a value of +10. And 2 nodes 1,2, do not know its value at turn 1, so we rely on the value of the child nodes to determine the value and equal to the minimum value of the child nodes in the MIN layer at turn 2. So on Continue like this until we meet a leaf node, then from that leaf node we infer and we calculate that node 1 has a value of -10 and node 2 is 0. So the best move here is like node 3 has a value of -10. maximum value is +10.

▷ Author: F.O.G_ntp(nguyenthanhphong)