给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回答案。
- 示例1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
- 示例2:
输入:nums = [3,2,4], target = 6
输出:[1,2]`
- 示例3:
输入:nums = [3,3], target = 6
输出:[0,1]
- 返回一对数组中满足target的值的下标
public class Solution1 {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < nums.length; i++) {
if(map.containsKey(target - nums[i]))
return new int[] {map.get(target - nums[i]), i};
else map.put(nums[i], i);
}
return new int[0];
}
}将nums的下标存储为map的值,nums的值存储为map的键,查找map中是否含有满足target - nums[i]的键, 有则返回对应的下标对,不含有则将值加入map中。
- 返回所有数组中满足target的值的下标
public class Solution2 {
public List<int[]> twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
List<int[]> result = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement)) {
int j = map.get(complement);
if (j != i) {
result.add(new int[]{j, i});
}
}
map.put(nums[i], i);
}
return result.isEmpty() ? null : result;
}
}同上,但是将所有满足条件的下标对加入到List中
给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照逆序的方式存储的,并且每个节点只能存储一位数字。 请你将两个数相加,并以相同形式返回一个表示和的链表。你可以假设除了数字0之外, 这两个数都不会以0开头。
- 示例1:
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807
- 示例2:
输入:l1 = [0], l2 = [0]
输出:[0]
- 示例3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode head = new ListNode();
ListNode p = head;
int carry = 0;
while(l1 != null || l2 != null) {
if(l1 != null) {
carry += l1.val;
l1 = l1.next;
}
if(l2 != null) {
carry += l2.val;
l2 = l2.next;
}
p.next = new ListNode(carry % 10);
p = p.next;
carry = carry / 10;
}
if(carry > 0)
p.next = new ListNode(carry);
return head.next;
}
}从个位开始,将加起来的值取余后放在节点中,除10后进位。
当l1和l2长度不相等时,最后将carry除10后再新建节点并加载链表尾端。
给定一个字符串s,请你找出其中不含有重复字符的最长子串的长度。
- 示例1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是"abc",所以其长度为3。
- 示例2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是"b",所以其长度为 1。
- 示例3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是"wke",所以其长度为3。 请注意,你的答案必须是子串的长度,"pwke"是一个子序列,不是子串。
class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
Set<Character> set = new HashSet<Character>();
int r = 0, ans = 0;
for(int i = 0; i < len; i++) {
if(i != 0)
set.remove(s.charAt(i - 1));
while(r < len && !set.contains(s.charAt(r))) {
set.add(s.charAt(r));
++r;
}
ans = Math.max(ans, r - i);
}
return ans;
}
}采用双指针,当从第0个字符开始,字符不在set中则加入到set,右指针右移。
如果右侧出现相同的字符,则左指针右移一位并将相同的字符从set中移除。
给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k、j != k, 同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。
- 示例1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
- 示例2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。
- 示例3:
输入:nums = [0,0,0]
输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。
public class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
int len = nums.length;
Arrays.Sort(nums);
for (int i = 0; i < len; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue;
int target = -nums[i];
for (int j = i + 1; j < len; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
int k = len - 1;
while (j < k && nums[j] + nums[k] > target)
k--;
if (j == k)
break;
if (nums[j] + nums[k] == target) {
List<Integer> ans = new ArrayList<>(Arrays.asList(nums[i], nums[j], nums[k]));
res.add(ans);
}
}
}
return res;
}
}给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
- 示例1:
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
- 示例2:
输入:head = [1], n = 1 输出:[]
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0, head);
ListNode prev = head;
ListNode cur = dummy;
int len = 0;
while (prev != null) {
prev = prev.next;
len++;
}
for (int i = 0; i < len - n; i++)
cur = cur.next;
cur.next = cur.next.next;
ListNode ans = dummy.next;
return ans;
}
}给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
- 示例1:
输入:s = "()[]{}" 输出:true
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
int length = s.length();
if (length % 2 != 0) {
return false;
}
char[] chars = s.toCharArray();
for (int i = 0; i < length; i++) {
if (chars[i] == '(') {
stack.push('(');
} else if (chars[i] == '[') {
stack.push('[');
} else if (chars[i] == '{') {
stack.push('{');
} else {
if (stack.isEmpty()) {
return false;
} else {
Character pop = stack.peek();
if (chars[i] == ')' && pop == '(' || chars[i] == ']' && pop == '[' || chars[i] == '}' && pop == '{') {
stack.pop();
} else {
return false;
}
}
}
}
return stack.isEmpty();
}
}将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
- 示例1:
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
- 示例2:
输入:l1 = [], l2 = [] 输出:[]
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode p1 = list1, p2 = list2;
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
while (p1 != null && p2 != null) {
if (p1.val <= p2.val) {
cur.next = p1;
p1 = p1.next;
} else {
cur.next = p2;
p2 = p2.next;
}
cur = cur.next;
}
cur.next = (p1 == null) ? p2 : p1;
return dummy.next;
}
}public class Solution1 {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if (list1 == null) {
return list2;
} else if (list2 == null) {
return list1;
} else if (list1.val < list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
} else {
list2.next = mergeTwoLists(list1, list2.next);
return list2;
}
}
}递归
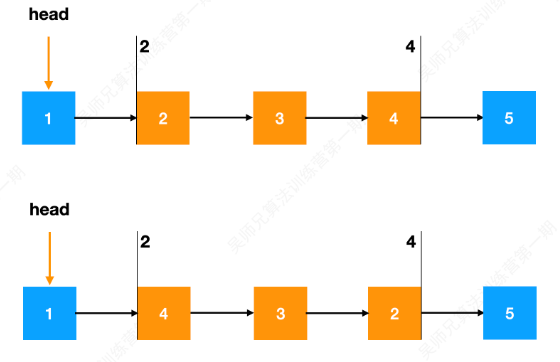
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
- 示例1:
输入:head = [1,2,3,4] 输出:[2,1,4,3]
- 示例2:
输入:head = [] 输出:[]
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy;
while (cur.next != null && cur.next.next != null) {
ListNode first = cur.next;
ListNode second = first.next;
ListNode third = second.next;
cur.next = second;
second.next = first;
first.next = third;
cur = first;
}
return dummy.next;
}
}给你一个非严格递增排列的数组 nums ,请你原地删除重复出现的元素,使每个元素只出现一次,返回删除后数组的新长度。
元素的相对顺序应该保持一致 。然后返回nums中唯一元素的个数。
- 示例1:
输入:nums = [1, 1, 2]
输出:2, nums = [1, 2, _]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
- 示例2:
输入:nums = [0, 0, 1, 1, 1, 2, 2, 3, 3, 4] 输出:5, nums = [0, 1, 2, 3, 4]
解释:函数应该返回新的长度 5 ,并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
class Solution {
public int removeDuplicates(int[] nums) {
if (nums.length == 0) return 0;
int slow = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != nums[slow]) {
nums[++slow] = nums[i];
}
}
return slow + 1;
}
}给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
- 示例1:
输入:nums = [3, 2, 2, 3], val = 3
输出:2, nums = [2, 2, _, _] 解释:你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
- 示例2:
输入:nums = [0, 1, 2, 2, 3, 0, 4, 2], val = 2 输出:5, nums = [0, 1, 4, 0, 3, _, _, _] 解释:你的函数应该返回 k = 5,并且 nums 中的前五个元素为 0,0,1,3,4。 注意这五个元素可以任意顺序返回。
class Solution {
public int removeElement(int[] nums, int val) {
if (nums == null || nums.length == 0) return 0;
int left = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != val) {
nums[left] = nums[i];
left++;
}
}
return left;
}
}给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
class Solution {
public void rotate(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[] ans = new int[m * n];
int k = 0;
for (int i = m - 1; i >= 0; i--) {
for (int j = 0; j < n; j++) {
ans[k++] = matrix[i][j];
}
}
k = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
matrix[j][i] = ans[k++];
}
}
//1 2 3 7 4 1
//4 5 6 8 5 2
//7 8 9 9 6 3
}
}先将数组按照从最后一行到第一行写入数组,再将数组按照先列后行写入原数组。
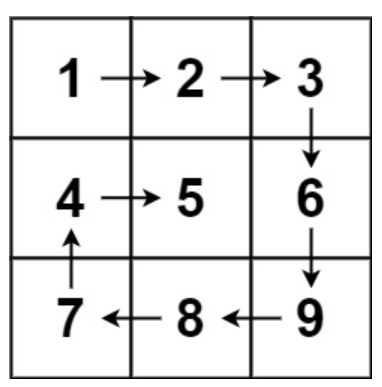
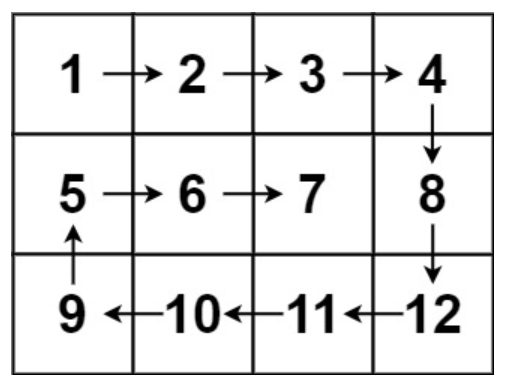
给你一个m行n列的矩阵matrix,请按照顺时针螺旋顺序,返回矩阵中的所有元素。
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]
- 按层模拟
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> res = new ArrayList<>();
int m = matrix.length, n = matrix[0].length;
int top = 0, left = 0;
int bottom = m -1, right = n - 1;
while (top <= bottom && left <= right) {
for (int j = left; j <= right; j++)
res.add(matrix[top][j]);
top++;
for (int i = top; i <= bottom; i++)
res.add(matrix[i][right]);
right--;
if (left <= right && top <= bottom) {
for (int j = right; j >= left; j--)
res.add(matrix[bottom][j]);
bottom--;
for (int i = bottom; i >= top; i--)
res.add(matrix[i][left]);
left++;
}
}
return res;
//1 2 3 4
//5 6 7 8
//9 10 11 12
//13 14 15 16
}
}设置四个边界top, bottom, left, right,从左到右:(top, left)到(top, right),然后top++表示进入下一层,当前已遍历1,2,3,4;从上到下:(top, right)到(bottom, right),然后right++,当前已遍历8,12,16;由于top和right已更新,判断是否越过边界。从右到左:(bottom, right)到(bottom, left),然后bottom--,当前已遍历15,14,13;从下到上:(bottom, left)到(top, left),然后left++,当前已遍历9,4。
- 模拟
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> res = new ArrayList<Integer>();
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return res;
int m = matrix.length, n = matrix[0].length;
boolean[][] visited = new boolean[m][n];
int row = 0, col = 0;
int total = m * n;
int index = 0;
int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
for (int i = 0; i < total; i++) {
res.add(matrix[row][col]);
visited[row][col] = true;
int nextRow = row + directions[index][0], nextCol = col + directions[index][1];
if (nextRow < 0 || nextRow >= m || nextCol < 0 || nextCol >= n || visited[nextRow][nextCol]) {
index = (index + 1) % 4;
}
row += directions[index][0];
col += directions[index][1];
}
return res;
}
}设定一个方向二位数组,分别表示向右,向下,向左,向上,从(0, 0)开始,逐次向右,每次计算nextRow和nextCol,判断是否越界和是否访问过,是则index++并且对4取余,然后row和col变换后进入下一次循环。
给你一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
输入:n = 3 输出:[1,2,3,6,9,8,7,4,5]
- 示例2:
输入: n = 1 输出: [[1]]
- 按层模拟
class Solution {
public int[][] generateMatrix(int n) {
int[] nums = new int[n * n];
int[][] matrix = new int[n][n];
for (int i = 0; i < n * n; i++)
nums[i] = i + 1;
int index = 0;
int top = 0, left = 0;
int bottom = n - 1, right = n - 1;
while (left <= right && top <= bottom) {
for (int i = left; i <= right; i++) {
matrix[top][i] = nums[index++];
}
top++;
for (int i = top; i <= bottom; i++) {
matrix[i][right] = nums[index++];
}
right--;
if (left <= right && top <= bottom) {
for (int i = right; i >= left; i--) {
matrix[bottom][i] = nums[index++];
}
bottom--;
for (int i = bottom; i >= top; i--) {
matrix[i][left] = nums[index++];
}
left++;
}
}
return matrix;
}
}如leetcode54
- 模拟
class Solution {
public int[][] generateMatrix(int n) {
int[] nums = new int[n * n];
int[][] matrix = new int[n][n];
for (int i = 0; i < n * n; i++)
nums[i] = i + 1;
int index = 0, total = n * n;
int row = 0, col = 0;
boolean[][] visited = new boolean[n][n];
int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
for (int i = 0; i < total; i++) {
matrix[row][col] = nums[i];
visited[row][col] = true;
int nextRow = row + directions[index][0], nextCol = col + directions[index][1];
if (nextRow < 0 || nextRow >= n || nextCol < 0 || nextCol >= n || visited[nextRow][nextCol]) {
index = (index + 1) % 4;
}
row += directions[index][0];
col += directions[index][1];
}
return matrix;
}
}设定一个方向二位数组,分别表示向右,向下,向左,向上,从(0, 0)开始,逐次向右,每次计算nextRow和nextCol, 判断是否越界和是否访问过,是则index++并且对4取余,然后row和col变换后进入下一次循环。
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。
- 示例1:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
- 示例2:
输入:digits = [4,3,2,1]
输出:[4,3,2,2] 解释:输入数组表示数字 4321。
- 示例3:
输入:digits = [9] 输出:[1,0] 解释:输入数组表示数字 9。加 1 得到了 9 + 1 = 10。因此,结果应该是 [1,0]。
public class Solution {
public int[] plusOne(int[] digits) {
for (int i = digits.length - 1; i >= 0; i--) {
if (digits[i] < 9) {
digits[i]++;
return digits;
}
digits[i] = 0;
}
int[] newDigits = new int[digits.length + 1];
newDigits[0] = 1;
return newDigits;
}
}给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 '/' 开头),请你将其转化为 更加简洁的规范路径。
在 Unix 风格的文件系统中规则如下:
一个点 '.' 表示当前目录本身。 此外,两个点 '..' 表示将目录切换到上一级(指向父目录)。 任意多个连续的斜杠(即,'//' 或 '///')都被视为单个斜杠 '/'。 任何其他格式的点(例如,'...' 或 '....')均被视为有效的文件/目录名称。 返回的 简化路径 必须遵循下述格式:
始终以斜杠 '/' 开头。 两个目录名之间必须只有一个斜杠 '/' 。 最后一个目录名(如果存在)不能 以 '/' 结尾。 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 '.' 或 '..')。 返回简化后得到的 规范路径 。
- 示例1:
输入:path = "/home/" 输出:"/home"
- 示例2:
输入:path = "/home/user/Documents/../Pictures" 输出:"/home/user/Pictures"
class Solution {
public String simplifyPath(String path) {
String[] strings = path.split("/");
Stack<String> stack = new Stack<>();
Stack<String> tmpstack = new Stack<>();
for (String string : strings) {
if (string.isEmpty() || string.equals(".")) {
continue;
}
if (!string.equals("..")) {
stack.push(string);
} else if (!stack.isEmpty()) {
stack.pop();
}
}
while (!stack.isEmpty()) {
tmpstack.push(stack.pop());
}
StringBuilder sb = new StringBuilder();
if (tmpstack.isEmpty()) {
sb.append('/');
} else {
while (!tmpstack.isEmpty()) {
sb.append('/');
sb.append(tmpstack.pop());
}
}
return sb.toString();
}
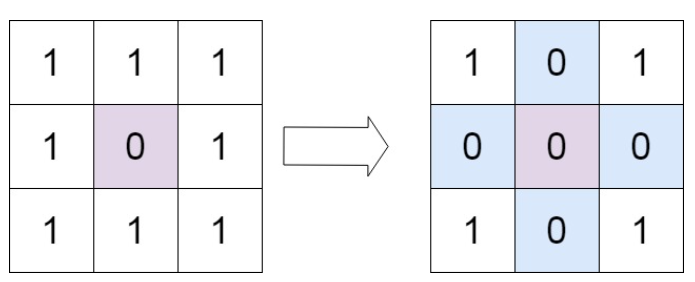
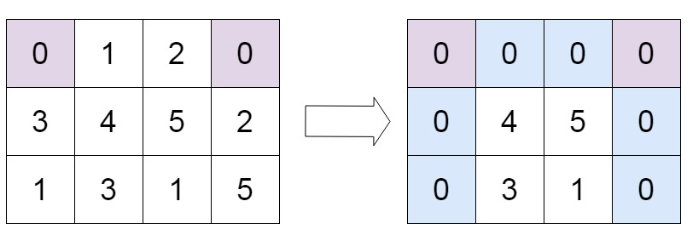
}给定一个m * n的矩阵,如果一个元素为0,则将其所在行和列的所有元素都设为0。请使用原地算法。
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
- 暴力解法:
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[][] ans = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
ans[i][j] = matrix[i][j];
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (ans[i][j] == 0) {
for (int k = 0; k < m; k++) {
matrix[k][j] = 0;
}
for (int k = 0; k < n; k++) {
matrix[i][k] = 0;
}
}
}
}
}
}- 使用记录数组:
public class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
boolean[] row = new boolean[m];
boolean[] col = new boolean[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
row[i] = col[j] = true;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (row[i] || col[j]) {
matrix[i][j] = 0;
}
}
}
}
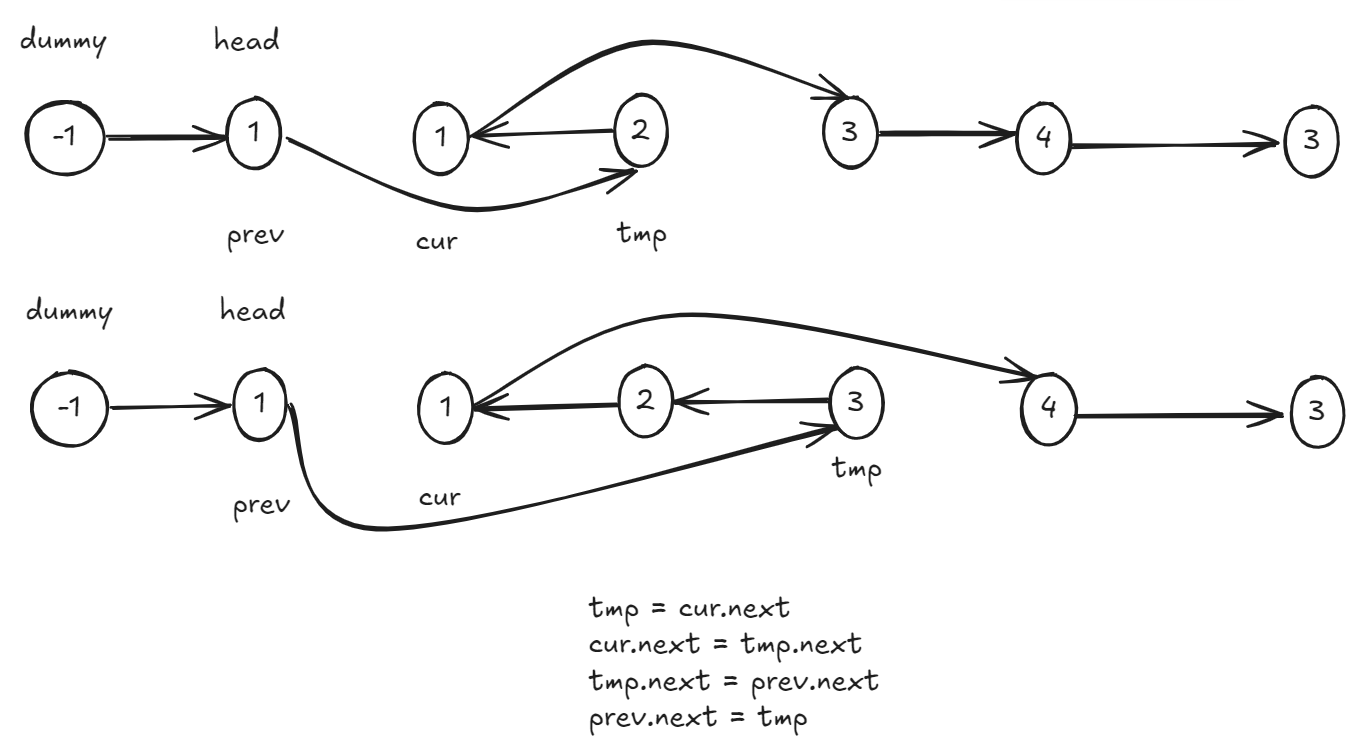
}给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
- 示例1
输入:head = [1,2,3,4,5], left = 2, right = 4 输出:[1,4,3,2,5]
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
ListNode dummy = new ListNode(-1, head);
ListNode prev = dummy;
ListNode cur = head;
for (int i = 0; i < left - 1; i++) {
cur = cur.next;
prev = prev.next;
}
for (int i = 0; i < right - left; i++) {
ListNode tmp = cur.next;
cur.next = tmp.next;
tmp.next = prev.next;
prev.next = tmp;
}
return dummy.next;
}
}给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。 请你计算该表达式。返回一个表示表达式值的整数。
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if (isNumber(token)) {
stack.push(Integer.parseInt(token));
} else {
int a = stack.pop();
int b = stack.pop();
switch (token) {
case "+": stack.push(a + b); break;
case "-": stack.push(b - a); break;
case "*": stack.push(a * b); break;
case "/": stack.push(b / a); break;
}
}
}
return stack.pop();
}
private static boolean isNumber(String str) {
try {
Integer.parseInt(str);
return true;
} catch (NumberFormatException e) {
return false;
}
}
}设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。 void push(int val) 将元素val推入堆栈。 void pop() 删除堆栈顶部的元素。 int top() 获取堆栈顶部的元素。 int getMin() 获取堆栈中的最小元素。
输入:["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]] 输出:[null,null,null,null,-3,null,0,-2] 解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
class MinStack {
Stack<Integer> stack;
Stack<Integer> minStack;
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int val) {
if (minStack.isEmpty() || val <= minStack.peek()) {
minStack.push(val);
}
stack.push(val);
}
public void pop() {
if (stack.peek().equals(minStack.peek())) {
minStack.pop();
}
stack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
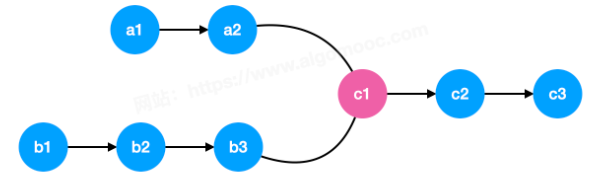
*/编写一个程序,找到两个单链表相交的起始节点。
在节点 c1 开始相交。
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> set = new HashSet<>();
ListNode cur = headA;
while (cur != null) {
set.add(cur);
cur = cur.next;
}
cur = headB;
while (cur != null) {
if (set.contains(cur)) {
return cur;
}
cur = cur.next;
}
return null;
}
}public class Solution1 {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode a = headA;
ListNode b = headB;
while (a != b) {
a = a == null ? headB : a.next;
b = b == null ? headA : b.next;
}
return a;
}
}给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
- 示例1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释: 向右轮转 1 步: [7,1,2,3,4,5,6],向右轮转 2 步: [6,7,1,2,3,4,5],向右轮转 3 步: [5,6,7,1,2,3,4]
class Solution {
public void rotate(int[] nums, int k) {
int length = nums.length;
k = k % length;
int[] nums1 = new int[length];
for (int i = 0; i < k; i++) {
nums1[i] = nums[length - k + i] ;
}
for (int j = k; j < length; j++) {
nums1[j] = nums[j - k];
}
System.arraycopy(nums1, 0, nums, 0, length);
}
}记住最后将临时数组写回原数组。
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
- 示例1:
输入: head = [1,2,6,3,4,5,6], val = 6 输出: [1,2,3,4,5]
class Solution {
public ListNode removeElements(ListNode head, int val) {
if (head == null) return null;
ListNode dummy = new ListNode(0, head);
ListNode prev = dummy;
while (prev.next != null) {
if (prev.next.val == val) {
prev.next = prev.next.next;
} else {
prev = prev.next;
}
}
return dummy.next;
}
}public class Solution2 {
public ListNode removeElements(ListNode head, int val) {
if (head == null) return null;
ListNode dummy = new ListNode(-1, head);
ListNode prev = dummy;
ListNode cur = head;
while (cur != null) {
if (cur.val == val) {
prev.next = cur.next;
} else {
prev = cur;
}
cur = cur.next;
}
return dummy.next;
}
}public class Solution1 {
public ListNode removeElements(ListNode head, int val) {
if (head == null) return null;
head.next = removeElements(head.next, val);
return head.val == val ? head.next : head;
}
}给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
- 示例1:
输入:s = "1 + 1" 输出:2
- 示例2:
输入:s = "(1+(4+5+2)-3)+(6+8)" 输出:23
class Solution {
public int calculate(String s) {
Stack<Integer> stack = new Stack<>();
int sign = 1;
int count = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
int tmp = c - '0';
while (i + 1 < s.length() && Character.isDigit(s.charAt(i + 1))) {
i++;
tmp = tmp * 10 + s.charAt(i) - '0';
}
count = count + tmp * sign;
} else if (c == '+') {
sign = 1;
} else if (c == '-') {
sign = -1;
} else if (c == '(') {
stack.push(count);
stack.push(sign);
count = 0;
sign = 1;
} else if (c == ')') {
int topSign = stack.pop();
int topNum = stack.pop();
count = topNum + count * topSign;
}
}
return count;
}
}Character.isDigit(s.charAt(i + 1) 注意不要使用++i,因为会改变i的值。
有一个单链表的 head,我们想删除它其中的一个节点 node。给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。
- 示例1:
输入: head = [4,5,1,9], node = 5 输出: [4,1,9]
class Solution {
public void deleteNode(ListNode node) {
node.val = node.next.val;
node.next = node.next.next;
}
}给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
- 示例1:
输入:nums = [1,2,3,4] 输出:[24,12,8,6]
- 示例2:
输入:nums = [-1,1,0,-3,3] 输出:[0,0,9,0,0]
class Solution {
public int[] productExceptSelf(int[] nums) {
int tmp = 1;
int[] ans = new int[nums.length];
int[] left = new int[nums.length];
int[] right = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
if (i > 0)
left[i] = left[i - 1] * nums[i - 1];
else
left[i] = tmp;
}
for (int j = nums.length - 1; j >= 0; j--) {
if (j < nums.length - 1)
right[j] = right[j + 1] * nums[j + 1];
else
right[j] = tmp;
}
for (int k = 0; k < nums.length; k++) {
ans[k] = left[k] * right[k];
}
return ans;
}
}由于时间复杂度为O(n),所以不能使用双重循环。
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
- 示例1:
输入:nums = [0,1,0,3,12] 输出:[1,3,12,0,0]
public class Solution {
public void moveZeroes(int[] nums) {
int length = nums.length;
int cur = 0;
for (int i = 0; i < length; i++) {
if (nums[i] != 0) {
nums[cur++] = nums[i];
}
}
for (int i = cur; i < length; i++) {
nums[i] = 0;
}
}
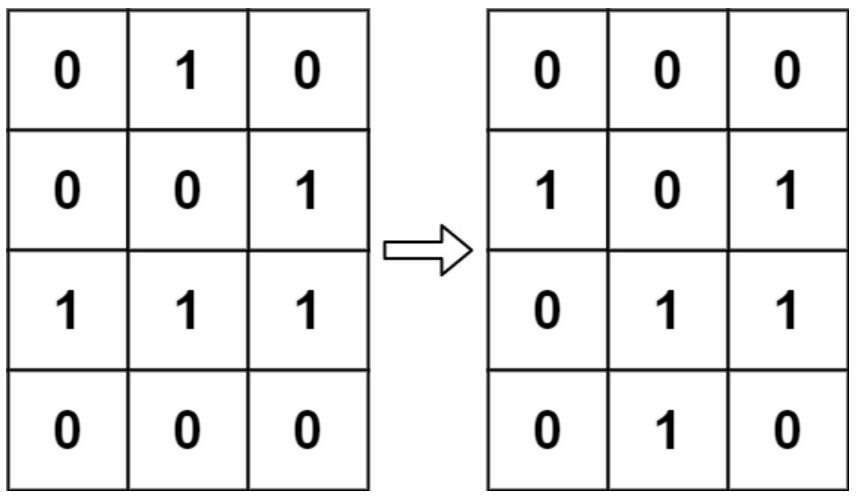
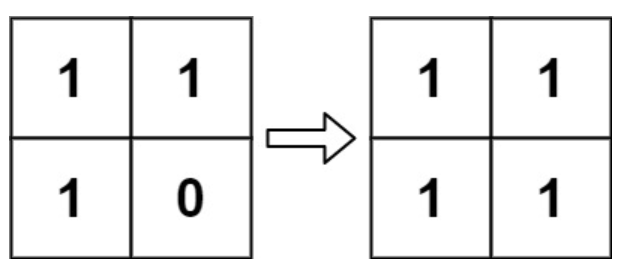
}给定一个包含m * n个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态:1即为活细胞(live),或0即为死细胞dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活; 下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你m * n网格面板board的当前状态,返回下一个状态。
给定当前board的状态,更新board到下一个状态。
注意你不需要返回任何东西。
输入:board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] 输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
输入:board = [[1,1],[1,0]] 输出:[[1,1],[1,1]]
class Solution {
public void gameOfLife(int[][] board) {
int m = board.length, n = board[0].length;
int tmp = 0;
int[][] newBoard = new int[m][n];
int[][] directions = {{-1, -1}, {0, -1}, {-1, 0}, {0, 1}, {1, 0}, {1, 1}, {-1, 1}, {1, -1}};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
newBoard[i][j] = board[i][j];
}
}
for (int i = 0; i < newBoard.length; i++) {
for (int j = 0; j < newBoard[0].length; j++) {
if (newBoard[i][j] == 1) {
for (int[] direction : directions) {
int x = i + direction[0];
int y = j + direction[1];
if (x < 0 || y < 0 || x >= m || y >= n)
continue;
if (newBoard[x][y] == 1)
tmp++;
}
if (tmp < 2 || tmp >3)
board[i][j] = 0;
tmp = 0;
} else {
for (int[] direction : directions) {
int x = i + direction[0];
int y = j + direction[1];
if (x < 0 || y < 0 || x >= m || y >= n)
continue;
if (newBoard[x][y] == 1)
tmp++;
}
if (tmp == 3)
board[i][j] = 1;
tmp = 0;
}
}
}
}
}给定一个方向数组,首先遍历矩阵中每一个元素,对于每个元素通过方向数组判断它周围的8个元素。
给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别分组,保持它们原有的相对顺序,然后把偶数索引节点分组连接到奇数索引节点分组之后,返回重新排序的链表。 第一个节点的索引被认为是 奇数 , 第二个节点的索引为 偶数 ,以此类推。
- 示例1:
输入:head = [1,2,3,4,5] 输出:[1,3,5,2,4]
class Solution {
public ListNode oddEvenList(ListNode head) {
if (head == null || head.next == null) return head;
ListNode dummy = new ListNode(-1, head);
ListNode prev = head;
ListNode cur = head.next;
ListNode tmp = head.next;
while (tmp != null && tmp.next != null) {
prev.next = prev.next.next;
tmp.next = tmp.next.next;
prev = prev.next;
tmp = tmp.next;
}
prev.next = cur;
return dummy.next;
}
}给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
- 示例1:
输入: s = "3[a]2[bc]" 输出: "aaabcbc"
- 示例2:
输入: s = "3[a2[c]]" 输出: "accaccacc"
class Solution {
public String decodeString(String s) {
Stack<Integer> stack1 = new Stack<>();
Stack<StringBuilder> stack2 = new Stack<>();
int tmp = 0;
StringBuilder res = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (Character.isDigit(ch)) {
tmp = tmp * 10 + ch - '0';
} else if (ch >= 'a' && ch <= 'z') {
res.append(ch);
} else if (ch == '[') {
stack1.push(tmp);
stack2.push(res);
tmp = 0;
res = new StringBuilder();
} else if (ch == ']') {
int count = stack1.pop();
StringBuilder out = stack2.pop();
for (int j = 0; j < count; j++) {
out.append(res.toString());
}
res = out;
}
}
return res.toString();
}
}public class Solution1 {
public String decodeString(String s) {
Stack<Integer> numStack = new Stack<>();
Stack<String> strStack = new Stack<>();
int tmp = 0;
String res = "";
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
tmp = tmp * 10 + c - '0';
} else if (c == '[') {
numStack.push(tmp);
strStack.push(res);
res = "";
tmp = 0;
} else if (c == ']') {
StringBuilder ans = new StringBuilder(strStack.pop());
int count = numStack.pop();
for (int j = 0; j < count; j++) { //res = c stack.pop() = a
ans.append(res);
}
res = ans.toString();
} else {
res += c;
}
}
return res;
}
}给定一个二进制数组 nums , 计算其中最大连续 1 的个数。
- 示例1:
输入:nums = [1,1,0,1,1,1] 输出:3 解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.
- 示例2:
输入:nums = [1,0,1,1,0,1] 输出:2
public class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int maxCount = 0;
int count = 0;
for (int num : nums) {
if (num == 1) {
count++;
} else {
maxCount = Math.max(maxCount, count);
count = 0;
}
}
maxCount = Math.max(maxCount, count);
return maxCount;
}
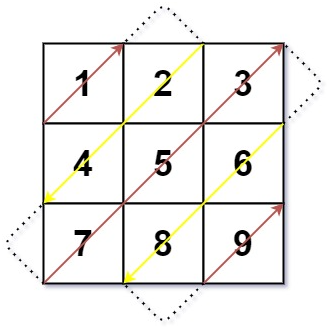
}给你一个大小为 m x n 的矩阵 mat ,请以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。
输入:mat = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,4,7,5,3,6,8,9]
- 示例2:
输入:mat = [[1,2],[3,4]] 输出:[1,2,3,4]
class Solution {
public int[] findDiagonalOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0) return new int[0];
int m = matrix.length, n = matrix[0].length;
int[] result = new int[m * n];
int row = 0, col = 0, direction = 0;
int index = 0;
while (index < m * n) {
result[index++] = matrix[row][col];
if (direction == 0) { // Up-right direction
if (col == n - 1) {
row++;
direction = 1;
} else if (row == 0) {
col++;
direction = 1;
} else {
row--;
col++;
}
} else { // Down-left direction
if (row == m - 1) {
col++;
direction = 0;
} else if (col == 0) {
row++;
direction = 0;
} else {
row++;
col--;
}
}
}
return result;
}
//1 2 3 4
//5 6 7 8
//9 10 11 12
//13 14 15 16
}Up-right direction = 0为下一步向右上方,例如从1到2,此时col++。当direction=0,矩阵为3 * 3,例如从3到7, 此时col = n - 1,则row应该++。若col = n - 1,但此时direction = 1,例如从4到7,此时row++,col--。 Down-left direction = 1与上同理。
给你一个整数数组 nums ,请计算数组的 中心下标 。 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。 如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。 如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
- 示例1:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3 解释: 中心下标是 3 。 左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 , 右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
- 示例2:
输入:nums = [1, 2, 3] 输出:-1 解释:数组中不存在满足此条件的中心下标。
- 示例3:
输入:nums = [2, 1, -1] 输出:0 解释: 中心下标是 0 。 左侧数之和 sum = 0 ,(下标 0 左侧不存在元素), 右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
class Solution {
public int pivotIndex(int[] nums) {
Queue<Integer> queue = new LinkedList<>();
int len = nums.length;
int count = 0;
int ans = 0;
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
ans += nums[j];
}
if (count == ans)
queue.offer(i);
ans = 0;
count += nums[i];
}
if (!queue.isEmpty())
return queue.poll();
else
return -1;
}
}暴力解法
public class Solution {
public int pivotIndex(int[] nums) {
int count = Arrays.stream(nums).sum();
int ans = 0;
for (int i = 0; i < nums.length; i++) {
if (2 * ans == count - nums[i])
return i;
ans += nums[i];
}
return -1;
}
}使用前缀和,左侧和为 sum,右侧和为 total - sum - nums[i]。 如果左侧和等于右侧和,则有 sum == total - sum - nums[i],整理后得到 2 * sum + nums[i] == total。
给你单链表的头结点 head ,请你找出并返回链表的中间结点。 如果有两个中间结点,则返回第二个中间结点。
- 示例1:
输入:head = [1,2,3,4,5] 输出:[3,4,5]
class Solution {
public ListNode middleNode(ListNode head) {
ListNode pre = head, cur = head;
int length = 0;
while (pre != null) {
pre = pre.next;
length++;
}
int tmp = 0;
while (tmp < length / 2) {
cur = cur.next;
tmp++;
}
return cur;
}
}给定 有效括号字符串 s,返回 s 的 嵌套深度。嵌套深度是嵌套括号的 最大 数量。
- 示例1:
输入: s = "(1+(2*3)+((8)/4))+1" 输出: 3 解释: 数字 8 在嵌套的 3 层括号中。
class Solution {
public int maxDepth(String s) {
Stack<Character> stack = new Stack<>();
char[] chars = s.toCharArray();
int tmp = 0, result = 0;
for (char c : chars) {
if (c == '(') {
stack.push('c');
tmp++;
result = Math.max(result, tmp);
} else if (c == ')') {
stack.pop();
tmp--;
}
}
return result;
}
}注意字符串是有效的括号字符串,所以考虑左括号存在就加一,有括号存在就减一。