Ancestral Colorings of Perfect Binary Trees With Applications in Private Retrieval of Merkle Proofs

Quang Cao, Rinaldo Gagiano, Duy Huynh, Xun Yi, Son Hoang Dau, Phuc Lu Le, Quang-Hung Luu, Emanuele Viterbo, Yu-Chih Huang, Jingge Zhu, Mohammad M. Jalalzai, and Chen Feng. 2022.

In this paper, we develop a divide-and-conquer algorithm called Color-Splitting Algorithm (CSA) that takes ℎ as input and generates a balanced ancestral coloring for 𝑇 (ℎ) in time linear in the number of tree nodes (excluding the root) 2^(ℎ+1) − 2. In fact, this algorithm can generate not only a balanced ancestral coloring but also any ancestral coloring (color classes having heterogeneous sizes) feasible for 𝑇 (ℎ). It is worth noting that this flexibility of our algorithm establishes the existence of optimal combinatorial patterned-batch codes corresponding to the case of servers with heterogeneous storage capacities as well. At the high level, the algorithm colors two sibling nodes at a time and proceeds recursively down to the two subtrees and repeats the process while maintaining the Ancestral Property: if a color is used for a node then it will not be used for the descendants of that node. The algorithm can produce a balanced ancestral coloring for the trees: (You can find a copy of the paper here.)

T(20) = 224 milliseconds

T(21) = 453 milliseconds

T(22) = 906 milliseconds

T(23) = 1873 milliseconds

T(24) = 3743 milliseconds

T(25) = 7523 milliseconds

T(26) = 14817 milliseconds

T(27) = 30133 milliseconds

T(28) = 59436 milliseconds

T(29) = 121429 milliseconds

T(30) = 241847 milliseconds

T(31) = 490781 milliseconds (Recommended heap size 32GB)

T(32) = 978274 milliseconds (Recommended heap size 64GB)

T(33) = 1994432 milliseconds (Recommended heap size 120GB)

T(34) = 4378425 milliseconds (Recommended heap size 240GB)

Compiling CSA

Once Java and Javac are installed, to build CSA simply run:

javac CSA.java
java CSA

To build CSA with recommended max heap size simply run:

javac CSA.java
java -Xmx32g CSA

Using CSA

Take a look at the pictures below, guidelines and in CSA.java comments for how to use CSA.

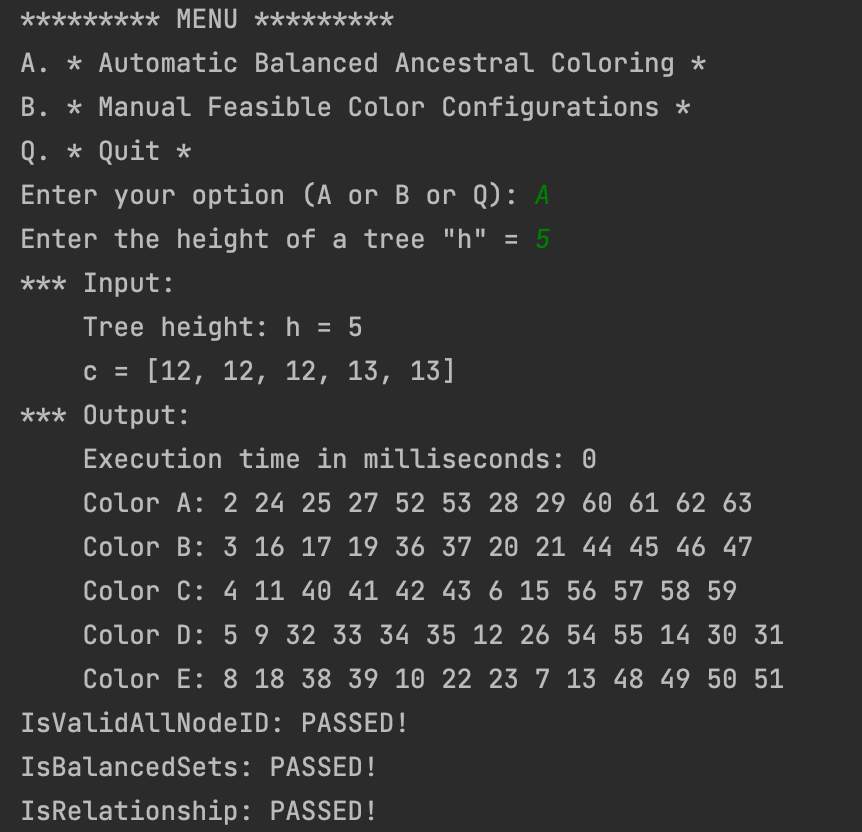
Fig 1: An example of the CSA algorithm running option A (Automatic Balanced Ancestral Coloring) when h = 5.

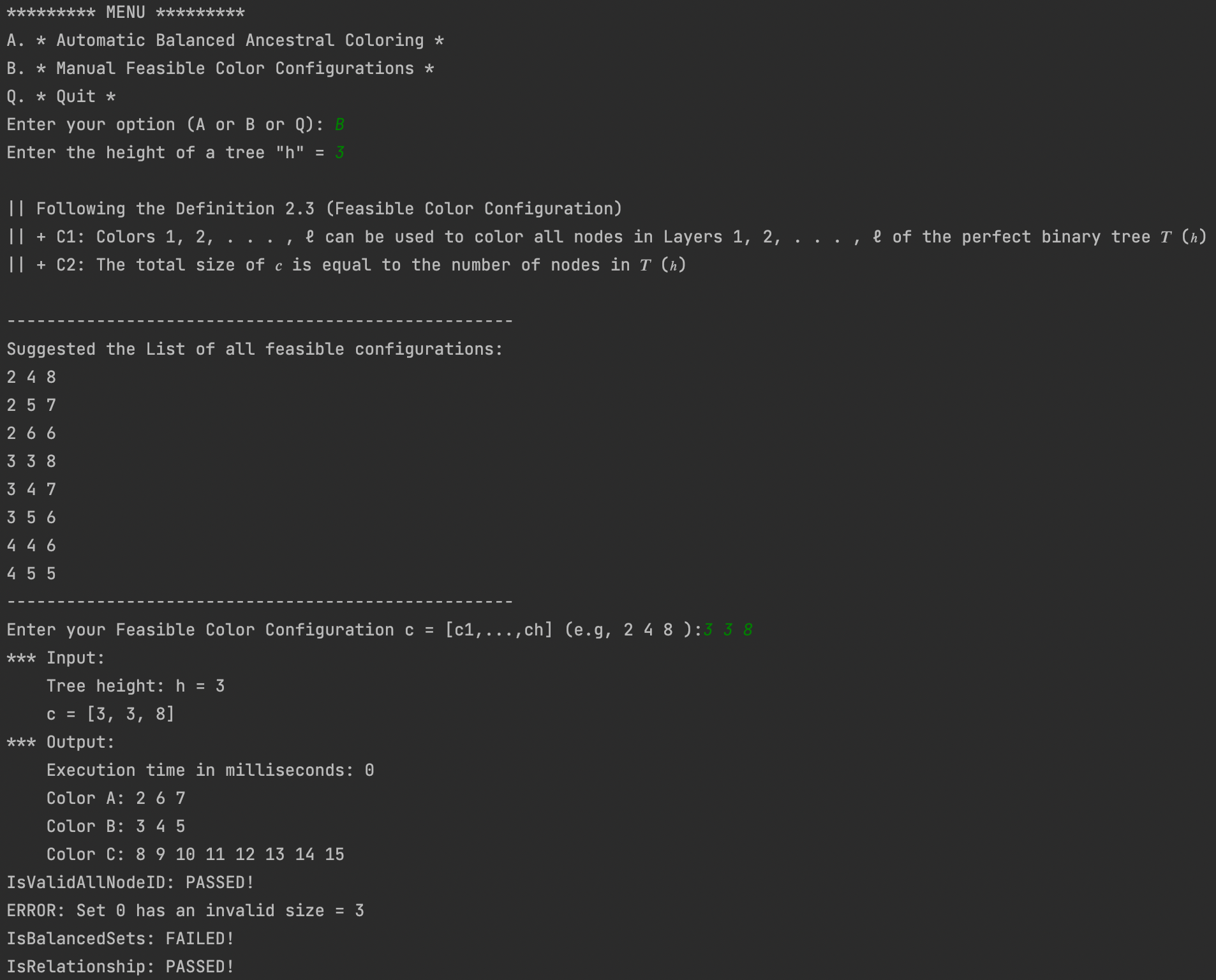
Fig 2: An example of the CSA algorithm running option B (Manual Feasible Color Configurations) with c = [3 3 8].

ACKNOWLEDGMENTS

This work was supported by the Australian Research Council through the Discovery Project under Grant DP200100731 and carried out on Oracle virtual machines, supported by Oracle for Research.