what is Big O ?

big O represent the efficiency of an algorithm

There are two different types of big O

1. Time complexity = speed, fast ,efficiency
2. Space complexity = memory use (how much space is used) (extra variable and data structure to solve the algorithm)

In real world if you have large input for your functions both time and space starts to cause problems

we use these technique as an benchmark of the algorithm (to measure how good they are)

Grading Time ans space

we dont compare it to the absolute ... we compare relative to the size of the input

linear time

Two time the input size ===>>> 2 times the time it takes

[1,2,3] = 1s(absolute) ,3(size)

[1,2,3,4,5,6] = 2s(absolute), 6(size)

we can also say that the relationship between time and input is 1 to 1 (1:1)

big O notation: o(n)

constant Space

[1,2,3] = 0(extra space) 3(size) [1,2,3,4,5,6] = 0(extra space) 6(size)

if either space and the time has no realtionship with the input than we called it a constant space

big O notation: o(1)

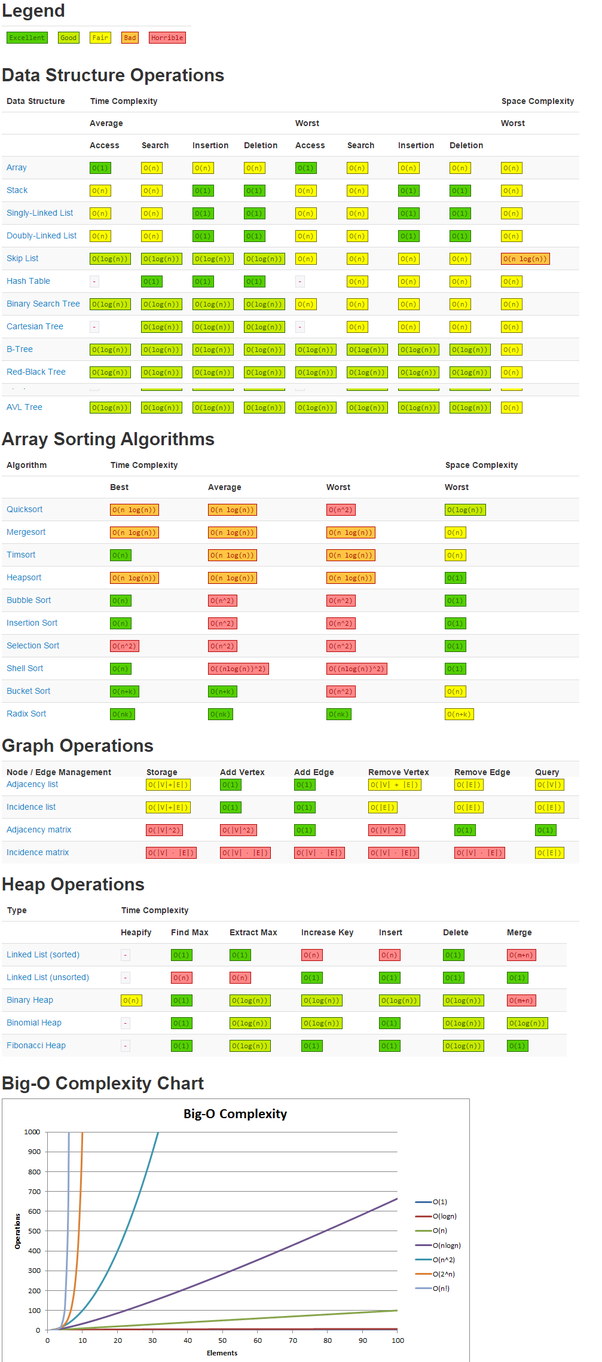
order of efficiency

example =>

most efficient ==== > O(1) "constant"

                 O(log n) "logarithmic"

                 O(n) "linear"

                 O(n log n) "linear logarithmic"

                 O(n * n) "quadratic"

least efficient ==== > O(2 ^ n ) "exponential"

code example =

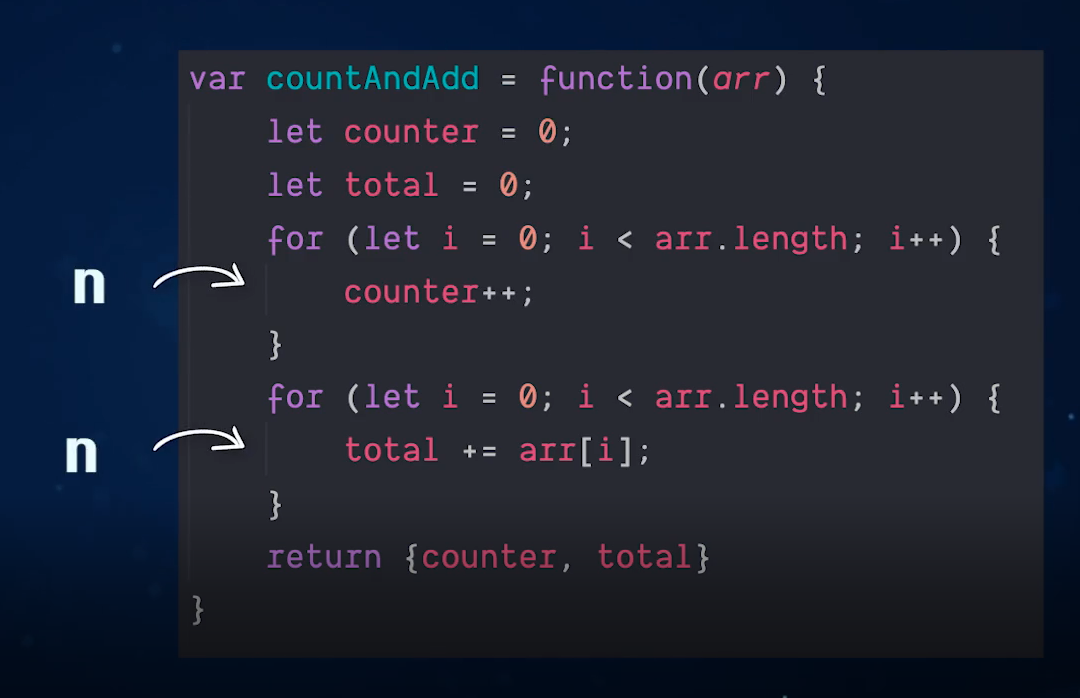
How does the input size effect the specific lines of the codes below

let length = (arr)=>{

// time and space will be constant here because int takes exactly the same space weather its 0 or 2,147,483,647

let counter = 0;

// runs n number of time where n is the arry length

/* if we go from size [1] to [1,2]

          size  1      2
     iteration  1      2

so clearly there is 1 to 1 relationship which is linear */

for (let i = 0; i <arr.length; i++){ counter++; } return counter; }

so it is taking O(1) and 0(n) thats why we simplify and take the term which is in hghest order

only keep the highest order

simplifying BIG O

-- Drop the lower order term -- Drop constant term

n + n = 2n so we drop the 2 and remaining is the notation

range of efficiency

1)best case 2) average case 3) worst case

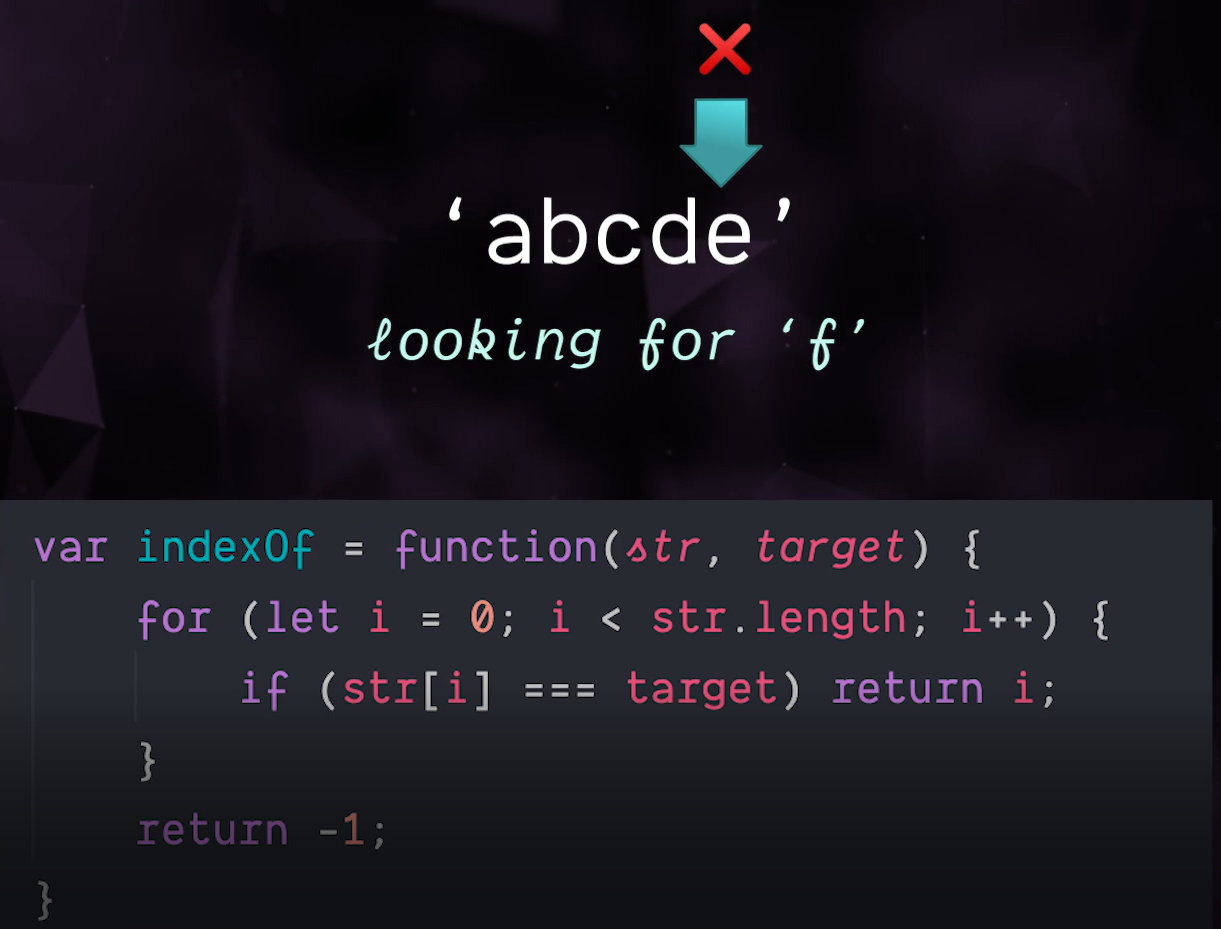
code example =

"abcde".indexof("b")

is "b" in "abcde"? if so return its index

1. best case = less amount of effort
2. average case = avg amount of effort
3. worst case = most amount of effort

Big O always takes the worst case

Hence, this "indexof" function is O(n) linear time

Data Structure

Linear Data Structure

   |
   |--> Arrays
   |
   |--> Graph
   |
   |--> Hash Tables
   |
   |--> Linked Lists
   |   |--> Singly Linked Lists
   |   |--> Doubly Linked Lists
   |
   |--> Sequential
   |   |--> Stacks
   |   |--> Queues

Non Linear Data Structure

   |
   |--> Trees
   |    |-->Binary Search Trees
   |    |   |--> Avl Tree
   |    |   |--> Red Black Tree
   |    |
   |    |--> Trie
   |    |--> Binary Heap
   |        |--> Priority Queue
   |
   |
   |--> Graph

---

A). Comparison Sort Algorithm

1).Bubble Sort

(n-1)*(n-1)
= n^2 - 2n + 1
==> O(n^2)

Pseudo code

Repeat n-1 times
  for i from 0 to n-2
  if ith and i + 1 element out of order
  swap em'

2). Selection Sort

n+(n-1)+(n-2)+....+ 1
= (n+1)*n/2 = n^2/2 + n/2
==>O(n^2)

Pseudo code

for i from 0 to n-1
  find smallest item between ith item and last item
  swap smallest item with ith item

3). Insertion Sort

(1+2+3+....(n-1))
=(n-1)*n/2
= n^2/2 - n/2
==>o(n^2)

Pseudo code

for i ← 1 to length(Array) do
    currentIndex ← i
    while currentIndex > 0 and Array[currentIndex - 1] > Array[currentIndex] do
      temp ← Array[currentIndex]
      Array[currentIndex] ← Array[currentIndex - 1]
      Array[currentIndex - 1] ← temp
      currentIndex ← currentIndex - 1
    end while
    i ← i + 1

4). Merge Sort

O(nlogn)

pseudo code

if only one item
  return
 else
  sort left half of items
  sort right half of items
  merge sorted halves

B). Non-Comparison Sort Algorithm

1). Radix Sort

---

---

---

---