Adds a DFS and a BFS solution for "The Maze"

[altay9]

Resolves #48

This solution is very important to grasp DFS and it is a kind of basis for The Maze II and The Maze III.

It is also a little bit different than the usual DFS problems as you cannot stop and change direction until you encounter a wall or the destination.

It is important to note that, you have to decide if DFS can pass over the next cell, not the current cell.

The most straightforward cases are noted in the problem statement (#48) for the first and second examples.

But, I think there is another case that is more veiled and pretty hard to see at the first glance.

I tried to draw the mentioned case:

In the above-mentioned case; you must pass at the first encounter but you have to stop after another turn of DFS (and in a different direction.)

[altay9]

[ErdemT09]

Why is the helper method called "dps" and not "dfs"?
Does it stand for something like "depth prioritized search"?

[altay9]

Why is the helper method called "dps" and not "dfs"?
Does it stand for something like "depth prioritized search"?

No no. It is just a typo. Thanks for your attention. Fixing now.

[ErdemT09]

I think using parenthesis here for the operators would make the code more readable.
As a note for those who do not know about the precedence of the operators.

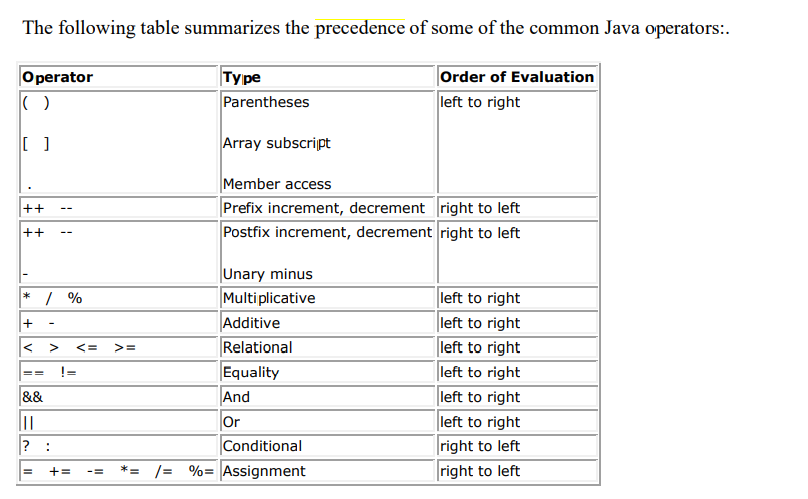
Source: http://www.math.uaa.alaska.edu/~afkjm/cs110/handouts/IfStatements.pdf

[altay9]

Nice idea to add this table.

[ErdemT09]

Let's say that we have went left from some tile. This loop implies that we will also traverse the same from left to right until we see that the right tile is already visited. Isn't this to some degree duplicate unneeded calculation or am I seeing it wrong?

[altay9]

It is duplicated but I am not sure if it is unnecessary.

Somehow we have to distinguish the above-mentioned case and the case in Example-2.

It is one of the alternative ways.

We can change it when we find a more efficient way.

[ErdemT09]

We can perhaps put a simple statement like "Don't go right" to the method call. We can wrap this up in an integer or a boolean value.

[altay9]

I will also add BFS solution. Maybe it is much more appropriate as it can prevent dead-ends more efficiently.

[altay9]

Adds BFS, refactors DFS.

[altay9]

Adds our first unit test for The Maze - DFS solution.

[ErdemT09]

Here is what I meant:

public boolean dfs(int x, int y, int arrivedFrom) {

        if (x == destination[0] && y == destination[1]) {
            return true;
        }

        visited[x][y] = true;
        boolean result = false;

           for (int i = 0; i<4; i++){
               
            if((i == 0 && arrivedFrom == 3)
            ||(i == 1 && arrivedFrom == 2)
            || (i == 2 && arrivedFrom == 1)
            || (i == 3 && arrivedFrom == 0))
            {
                continue;
            }
            int dirx = directions[i][0];
            int diry = directions[i][1];
            int nextX = x + dirx;
            int nextY = y + diry;

            while (canPass(nextX, nextY)
                    && !visited[nextX][nextY]) {
                int prx = nextX;
                int pry = nextY;
                nextX += dirx;
                nextY += diry;
                result = result || !canPass(nextX, nextY) && dfs(prx, pry, i);

            }
       }

        return result;
    }

This way, the program does not repeat itself, reducing the overall muda.

[altay9]

Here is what I meant:

Nice idea Erdem, thanks.
I am not sure what the exact run-time efficiency is, as it changes at each run: (mostly 1-2 ms)

But, it is fine to add to be more specific.

By the way, it was also very useful in The Maze II.

[ErdemT09]

In the BFS solution, we can perhaps implement the algorithm of not going back to the place we came from by changing the boolean matrix with a int, or simply byte matrix.
I am not sure, but as a note, it can be something like this:

    private final static boolean[] UNVISITED = {false, false, false, false};
    private final static boolean[] RIGHT = {true, false, false, false};
    private final static boolean[] LEFT = {false, true, false, false};
    private final static boolean[] UP = {false, false, true, false};
    private final static boolean[] DOWN = {false, false, false, true};

    private boolean[][][] visited;

We can work with BitsSet as well.

[ErdemT09]

I think the solutions are current quite fine. We can add other settings to them in the future if needed.