259. 3Sum Smaller #302
Merged
259. 3Sum Smaller #302
Conversation
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
Collaborator
Author
|
I also try adding unit tests for this problem. |
altay9
reviewed
Jun 8, 2021
|
|
||
| import java.util.Arrays; | ||
|
|
||
| public class ThreeSumSmallerIterative { |
Collaborator
There was a problem hiding this comment.
I just copy the explanation to track the code while reading it.
Resolves #55
Algorithm:
Points to notice:
- Adding 3 numbers being less than some value is equivalent to picking one of these numbers, subtracting it from the target value and the sum of the other 2 being less than target - subtracted value (
target_).- We can then sort the array, loop over it from from the lowest value to the largest, subtract the value from the target and look at the right rest of the array for pairs of suitable numbers.
- We can then start this comparison from the right next of the value. The other compared value should then be the largest value. If some largest value + the left value is smaller than
target_then all the values smaller then this right large value can be added with the left value to get a sum smaller thantarget_.- The right pointer must be always larger than the left pointer then.
- If the previous operation is successful, we can increment the left pointer to look for two sums with the number at this pointer. Remember, the array is sorted.
- We should then do this collect the possible two sum combinations each time until the loop condition is false.
- In the main loop, if we can't find any two sums at some index, that means that we won't be able to find two sums for numbers larger than it for further indices.
- We don't always need to initialize the right boundary with the size of the array. Since the numbers are always getting larger, our new first possible right pointer will either be smaller than or equal to the previous first possible. So, we can store that in a variable.
altay9
reviewed
Jun 8, 2021
| int rightBoundary; | ||
|
|
||
| public int threeSumSmaller(int[] nums, int target) { | ||
|
|
Collaborator
There was a problem hiding this comment.
It is also great, after fixing the if check:
altay9
reviewed
Jun 8, 2021
Comment on lines
+30
to
+48
| public int findTwoSumsSmaller(int start, int target) { | ||
|
|
||
| int p1 = start, p2 = rightBoundary; | ||
| int count = 0; | ||
| boolean foundBounds = false; | ||
| while (p1 < p2) { | ||
| if (nums[p1] + nums[p2] >= target) { | ||
| if (!foundBounds) { | ||
| rightBoundary--; | ||
| } | ||
| p2--; | ||
| } else { | ||
| foundBounds = true; | ||
| count += p2 - p1; | ||
| p1++; | ||
| } | ||
| } | ||
| return count; | ||
| } |
Collaborator
There was a problem hiding this comment.
Similar simplification may be done here too.
ErdemT09
commented
Jun 8, 2021
Comment on lines
+24
to
+42
| public int reduceTwoSumsSmaller(int start) { | ||
| int currTarget = target - nums[start]; | ||
| int p1 = start + 1, p2 = rightBoundary; | ||
| int count = 0; | ||
| boolean foundBounds = false; | ||
| while (p1 < p2) { | ||
| if (nums[p1] + nums[p2] >= currTarget) { | ||
| if (!foundBounds) { | ||
| rightBoundary--; | ||
| } | ||
| p2--; | ||
| } else { | ||
| foundBounds = true; | ||
| count += p2 - p1; | ||
| p1++; | ||
| } | ||
| } | ||
| return count == 0 ? 0 : count + reduceTwoSumsSmaller(start + 1); | ||
| } |
Collaborator
Author
There was a problem hiding this comment.
How do we make use of the right boundary in this? I don't think itmis being used.
altay9
approved these changes
Jun 8, 2021
Collaborator
altay9
left a comment
altay9
left a comment
There was a problem hiding this comment.
Thank you for your valuable contribution and collaboration Erdem.
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
Add this suggestion to a batch that can be applied as a single commit.
This suggestion is invalid because no changes were made to the code.
Suggestions cannot be applied while the pull request is closed.
Suggestions cannot be applied while viewing a subset of changes.
Only one suggestion per line can be applied in a batch.
Add this suggestion to a batch that can be applied as a single commit.
Applying suggestions on deleted lines is not supported.
You must change the existing code in this line in order to create a valid suggestion.
Outdated suggestions cannot be applied.
This suggestion has been applied or marked resolved.
Suggestions cannot be applied from pending reviews.
Suggestions cannot be applied on multi-line comments.
Suggestions cannot be applied while the pull request is queued to merge.
Suggestion cannot be applied right now. Please check back later.
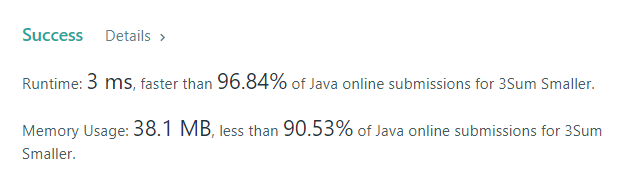
Resolves #55
Algorithm:
Points to notice:
target_).target_then all the values smaller then this right large value can be added with the left value to get a sum smaller thantarget_.