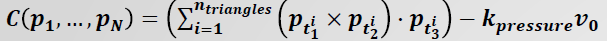-
Mass points :
- Mass 𝒎𝒊, position 𝒙𝒊, velocity 𝒗𝒊
-
Constraints :
- e.g. spring(distance) constraint
-
Just like mass spring systems
-
Main difference time stepping method
-
Operate on “proposed solution” : 𝒑𝟏,…,𝒑𝒏
-
Distance constraint (spring) : 𝑪𝒑𝒊,𝒑𝒋=𝒑𝒊−𝒑𝒋−𝒅
-
The most primitive of geometric constraints, distance based constraints restore mesh edges that extend or compress relative to their rest length
-
-
Projection
-
Task : update state 𝒑𝟏,…,𝒑𝒏so that the constraints are approximately satisfied
-
PBD uses local linearization : one constraint at a time
-
PBD use only first derivatives
-
-Main idea of PBD
-
Project constraints one by one
-
One descent step per constraint
-
Why this works better?
-
𝒑𝒊are immediately updated
-
Next linearization works with the updated state
-
-
Taylor expansion :
- 𝑪𝒑+Δ𝒑≈𝑪𝒑+𝜵𝒑𝑪𝒑∙Δ𝒑=𝟎
-
Step :
- Δ𝒑=𝝀𝜵𝒑𝑪𝒑
Putting together :
- Δ𝒑=−𝑪(𝒑)/|𝜵𝒑𝑪(𝒑)|^𝟐*𝜵𝒑𝑪𝒑
-
Important for cloth and thin shells
-
How to measure bending?
-
Simple way : cross spring
-
Drawback : interferes with in plane stretching
-
-
Constraint on volume of closed mesh
-
Assume : collisions already detected
- Simple objects : easy
-
Similar as penalty forces (but constraints)