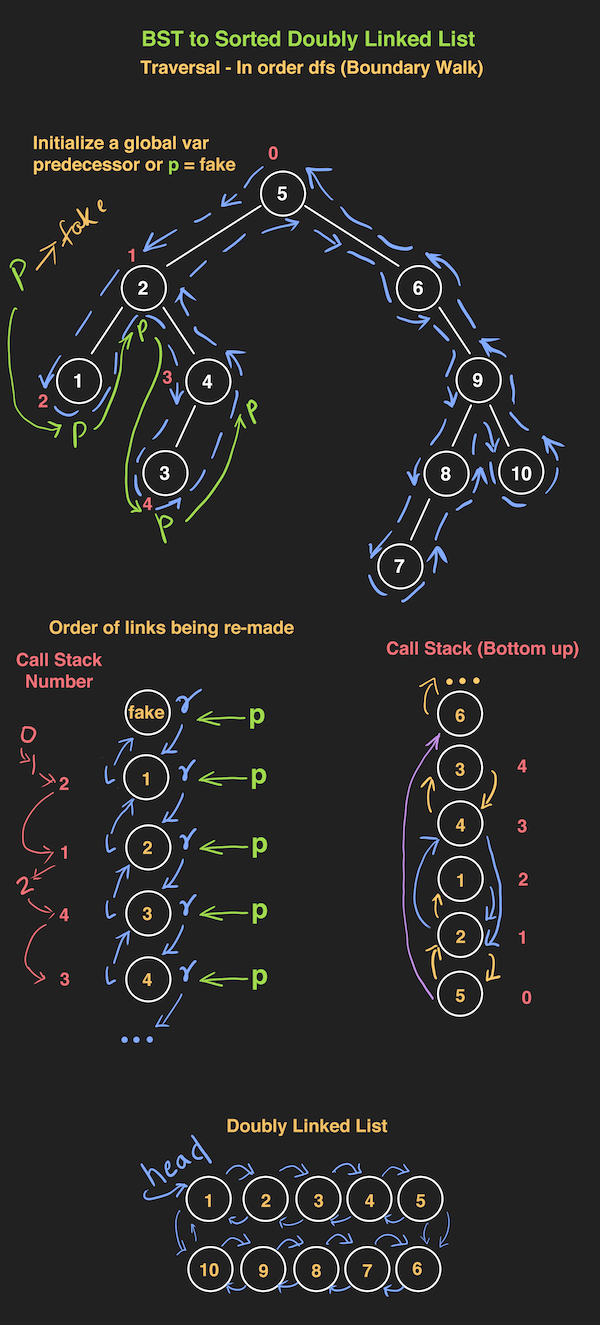
LC 0426 [M] Convert Binary Search Tree to Sorted Doubly Linked List

• this is a boundary walk, not top-down or bottom-up, because you have to keep track of the predecessor
• when you hit the left bottom, the parent will get the pred as info, then pass it back up to the right
• it's simpler to think of this as just an inorder traversal, without leaves, while keeping track of a predecessor, starting off with a dummy
• focus on the 1<->2 relationship to grasp the rest of the problem

in-order cause we want it in 1<->2<->3

---

class Solution:
    head = None
    tail = None
    
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        
        def inorder(node):
            if not node: return
            
            inorder(node.left)
            

            if not self.head: # create a starting point by just putting down the node
                self.head = node
            else: # add the node to the tail end
                node.left = self.tail
                self.tail.right = node

            self.tail = node # set the new node that was just added as the new tail
                    

            inorder(node.right)
                    
        if not root: return
                            
        inorder(root)
                    
        # link head + tail at the end to complete the loop
        self.head.left = self.tail
        self.tail.right = self.head
        
        return self.head

class Solution:
    head = None
    tail = None
    
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        
        def inorder(node):
            if not node: return
            
            inorder(node.left)
            
            # center inorder meat
            # focus on the 1<->2 relationship

            print(node.val)
            
            if not self.head: # or self.tail, new
                self.head = node
            else: # connect prev<->next
                print(f'{self.tail.val}<-{node.val}')
                node.left = self.tail
                print(f'{self.tail.val}->{node.val}')
                self.tail.right = node

            self.tail = node # set prev
            print(f'tail={node.val}')
                    
            inorder(node.right)
                    
        if not root: return
                            
        inorder(root)
                    
        # connect ends head<->tail
        print(f'{self.tail.val}<-{self.head.val}')
        self.head.left = self.tail
        print(f'{self.tail.val}->{self.head.val}')
        self.tail.right = self.head
        
        print(f'head={self.head.val}')
        return self.head

class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        if not root: return None

        self.tail = dum = TreeNode(-1)
        
        def dfs(node):
            if node.left: dfs(node.left) # go all the way left first (1)
            
            # no head/tail check cause we start with dummy tail
            node.left = self.tail
            self.tail.right = node # connect the pred to the current node (dum <-> 1)
            # this same connection also connects the head and tail later

            self.tail = node # think of set tail as predecessor 

            if node.right: dfs(node.right) # then we can go back up and go right (dum <-> 1 <-> 2)
                
        dfs(root)
        
        head = dum.right

        head.left = self.tail # connect head<->tail (1 <-> 5)
        self.tail.right = head

        return head