-
Notifications
You must be signed in to change notification settings - Fork 128
faster int sqrt #328
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
faster int sqrt #328
Conversation
|
Hi @leviska good idea. We put some effort into this in last year's GSoC, but have not put it into Boost yet. We will definitely take a look at your work. The timing looks impresive for hundreds and thousands of bits --- as expected. Very good. I just fired up the CI process and approved your run on CI. So let's see how this goes. It might take a while to negotiate all the details of this thing, but it is in the direction that I think makes sense. Let's give it a whirl in CI. |
|
I am also sure John will be interested in this activity, as we also are. |
|
This is really cool - many thanks! I'll investigate in more detail when I've finished some bug quashing! |
|
Hi @leviska you might find this hard to believe, but i think some of the failures in CI are due to a small artifact in your kara sqrt implementation. In this line, you do not initialize the variable I think it might help to try to modify the line like: |
|
hi, yes, I saw that CI failed and will try to fix it in a few days |
|
Ok, so it seems that I've fixed one of the bugs and some linting things, but there is one thing that I didn't fix Some compilers (clang only???) doesn't have constexpr std::sqrt, so I wanted to replace it with just karatsuba for constexpr version I found __builtin_is_constant_evaluated function, that can help me with that, but it needs to be put accurately, so I'll wait for CI/CD to finish, see what compilers and versions are missing this, and try to fix it for them Also, if there is some define for this builtin I would be glad, if you pointed me to it :) |
|
Actually I think it's only gcc that has a constexpr sqrt at present. There is a macro |
|
It seems that I've fixed basic checks, can you run additional workflows, please? :) Also if you have any review suggestions, I'm open to them |
|
Running GHA now. |
|
It looks like you have added a base-case square root for small bit counts that is actually capable of C++20 That is the right way to go. As this progresses, there is probably a more efficient version thereof that handles more bits and might improve efficiency. Let's see how this goes and we can as a next step get a fast basecase square root. |
| template <class Integer> | ||
| BOOST_MP_CXX14_CONSTEXPR typename std::enable_if<boost::multiprecision::detail::is_integral<Integer>::value, Integer>::type sqrt(const Integer& x, Integer& r) | ||
| { | ||
| if (x == Integer(0)) { |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Minor point, these casts shouldn't be needed (and might actually be expensive), you could probably rewrite as:
if(x.is_zero()){
r = 0u;
return 0u;
}
| else | ||
| #endif | ||
| // we can calculate it faster with std::sqrt | ||
| if (bits <= 64) { |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
If you felt so inclined to do so... it might pay to check which is fastest here:
- double precision sqrt and 53 bits.
- long double and 64 bits, but now using the old x87 co-processor.
- __float128 and 113 bits (when supported).
There is also an assumption here that long double has a 64-bit mantissa, but 53 and 113 bit mantissa's are also common as I'm sure you know.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Might it make sense to check? :
if(bits <= std::numeric_limits<double>::digits)
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
... and then use sqrt from <cmath> if that is your inclination for base-case square root?
| --g; | ||
| } while (g >= 0); | ||
| // https://hal.inria.fr/file/index/docid/72854/filename/RR-3805.pdf | ||
| size_t b = bits / 4; |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
OK, your friendly curmudgeon here ;)
One of the things we found when implementing Karatsuba multiplication was that variable/temporary control was critical to performance. I count at least 7 temporaries here, I admit it would make the code less neat, but some variable reuse would be a good thing. This won't make much difference for fixed-precision cpp_int's, but for variable precision case, it saves a bunch of memory allocations.
The other thing we did - and this is very cpp_int specific - was to figure out up front how much memory would be required for all the variables used in the algorithm (right through all the recursions), and allocate that up front, then share it up between the variables in each recursion. See
| // There are 2 entry point routines for Karatsuba multiplication: |
However, I do appreciate this is already a noticeable improvement, so if you've had enough for now, that's fair enough frankly!
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I also forgot to say.... THANK YOU for this, it's much needed for sure.
|
also, some checks failed, but I'm not sure, is this my fault, or not? there's something about bin_float, and I'm a little confused |
Sigh... only sort of, something, maybe your changes or not, has pushed the size of those object files over the limit msvc can cope with, ignore those for now, I'll look at them tomorrow. |
|
Ok, so I've sped up the code a bit Some more info:
Also I have a question about I thought about float128, and I think I will skip it, because I don't know about it too much (is there even an instruction/function for sqrt(floa128)?). I left the 64 bits there, but I'll try to experiment with it, because as I just found out you can directly cast cpp_int to double, so this "while" algo can be good even for bigger numbers may be? I can't write |
|
Hi, do you have any feedback yet? 👀 |
Sorry about that. I did not notice that we need to approve the run in CI, which I have just approved and CI is running at the time of writing this post. Thanks for pointing this out. Let's see how CI runs. This is an interesting case involving a function that is very interesting for Multiprecision and sought after. Yet shakes the foundation of the architecture, as integer suare root is widely used in multiprecision integer, rational, float and complex. We should see how CI runs, then see what John thinks. If CI passes, we tend to trust our CI testing rather well. If CI testing turns out to be incomplete, we improve CI testing. Maybe we could also run some dedicated user tests and ensure that everything is also working cleanly in a radically multithreaded environment. We also need to be wary if any problems might creep up on other architectures or in more massive parallelization. As a first step, CI is off to the races... |
|
Other than my previous comments... do we have a Google benchmark before and after? Something like sqrt(2^n-1) for n < 100 < n < 1000. Should be O(N) I think before, and O(ln(N)) now? |
Actually for testing integer sqrt, I would recommend populating the binary digits of the integer fully with pseudo-random numbers when benchmarking. We could test branch vs. 1.76. When testing, one must ensure that the test candidates have enough binary digits to actually reach the expected range of Karatsuba benefit threshold, which also should be investigated where exactly that threshold is. I could write up some benchmark code if that helps. |
|
I have this graph, which is based on this benchmark results https://github.com/leviska/boost-sqrt/blob/main/fin/sqrt.json If you want some other benchmark, I could do it, just tell me the details |
This is very nice. I will study those details more closely. I will also run some spot benchmarks to compare with yours at just a few digit counts for fiexed and also report my findings.
Actually, I do want more --- for many many more digits to verify the sub-quadratic expectation of Karatsuba method. This should really kick in around 10,000 ... 100,000 decimal digits, probably becoming visible around 20,000 digits. I think could you add some points, maybe just for fixed, GMP, 1.76 at 2^15, 2^16, maybe even 2^17 binary digits? I would really like to see the original code rise quadratically and the Karatsuba remain non-quadratic. Maybe choose a table or a non-logarithmic scale for the bes exhibition of this behavior |
|
Ok, so I did one more benchmark with 2^n scale https://pastebin.com/QmWN4weF Some images:
(just noticed, that last size is cropped. It's "131072" bits) |
|
Just starting to work through this, some random observations:
I ran some tests using various std::sqrt implementations, what I'm basically seeing is:
More soon. |
thanks!
oops 😰. Thanks for the fix :)
it tries to convert to
actually, it kinda could be faster, because there is this one line, which allocates unused variable for <64 bits |
Hooks up backend-based version for cpp_int. Also adds simple google-benchmark. From #328.
|
There's a problem with the correction code at the end, but I don't quite see the issue at present, test case is: Which asserts inside the final subtraction because If we use a signed type like cpp_int, then we get a different issue: then the remainder comes out larger than the sqrt. Any ideas? |
|
I've checked this test both with your typedef and with cpp_int using my implementation (that I've commited), and it's all working fine I saw, that you did some stuff to the function in another PR, may be there is a typo somewhere? Or is |
|
OK, here's a self contained test case - I've just cut and pasted your code from this PR for the purpose of the test. Tests fail with unsigned types only: |
|
Ooops, sorry about the copy write declaration on that snippet.... cut and past error :( |
|
I might have found the cause - there's a bug in our existing Karatsuba multiplication - it gets the right values in the limbs but breaks some of the classes internal invariants. Testing the fix now.... |
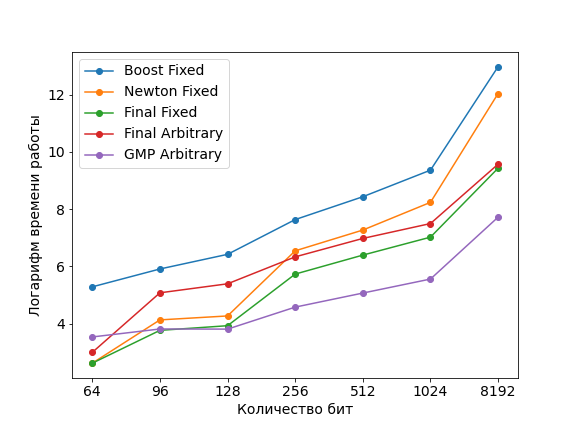
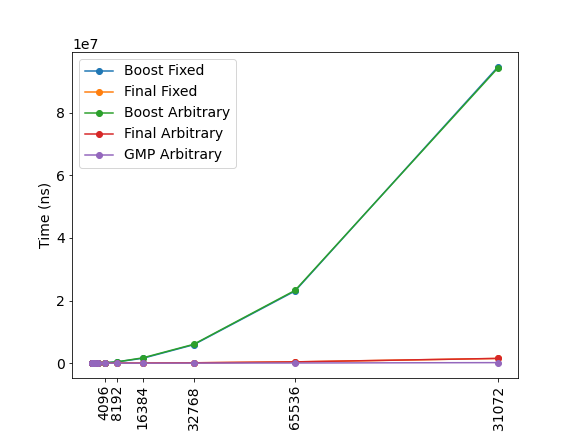
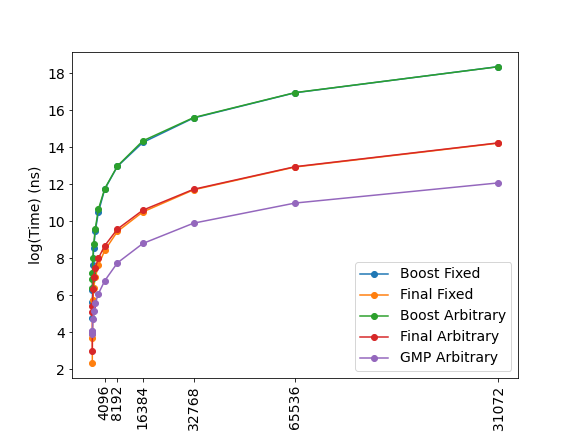
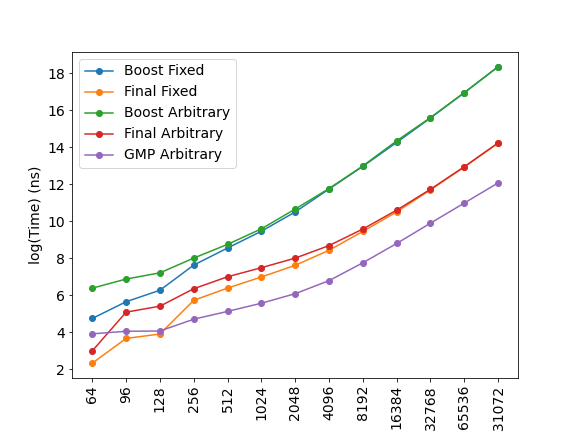
in current implementation of integer sqrt there are lines saying, that it's slow and must be rewritten to karatsuba sqrt method
that's what I did
I've wrote a fast 64 bit sqrt using std::sqrt with correction, because it's simple but still faster, than karatsuba implementation
I've also wrote newton sqrt, but it's kinda the same on small numbers, and much longer on big numbers (probably because of kinda slow multiplication)
also I wrote some tests, because as far as I understood, there was only 1 simple test for checking actual result, not for interfaces, consts and such
a little about motivation:
I could use GMP, but on small (128-256 bits) integers, fixed size cpp_int is way faster, than gmp, so for this kind of numbers it is actually faster to use cpp_int, but the sqrt is too slow, and was taking too much time
on windows, the difference is even worse
some benchmarks, that I run are here (you can find code here https://github.com/leviska/boost-sqrt )
sqrt https://pastebin.com/WvNzVH0g (first number is the size of cpp_int, second is the size of the integer)
operations https://pastebin.com/Tk4mhAfq (you can see, that for 128-256 bit integers cpp_int is actually faster)