-
Notifications
You must be signed in to change notification settings - Fork 16
[fb-survey] Use effective samples size for binary SEs #1065
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Conversation
|
I think we definitely need a couple of unit tests for SE calculations using weighted data, maybe by making up five or ten weights and comparing the result to our documentation. Without that, I'll be nervous. Also, does this PR only change binary indicators, and not the CLI/ILI indicators? Those will also need correct weighting. |
|
Sure, I'll add some tests. CLI/ILI should already match the documentation. Here's the counts indicators code for effective sample size and initial SE and for adjusted SE. I believe it's only binary indicators that haven't been incorporating weights properly. Let me know if I'm misunderstanding something. |
|
Discovered some things. About the docs
About the code
These last two points are causing the test failures, although the absolute difference in implemented and from-the-docs SEs is smallish, O(0.001-0.01). |
|
I'll set aside the documentation points for now, since we should figure out how to fix the code and then ensure all documentation matches it.
It's more than that:
Your link points to
Yes, I think you're right here, and the code needs to match the documentation. |
I agree, but I've already fixed that particular aspect, that is, I've defined regardless of if the estimate is weighted or unweighted. But we should be using (the correct value for) effective sample size instead, right? The implication of this is that historical percentages for binary indicators are wrong. Perhaps we should delete them along with SEs.
The unadjusted formula looks fine, it's the adjustment formula that is inexact. Let me write out the algebra. So starting from the documentation for SE adjustment (minus the typo), But the implemented formula is So there's these two missing terms in the square root,
👍 |
Well... in principle, the Jeffreys adjustment is a hack. We're taking the actual proportion and deliberately fudging it so it can't be 0. A Jeffreys prior is one such way to fudge it, and can be justified by appeal to a Bayesian inference procedure, but there are others. The approach we're using matches the Jeffreys prior in the unweighted case but not in the weighted case. How bad is that? Not too bad, I don't think, as long as the difference between the two approaches is not large and we document it. In fact this current approach does have one advantage: the user can undo it using data in the API, so they can see the actual sample proportion.
Hmmm. How did you arrive at the conclusion that the documented version should not have that The original derivation is documented here: https://github.com/cmu-delphi/covid-19/blob/deeb4dc1e9a30622b415361ef6b99198e77d2a94/facebook/prepare-extracts/aggregations-setup.R#L210-L247 It uses slightly different notation, so let me do it here. Suppose w_i is the weight for observation i, after normalization so they sum to 1. Let y_i be the response for observation i and let \hat \mu be the mean over all observations. Then we have that Now we add a "fake" observation with value 1/2. Working on both sides, Now we solve for the new standard error: Now we see the outline of what's implemented in The remaining question is whether where n_e is defined as in the documentation. Second, it's using as the "old se" instead of the one defined above that correctly accounts for the weights. If we substitute these choices in, what do we get? I dunno, I'm tired, let me finish this later. But evidently I've gone about this a different way than you did. Any idea where we diverged specifically, so we can figure out what's wrong before I finish this off? |
The difference is small (something like O(0.01)) on test data using weights drawn from a uniform distribution; haven't compared with real data. But we are applying the Jeffreys prior using effective sample size for count indicators vs plain sample size for binary indicators, so there's some inconsistency there. Is using raw sample size outright wrong in the weighted case, or is it user's choice and either raw or weighted sample size would be valid (since the adjustment is kind of hacky, like you said)? Are we justified in using plain sample size?
Thanks for linking the derivation, that's helpful. I didn't realize there were different definitions of RE what I think is a typo, Adding more in a separate comment on the derivation you linked. |
|
Okay, I just sent you an invite to an Overleaf document (basically Google Docs for LaTeX, if you haven't used it before) so we can work this out there instead of sharing screenshots of LaTeX snippets. I've written out most of the derivation, with some corrections made for typos and such. So far I'm leaning in the direction that you're right and the code has a typo. But I'd like to write out the derivation in the code in detail and see how, precisely, the two versions differ and where we might have gone wrong in the code; that seems prudent when we don't quite understand how the code got this way, since maybe it's smarter than we are. |
|
Thanks for setting up the doc. I added a derivation in the same vein as the one you linked but assuming that the weights are normalized. |
|
I've updated the Overleaf: I think the difference between code and documentation can be reduced to a simple difference (w0 = 1/neff vs 1/(1 + neff)). Does that look right to you? If so, then we can proceed to deciding which one is more correct. |
|
Yep, looks good! |
|
Made a further update to reorganize the document so it's easy to compare the approaches and understand them. I think that helped me realize a further issue in the documented version that explains why it's different, beyond the choice of w_0. I've added extra explanation. I think the conclusion is that the code is correct and the documentation is wrong. Your definition followed the documentation and started at equation (30), but the code started at equation (19), which is more correct. Or at least it's more correct if you want to add the extra fake weight to both numerator and denominator. Let me know if you agree. |
|
Yes, I agree with your conclusion. The discussion of what The derivations in question, for documentation purposes. |
|
I sent you an invite to another Overleaf doc dealing with the binary case.
We can't do this directly using the explicit |
|
Thanks, the document looks good. I think we can go ahead and implement option 2, and prepare a separate PR to fix the documentation for both binary and count indicators. |
|
And if I understand correctly, all this work led to the conclusion "This PR is correct"? So we just need to prepare the documentation? |
|
(fix the tests) |
clarify comment add uniform tests, increase sample size, correct counts formula update tests new test names
edaa3bf to
f13f9c7
Compare
|
And derivation/discussion for binary indicators This PR isn't quite done, I still need to repair the integration tests. |
|
@capnrefsmmat This is ready to review. |
 capnrefsmmat
left a comment
capnrefsmmat
left a comment
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Looking good. Let's plan to deploy this the week of Nov 30, and figure out a backfill plan with Katie to begin that week.
Mix respondent weights for all indicators
|
Wait for #1397 to be merged. |
|
@krivard This is ready to merge. Since the CTIS API and contingency table pipelines are turned off at this point, this will be used for regenerating/backfilling data with the new, corrected SE definition. |
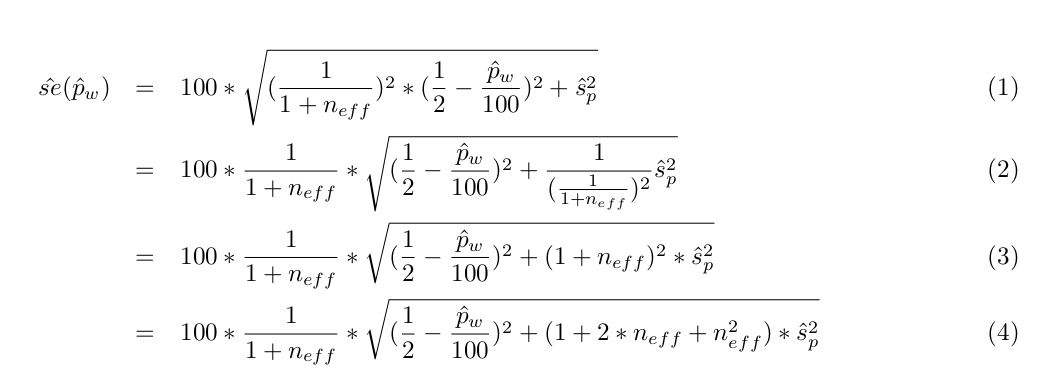
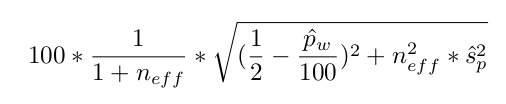
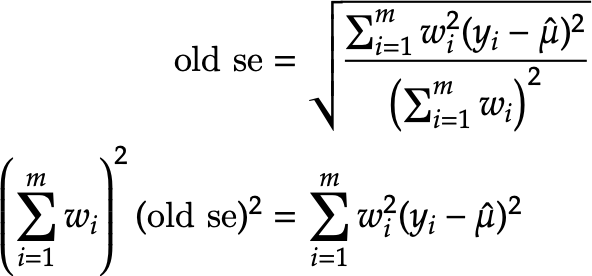
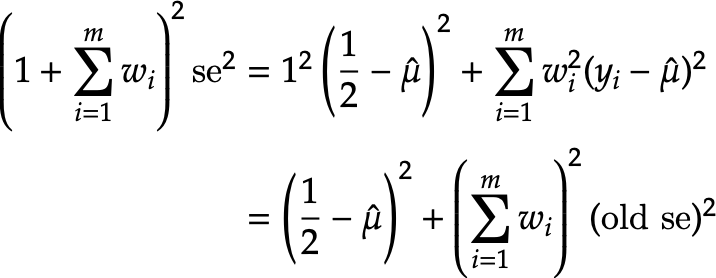
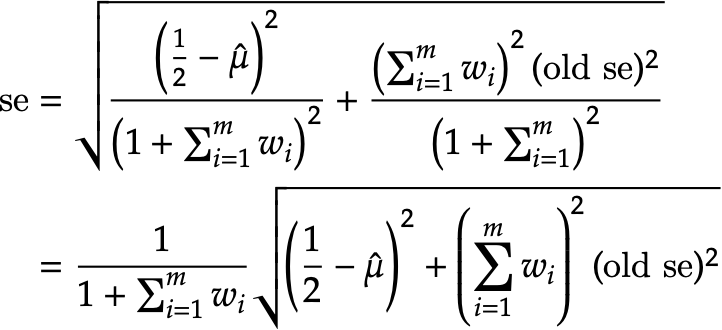
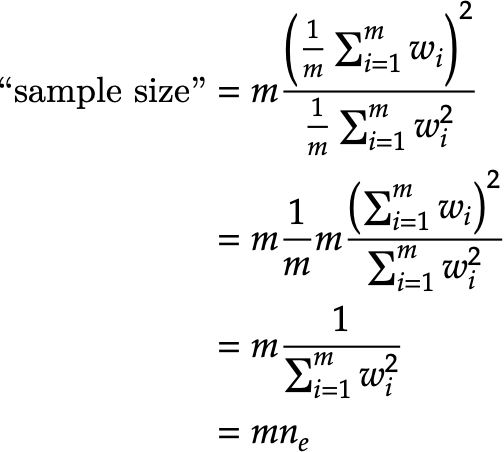
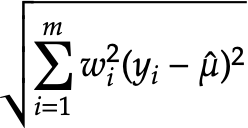

Description
Documented and actual calculations disagree on use of weights in
binary.Rstandard errors. Define and use effective sample size (corresponding to respondent weights) instead of raw sample size (corresponding to uniform weights).Changelog
1/sum(w_i^2), which equals raw sample size when using uniform weights.gold_receivingfiles.Fixes
Code changes for #1271.