Floating Point Numbers
There are two major approaches to store real numbers (i.e., numbers with fractional component) in modern computing. These are
(i) Fixed Point Notation
(ii) Floating Point Notation.
This representation does not reserve a specific number of bits for the integer part or the fractional part.
Single-Precision floating-point number occupies 32-bits, so there is a compromise between the size of the mantissa and the size of the exponent.
- Gaming: Real-time games require high precision and accuracy in the simulation of physics and other complex systems. Floating point numbers are used to calculate the movements and interactions of game objects, as well as to create realistic animations and special effects.
- Machine learning: Machine learning algorithms often require large amounts of data and complex calculations. Floating point numbers are used to ensure precise and accurate computations in applications such as deep learning, natural language processing, and image recognition.
- Computer graphics: Computer graphics require high precision and accuracy to create realistic and visually appealing images. Floating point numbers are used to calculate the position, orientation, and lighting of objects in 3D space.
The exponent is too large to be represented in the Exponent field
The number is too small to be represented in the Exponent fieldTo reduce the chances of underflow/overflow, can use 64-bit Double-Precision arithmetic.
we have 3 elements in a 32-bit floating point representation:
i) Sign
ii) Exponent
iii) Mantissa
IEEE (Institute of Electrical and Electronics Engineers) has standardized Floating-Point Representation
So, actual number is (-1)^s*(1.m)*2(e-Bias) (implicit), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number.
The number of bits assigned to each component depends on the precision of the floating-point format.
According to IEEE 754 standard, the floating-point number is represented in following ways:
Half Precision (16 bit): 1 sign bit, 5 bit exponent, and 10 bit mantissa
Single Precision (32 bit): 1 sign bit, 8 bit exponent, and 23 bit mantissa
Double Precision (64 bit): 1 sign bit, 11 bit exponent, and 52 bit mantissa
Quadruple Precision (128 bit): 1 sign bit, 15 bit exponent, and 112 bit mantissa.
For n bits: (-2)^(n-1) to 2^(n-1) - 1
Say n=4, range of signed bits is:
-2^(4-1) to 2^(4-1) -1
-2^3 to (2^3) -1
-8 to +7
| Signed Number | Binary Format |
|---|---|
| 0 | 0000 |
| +1 | 0001 |
| +2 | 0010 |
| +3 | 0011 |
| +4 | 0100 |
| +5 | 0101 |
| +6 | 0110 |
| +7 | 0111 |
| -8 | 1000 |
| -7 | 1001 |
| -6 | 1010 |
| -5 | 1011 |
| -4 | 1100 |
| -3 | 1101 |
| -2 | 1110 |
| -1 | 1111 |
Here the MSB is the sign bit.
If MSB is 0 then it is a positive number.
If MSB is 1 then it is a negative number.
When MSB=0 the next bits represents the value
When MSB=1 take the 2's complement of the next bits.
Let us consider 1100
MSB = 1 (Number is negative so take 2's complement of the next bits.)
2's complement of 100 is (011+1) = 100
So 1100 = -4
For n Bit Number, range of signed numbers :
-2^(n-1) to 2^(n-1)-1
Two Types:
1)Explicit Normalization:
Move the radix point to the LHS of the most significant '1' in the bit sequence.
It should be in the form of 0.X
(101.101)subscript2 = 0.101101 x 2^3
For example let us consider that we want to represent the above number in 32 bits.
Since it is 32 bits, there will be 1 sign bit, 8 bit exponent, and 23 bit mantissa
Range of signed numbers if you have n bits: (-2^(n-1) to 2^(n-1)-1)
here Exponent should be represented by 8 bits so using 8 bits we can represent from -128 to 127 .
For normalizing we have to add 128.
(101.101)subscript2 = 0.101101 x 2^3
since the number is positive sign bit will be 0.
Add 128 to the exponent
Exponent will be 3+128=131 in binary it will be 10000011
Mantisa will be 101101
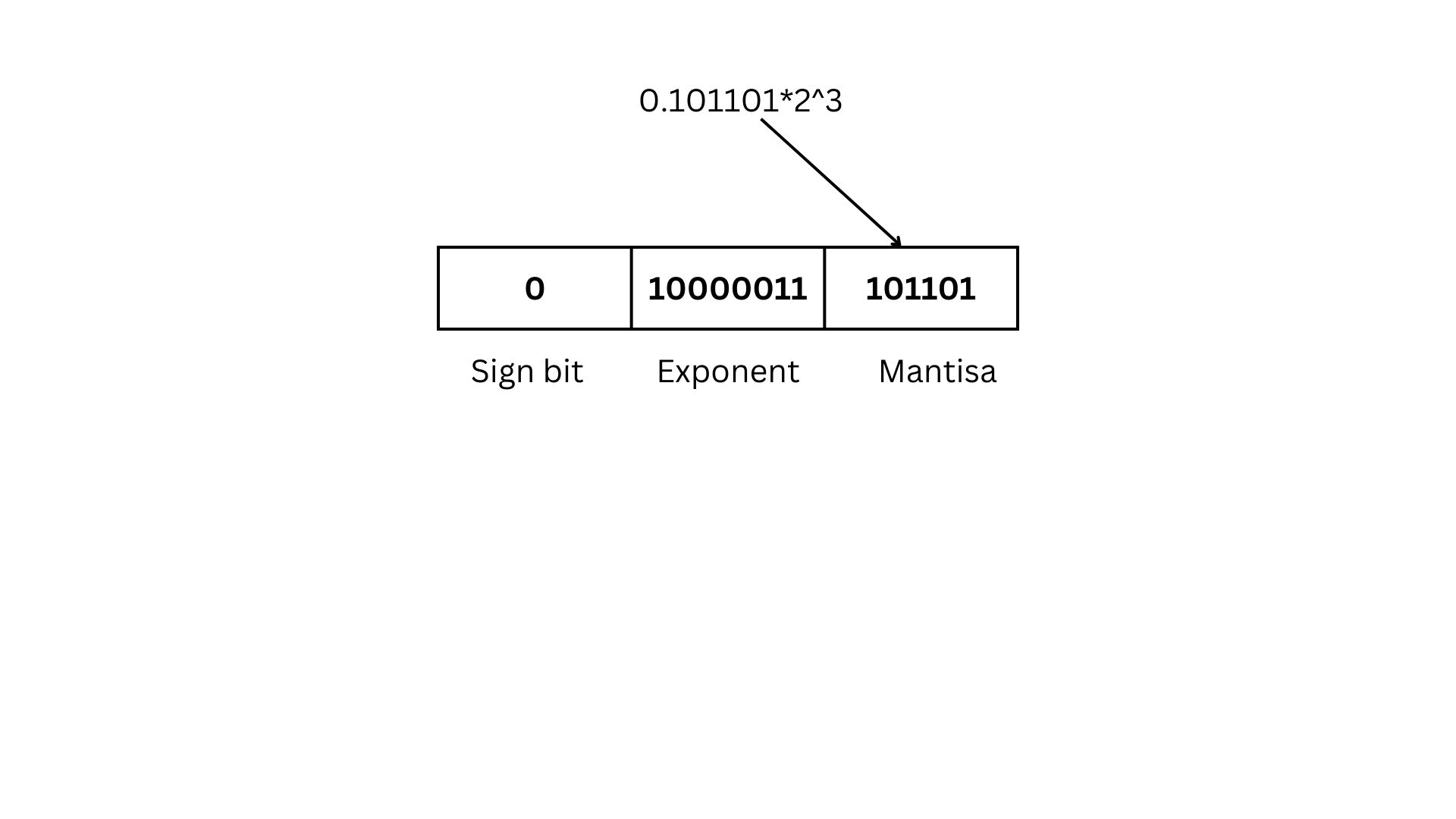
(-1)^s*(0.M)*2^(E-B)
Sign bit is 0
M is mantissa which is 101101
Exponent is 131
Bias is 128
(-1)^0*(0.101101)*2^(131-128) = 0.101101 x 2^3
2)Implicit Normalization: Move the radix point to the RHS of the most significant '1' in the bit sequence.
It should be in the form of 1.X
Consider the example (101.101)subscript2 = 1.01101 x 2^2
For example let us consider that we want to represent the above number in 32 bits.
Since it is 32 bits, there will be 1 sign bit, 8 bit exponent, and 23 bit mantissa
Range of signed numbers if you have n bits: (-2^(n-1) to 2^(n-1)-1)
here Exponent should be represented by 8 bits so using 8 bits we can represent from -128 to 127 .
For normalizing we have to add 128.
(101.101)subscript2 = 1.01101 x 2^2
since the number is positive sign bit will be 0.
Add 128 to the exponent
Exponent will be 2+128=130 in binary it will be 10000010
Mantisa will be 01101
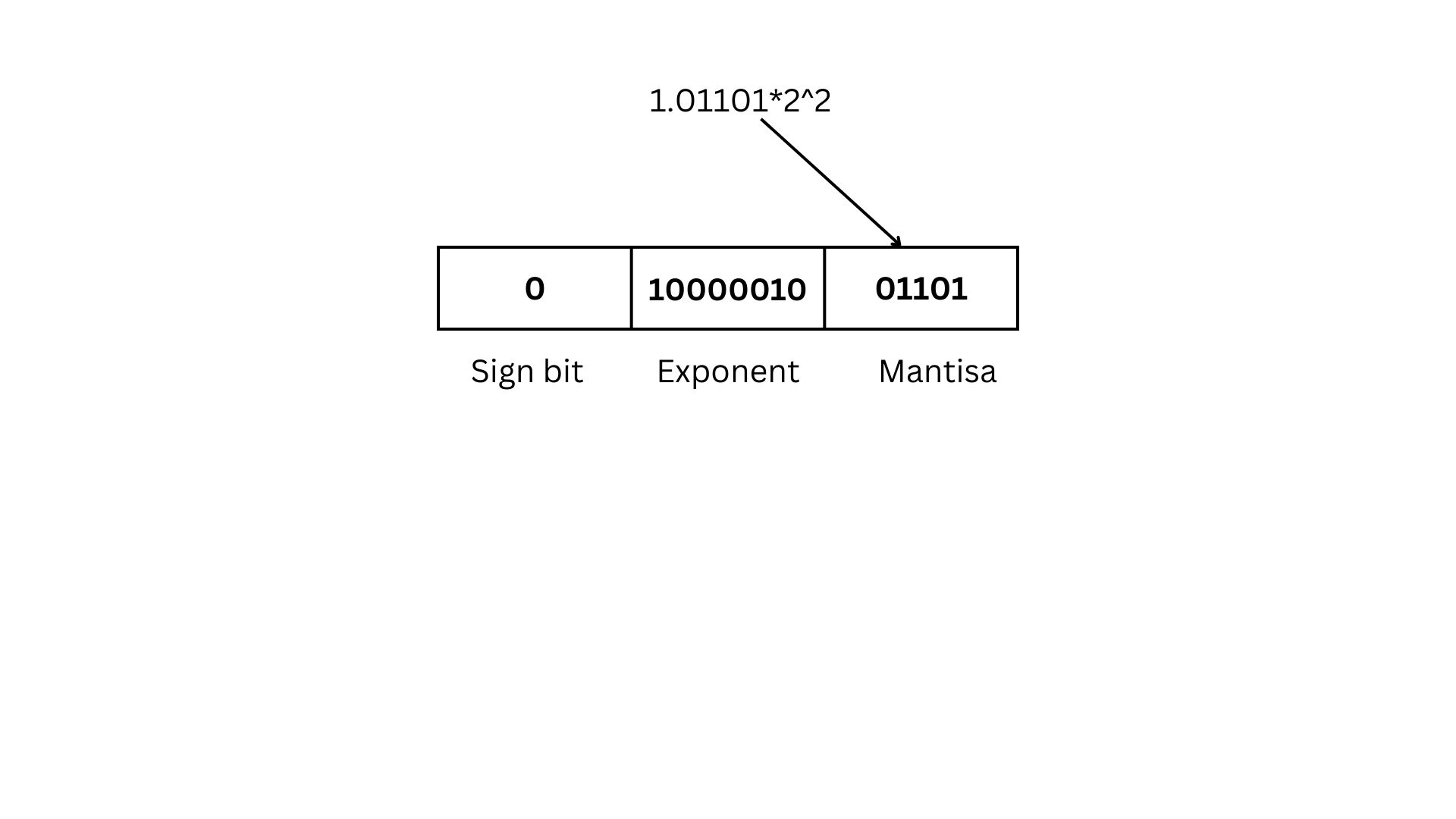
(-1)^s*(1.M)*2^(E-B)
Sign bit is 0
M is mantissa which is 01101
Exponent is 130
Bias is 128
(-1)^0*(1.01101)*2^(130-128) = 0.101101 x 2^2
First we will convert 10^15
2^x=10^15
Taking log on both sides
log(2^x)=log(10^15)
xlog2=15log10 log2=0.3 and log10=1
0.3x=15
x=15*10/0.3*10
x=50
so 2^50=10^15
-(1.75)*10^15 in decimal = -(1.11)*2^50 in binary
Since the number is negative Sign bit will be 1. (1 bit)
Exponent is 50+128=178 , in binary it will be 10110010 (8 bit)
Mantisa =1100000000.....00 (23 bit)
For the same above example
Implicit normalization is more precise than the Explicit normalization.
- A 10-bit format would not provide much precision relative to the range of values that could be represented.
- The existing hardware and software implementations of floating-point arithmetic are optimized for 32-bit and 64-bit formats.
- "Cell Library" is not available for 10 bit formats.
- Supporting a 10-bit format would require significant changes to the hardware and software, which would be costly and time-consuming.
- There may not be a compelling use case for a 10-bit floating-point format, most applications that require floating-point arithmetic can be adequately served by existing formats, and the benefits of a 10-bit format may not justify the cost and complexity of introducing a new format.
A floating-point unit (FPU, colloquially a math coprocessor) is a part of a computer system
specially designed to carry out operations on floating-point numbers.
Typical operations are addition, subtraction, multiplication, division, and square root.
Image result for what is floating point unit in digital electronics
Floating point numbers are used to represent noninteger fractional numbers and are used in most engineering and technical calculations,
for example, 3.256, 2.1, and 0.0036. The most commonly used floating point standard is the IEEE standard.
A floating-point unit (FPU, colloquially a math coprocessor) is a part of a computer system
specially designed to carry out operations on floating-point numbers.
Typical operations are addition, subtraction, multiplication, division, and square root.
Image result for what is floating point unit in digital electronics
Floating point numbers are used to represent noninteger fractional numbers and are used in most engineering and technical calculations,
for example, 3.256, 2.1, and 0.0036. The most commonly used floating point standard is the IEEE standard.